The Rényi Gaussian Process
Paper and Code
Oct 17, 2019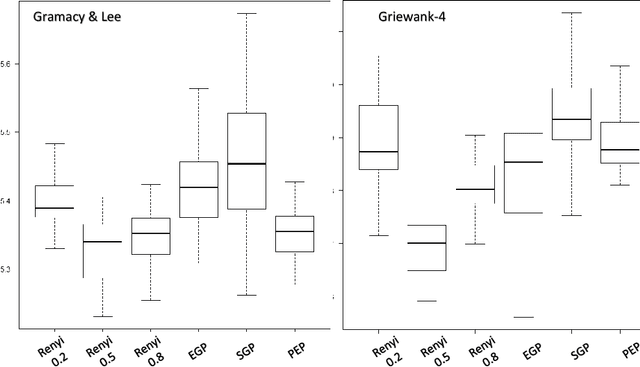
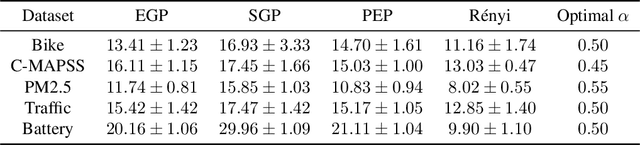
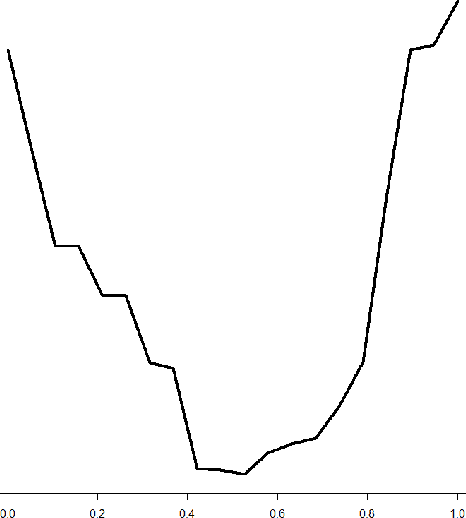
In this article we introduce an alternative closed form lower bound on the Gaussian process ($\mathcal{GP}$) likelihood based on the R\'enyi $\alpha$-divergence. This new lower bound can be viewed as a convex combination of the Nystr\"om approximation and the exact $\mathcal{GP}$. The key advantage of this bound, is its capability to control and tune the enforced regularization on the model and thus is a generalization of the traditional sparse variational $\mathcal{GP}$ regression. From the theoretical perspective, we show that with probability at least $1-\delta$, the R\'enyi $\alpha$-divergence between the variational distribution and the true posterior becomes arbitrarily small as the number of data points increase.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge