Personalized Tucker Decomposition: Modeling Commonality and Peculiarity on Tensor Data

We propose personalized Tucker decomposition (perTucker) to address the limitations of traditional tensor decomposition methods in capturing heterogeneity across different datasets. perTucker decomposes tensor data into shared global components and personalized local components. We introduce a mode orthogonality assumption and develop a proximal gradient regularized block coordinate descent algorithm that is guaranteed to converge to a stationary point. By learning unique and common representations across datasets, we demonstrate perTucker's effectiveness in anomaly detection, client classification, and clustering through a simulation study and two case studies on solar flare detection and tonnage signal classification.

Personalized Dictionary Learning for Heterogeneous Datasets

We introduce a relevant yet challenging problem named Personalized Dictionary Learning (PerDL), where the goal is to learn sparse linear representations from heterogeneous datasets that share some commonality. In PerDL, we model each dataset's shared and unique features as global and local dictionaries. Challenges for PerDL not only are inherited from classical dictionary learning (DL), but also arise due to the unknown nature of the shared and unique features. In this paper, we rigorously formulate this problem and provide conditions under which the global and local dictionaries can be provably disentangled. Under these conditions, we provide a meta-algorithm called Personalized Matching and Averaging (PerMA) that can recover both global and local dictionaries from heterogeneous datasets. PerMA is highly efficient; it converges to the ground truth at a linear rate under suitable conditions. Moreover, it automatically borrows strength from strong learners to improve the prediction of weak learners. As a general framework for extracting global and local dictionaries, we show the application of PerDL in different learning tasks, such as training with imbalanced datasets and video surveillance.

Adam Can Converge Without Any Modification on Update Rules

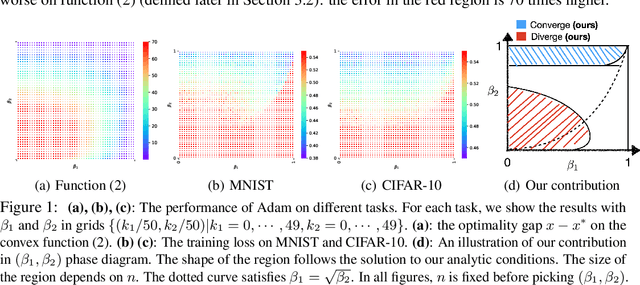
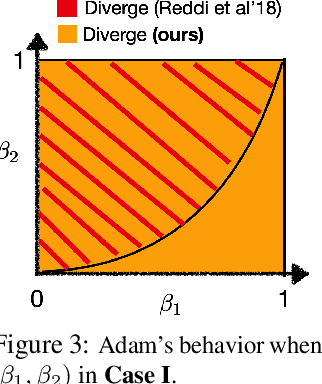
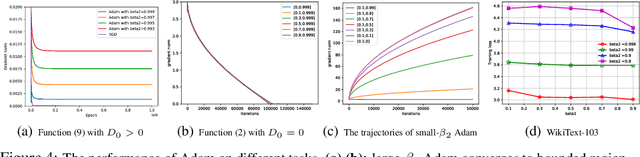
Ever since Reddi et al. 2018 pointed out the divergence issue of Adam, many new variants have been designed to obtain convergence. However, vanilla Adam remains exceptionally popular and it works well in practice. Why is there a gap between theory and practice? We point out there is a mismatch between the settings of theory and practice: Reddi et al. 2018 pick the problem after picking the hyperparameters of Adam, i.e., $(\beta_1, \beta_2)$; while practical applications often fix the problem first and then tune $(\beta_1, \beta_2)$. Due to this observation, we conjecture that the empirical convergence can be theoretically justified, only if we change the order of picking the problem and hyperparameter. In this work, we confirm this conjecture. We prove that, when $\beta_2$ is large and $\beta_1 < \sqrt{\beta_2}<1$, Adam converges to the neighborhood of critical points. The size of the neighborhood is propositional to the variance of stochastic gradients. Under an extra condition (strong growth condition), Adam converges to critical points. As $\beta_2$ increases, our convergence result can cover any $\beta_1 \in [0,1)$ including $\beta_1=0.9$, which is the default setting in deep learning libraries. To our knowledge, this is the first result showing that Adam can converge under a wide range of hyperparameters {\it without any modification} on its update rules. Further, our analysis does not require assumptions of bounded gradients or bounded 2nd-order momentum. When $\beta_2$ is small, we further point out a large region of $(\beta_1,\beta_2)$ where Adam can diverge to infinity. Our divergence result considers the same setting as our convergence result, indicating a phase transition from divergence to convergence when increasing $\beta_2$. These positive and negative results can provide suggestions on how to tune Adam hyperparameters.

Personalized PCA: Decoupling Shared and Unique Features

In this paper, we tackle a significant challenge in PCA: heterogeneity. When data are collected from different sources with heterogeneous trends while still sharing some congruency, it is critical to extract shared knowledge while retaining unique features of each source. To this end, we propose personalized PCA (PerPCA), which uses mutually orthogonal global and local principal components to encode both unique and shared features. We show that, under mild conditions, both unique and shared features can be identified and recovered by a constrained optimization problem, even if the covariance matrices are immensely different. Also, we design a fully federated algorithm inspired by distributed Stiefel gradient descent to solve the problem. The algorithm introduces a new group of operations called generalized retractions to handle orthogonality constraints, and only requires global PCs to be shared across sources. We prove the linear convergence of the algorithm under suitable assumptions. Comprehensive numerical experiments highlight PerPCA's superior performance in feature extraction and prediction from heterogeneous datasets. As a systematic approach to decouple shared and unique features from heterogeneous datasets, PerPCA finds applications in several tasks including video segmentation, topic extraction, and distributed clustering.

The Internet of Federated Things : A Vision for the Future and In-depth Survey of Data-driven Approaches for Federated Learning

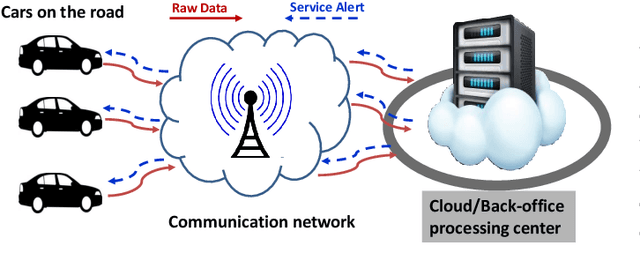
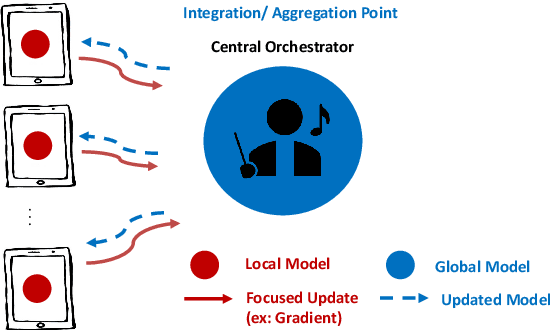
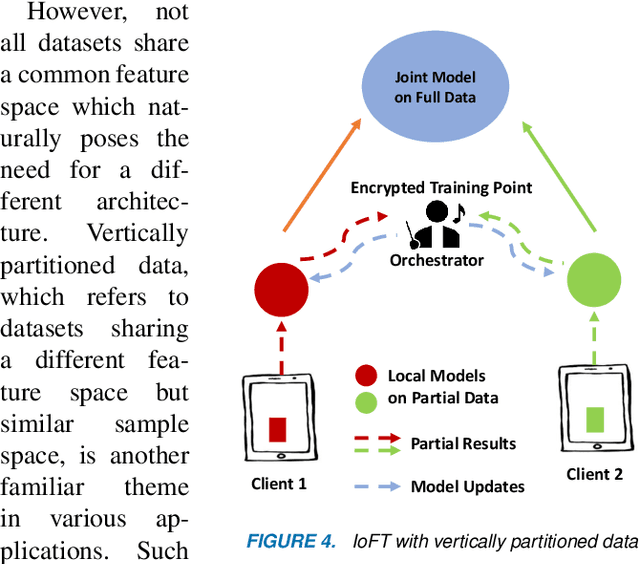
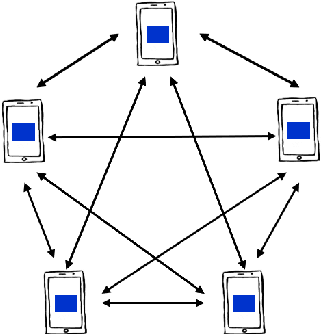
The Internet of Things (IoT) is on the verge of a major paradigm shift. In the IoT system of the future, IoFT, the cloud will be substituted by the crowd where model training is brought to the edge, allowing IoT devices to collaboratively extract knowledge and build smart analytics/models while keeping their personal data stored locally. This paradigm shift was set into motion by the tremendous increase in computational power on IoT devices and the recent advances in decentralized and privacy-preserving model training, coined as federated learning (FL). This article provides a vision for IoFT and a systematic overview of current efforts towards realizing this vision. Specifically, we first introduce the defining characteristics of IoFT and discuss FL data-driven approaches, opportunities, and challenges that allow decentralized inference within three dimensions: (i) a global model that maximizes utility across all IoT devices, (ii) a personalized model that borrows strengths across all devices yet retains its own model, (iii) a meta-learning model that quickly adapts to new devices or learning tasks. We end by describing the vision and challenges of IoFT in reshaping different industries through the lens of domain experts. Those industries include manufacturing, transportation, energy, healthcare, quality & reliability, business, and computing.

Fed-ensemble: Improving Generalization through Model Ensembling in Federated Learning

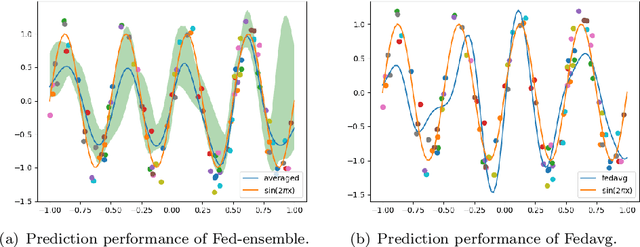
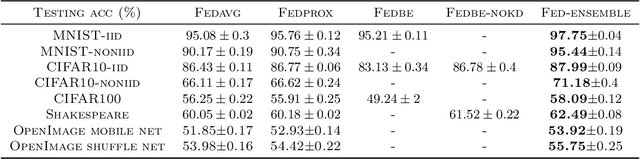
In this paper we propose Fed-ensemble: a simple approach that bringsmodel ensembling to federated learning (FL). Instead of aggregating localmodels to update a single global model, Fed-ensemble uses random permutations to update a group of K models and then obtains predictions through model averaging. Fed-ensemble can be readily utilized within established FL methods and does not impose a computational overhead as it only requires one of the K models to be sent to a client in each communication round. Theoretically, we show that predictions on newdata from all K models belong to the same predictive posterior distribution under a neural tangent kernel regime. This result in turn sheds light onthe generalization advantages of model averaging. We also illustrate thatFed-ensemble has an elegant Bayesian interpretation. Empirical results show that our model has superior performance over several FL algorithms,on a wide range of data sets, and excels in heterogeneous settings often encountered in FL applications.

ScrofaZero: Mastering Trick-taking Poker Game Gongzhu by Deep Reinforcement Learning

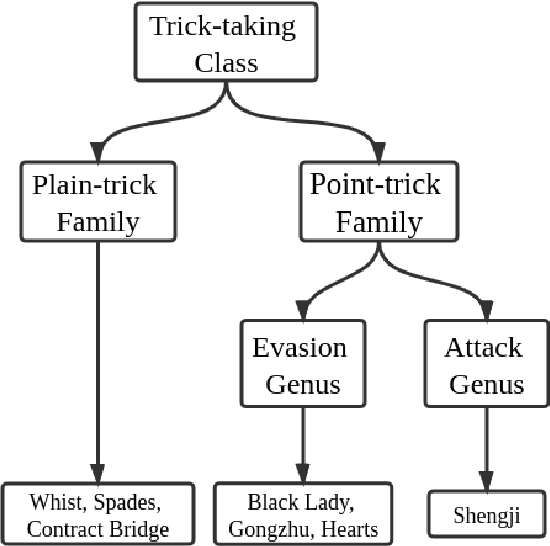
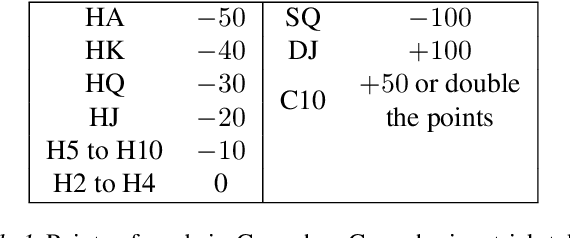
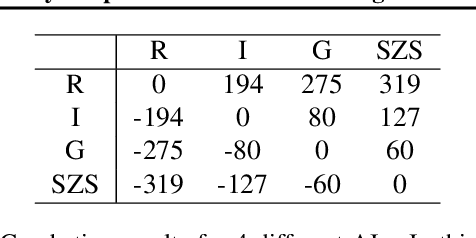
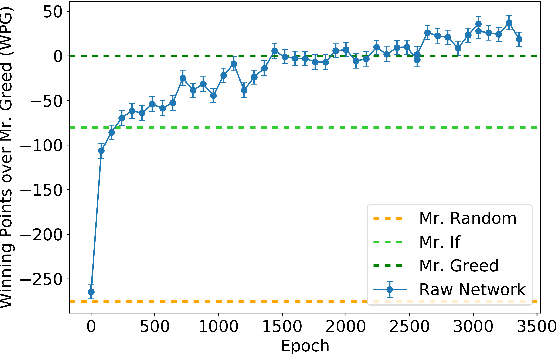
People have made remarkable progress in game AIs, especially in domain of perfect information game. However, trick-taking poker game, as a popular form of imperfect information game, has been regarded as a challenge for a long time. Since trick-taking game requires high level of not only reasoning, but also inference to excel, it can be a new milestone for imperfect information game AI. We study Gongzhu, a trick-taking game analogous to, but slightly simpler than contract bridge. Nonetheless, the strategies of Gongzhu are complex enough for both human and computer players. We train a strong Gongzhu AI ScrofaZero from \textit{tabula rasa} by deep reinforcement learning, while few previous efforts on solving trick-taking poker game utilize the representation power of neural networks. Also, we introduce new techniques for imperfect information game including stratified sampling, importance weighting, integral over equivalent class, Bayesian inference, etc. Our AI can achieve human expert level performance. The methodologies in building our program can be easily transferred into a wide range of trick-taking games.