Salar Fattahi
Implicit Regularization of Infinitesimally-perturbed Gradient Descent Toward Low-dimensional Solutions
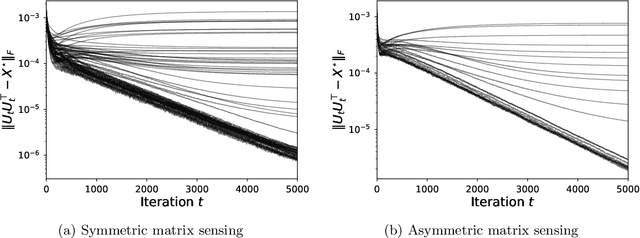
May 22, 2025Abstract:Implicit regularization refers to the phenomenon where local search algorithms converge to low-dimensional solutions, even when such structures are neither explicitly specified nor encoded in the optimization problem. While widely observed, this phenomenon remains theoretically underexplored, particularly in modern over-parameterized problems. In this paper, we study the conditions that enable implicit regularization by investigating when gradient-based methods converge to second-order stationary points (SOSPs) within an implicit low-dimensional region of a smooth, possibly nonconvex function. We show that successful implicit regularization hinges on two key conditions: $(i)$ the ability to efficiently escape strict saddle points, while $(ii)$ maintaining proximity to the implicit region. Existing analyses enabling the convergence of gradient descent (GD) to SOSPs often rely on injecting large perturbations to escape strict saddle points. However, this comes at the cost of deviating from the implicit region. The central premise of this paper is that it is possible to achieve the best of both worlds: efficiently escaping strict saddle points using infinitesimal perturbations, while controlling deviation from the implicit region via a small deviation rate. We show that infinitesimally perturbed gradient descent (IPGD), which can be interpreted as GD with inherent ``round-off errors'', can provably satisfy both conditions. We apply our framework to the problem of over-parameterized matrix sensing, where we establish formal guarantees for the implicit regularization behavior of IPGD. We further demonstrate through extensive experiments that these insights extend to a broader class of learning problems.
RANSAC Revisited: An Improved Algorithm for Robust Subspace Recovery under Adversarial and Noisy Corruptions
Apr 13, 2025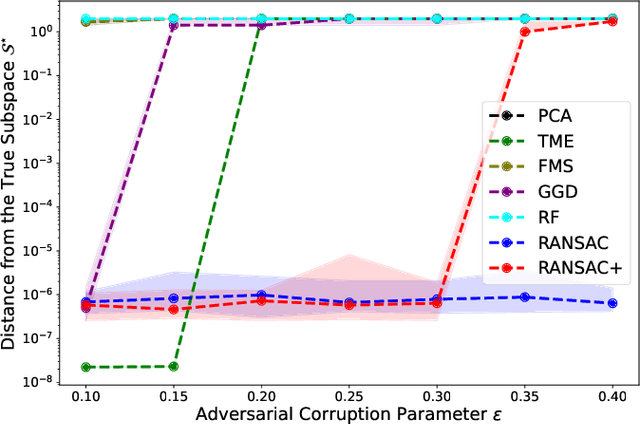
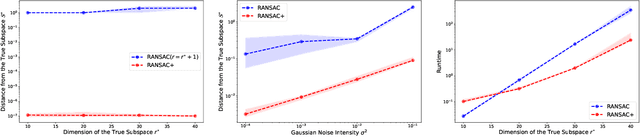
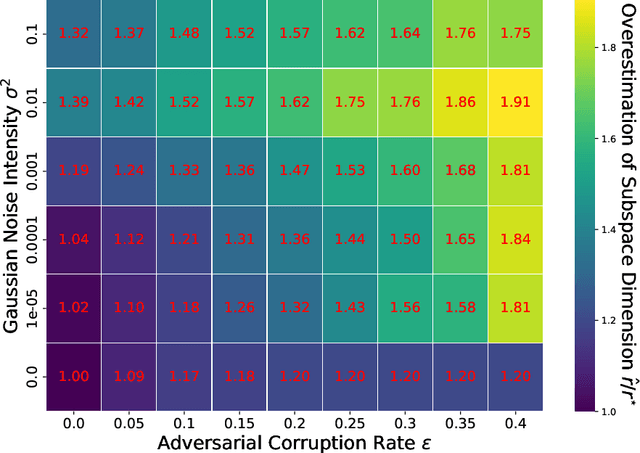
Abstract:In this paper, we study the problem of robust subspace recovery (RSR) in the presence of both strong adversarial corruptions and Gaussian noise. Specifically, given a limited number of noisy samples -- some of which are tampered by an adaptive and strong adversary -- we aim to recover a low-dimensional subspace that approximately contains a significant fraction of the uncorrupted samples, up to an error that scales with the Gaussian noise. Existing approaches to this problem often suffer from high computational costs or rely on restrictive distributional assumptions, limiting their applicability in truly adversarial settings. To address these challenges, we revisit the classical random sample consensus (RANSAC) algorithm, which offers strong robustness to adversarial outliers, but sacrifices efficiency and robustness against Gaussian noise and model misspecification in the process. We propose a two-stage algorithm, RANSAC+, that precisely pinpoints and remedies the failure modes of standard RANSAC. Our method is provably robust to both Gaussian and adversarial corruptions, achieves near-optimal sample complexity without requiring prior knowledge of the subspace dimension, and is more efficient than existing RANSAC-type methods.
Preconditioned Gradient Descent for Over-Parameterized Nonconvex Matrix Factorization
Apr 13, 2025Abstract:In practical instances of nonconvex matrix factorization, the rank of the true solution $r^{\star}$ is often unknown, so the rank $r$ of the model can be overspecified as $r>r^{\star}$. This over-parameterized regime of matrix factorization significantly slows down the convergence of local search algorithms, from a linear rate with $r=r^{\star}$ to a sublinear rate when $r>r^{\star}$. We propose an inexpensive preconditioner for the matrix sensing variant of nonconvex matrix factorization that restores the convergence rate of gradient descent back to linear, even in the over-parameterized case, while also making it agnostic to possible ill-conditioning in the ground truth. Classical gradient descent in a neighborhood of the solution slows down due to the need for the model matrix factor to become singular. Our key result is that this singularity can be corrected by $\ell_{2}$ regularization with a specific range of values for the damping parameter. In fact, a good damping parameter can be inexpensively estimated from the current iterate. The resulting algorithm, which we call preconditioned gradient descent or PrecGD, is stable under noise, and converges linearly to an information theoretically optimal error bound. Our numerical experiments find that PrecGD works equally well in restoring the linear convergence of other variants of nonconvex matrix factorization in the over-parameterized regime.
Enhancing Performance of Explainable AI Models with Constrained Concept Refinement
Feb 10, 2025



Abstract:The trade-off between accuracy and interpretability has long been a challenge in machine learning (ML). This tension is particularly significant for emerging interpretable-by-design methods, which aim to redesign ML algorithms for trustworthy interpretability but often sacrifice accuracy in the process. In this paper, we address this gap by investigating the impact of deviations in concept representations-an essential component of interpretable models-on prediction performance and propose a novel framework to mitigate these effects. The framework builds on the principle of optimizing concept embeddings under constraints that preserve interpretability. Using a generative model as a test-bed, we rigorously prove that our algorithm achieves zero loss while progressively enhancing the interpretability of the resulting model. Additionally, we evaluate the practical performance of our proposed framework in generating explainable predictions for image classification tasks across various benchmarks. Compared to existing explainable methods, our approach not only improves prediction accuracy while preserving model interpretability across various large-scale benchmarks but also achieves this with significantly lower computational cost.
Convergence of Gradient Descent with Small Initialization for Unregularized Matrix Completion
Feb 09, 2024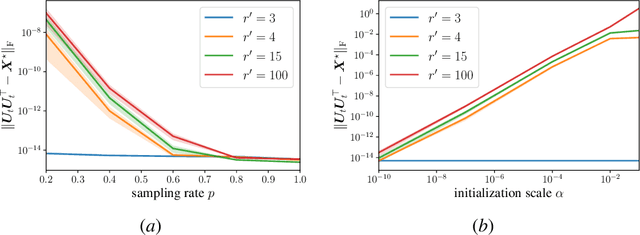

Abstract:We study the problem of symmetric matrix completion, where the goal is to reconstruct a positive semidefinite matrix $\rm{X}^\star \in \mathbb{R}^{d\times d}$ of rank-$r$, parameterized by $\rm{U}\rm{U}^{\top}$, from only a subset of its observed entries. We show that the vanilla gradient descent (GD) with small initialization provably converges to the ground truth $\rm{X}^\star$ without requiring any explicit regularization. This convergence result holds true even in the over-parameterized scenario, where the true rank $r$ is unknown and conservatively over-estimated by a search rank $r'\gg r$. The existing results for this problem either require explicit regularization, a sufficiently accurate initial point, or exact knowledge of the true rank $r$. In the over-parameterized regime where $r'\geq r$, we show that, with $\widetilde\Omega(dr^9)$ observations, GD with an initial point $\|\rm{U}_0\| \leq \epsilon$ converges near-linearly to an $\epsilon$-neighborhood of $\rm{X}^\star$. Consequently, smaller initial points result in increasingly accurate solutions. Surprisingly, neither the convergence rate nor the final accuracy depends on the over-parameterized search rank $r'$, and they are only governed by the true rank $r$. In the exactly-parameterized regime where $r'=r$, we further enhance this result by proving that GD converges at a faster rate to achieve an arbitrarily small accuracy $\epsilon>0$, provided the initial point satisfies $\|\rm{U}_0\| = O(1/d)$. At the crux of our method lies a novel weakly-coupled leave-one-out analysis, which allows us to establish the global convergence of GD, extending beyond what was previously possible using the classical leave-one-out analysis.
Solution Path of Time-varying Markov Random Fields with Discrete Regularization
Jul 25, 2023Abstract:We study the problem of inferring sparse time-varying Markov random fields (MRFs) with different discrete and temporal regularizations on the parameters. Due to the intractability of discrete regularization, most approaches for solving this problem rely on the so-called maximum-likelihood estimation (MLE) with relaxed regularization, which neither results in ideal statistical properties nor scale to the dimensions encountered in realistic settings. In this paper, we address these challenges by departing from the MLE paradigm and resorting to a new class of constrained optimization problems with exact, discrete regularization to promote sparsity in the estimated parameters. Despite the nonconvex and discrete nature of our formulation, we show that it can be solved efficiently and parametrically for all sparsity levels. More specifically, we show that the entire solution path of the time-varying MRF for all sparsity levels can be obtained in $\mathcal{O}(pT^3)$, where $T$ is the number of time steps and $p$ is the number of unknown parameters at any given time. The efficient and parametric characterization of the solution path renders our approach highly suitable for cross-validation, where parameter estimation is required for varying regularization values. Despite its simplicity and efficiency, we show that our proposed approach achieves provably small estimation error for different classes of time-varying MRFs, namely Gaussian and discrete MRFs, with as few as one sample per time. Utilizing our algorithm, we can recover the complete solution path for instances of time-varying MRFs featuring over 30 million variables in less than 12 minutes on a standard laptop computer. Our code is available at \url{https://sites.google.com/usc.edu/gomez/data}.
Robust Sparse Mean Estimation via Incremental Learning
May 24, 2023Abstract:In this paper, we study the problem of robust sparse mean estimation, where the goal is to estimate a $k$-sparse mean from a collection of partially corrupted samples drawn from a heavy-tailed distribution. Existing estimators face two critical challenges in this setting. First, they are limited by a conjectured computational-statistical tradeoff, implying that any computationally efficient algorithm needs $\tilde\Omega(k^2)$ samples, while its statistically-optimal counterpart only requires $\tilde O(k)$ samples. Second, the existing estimators fall short of practical use as they scale poorly with the ambient dimension. This paper presents a simple mean estimator that overcomes both challenges under moderate conditions: it runs in near-linear time and memory (both with respect to the ambient dimension) while requiring only $\tilde O(k)$ samples to recover the true mean. At the core of our method lies an incremental learning phenomenon: we introduce a simple nonconvex framework that can incrementally learn the top-$k$ nonzero elements of the mean while keeping the zero elements arbitrarily small. Unlike existing estimators, our method does not need any prior knowledge of the sparsity level $k$. We prove the optimality of our estimator by providing a matching information-theoretic lower bound. Finally, we conduct a series of simulations to corroborate our theoretical findings. Our code is available at https://github.com/huihui0902/Robust_mean_estimation.
Personalized Dictionary Learning for Heterogeneous Datasets
May 24, 2023Abstract:We introduce a relevant yet challenging problem named Personalized Dictionary Learning (PerDL), where the goal is to learn sparse linear representations from heterogeneous datasets that share some commonality. In PerDL, we model each dataset's shared and unique features as global and local dictionaries. Challenges for PerDL not only are inherited from classical dictionary learning (DL), but also arise due to the unknown nature of the shared and unique features. In this paper, we rigorously formulate this problem and provide conditions under which the global and local dictionaries can be provably disentangled. Under these conditions, we provide a meta-algorithm called Personalized Matching and Averaging (PerMA) that can recover both global and local dictionaries from heterogeneous datasets. PerMA is highly efficient; it converges to the ground truth at a linear rate under suitable conditions. Moreover, it automatically borrows strength from strong learners to improve the prediction of weak learners. As a general framework for extracting global and local dictionaries, we show the application of PerDL in different learning tasks, such as training with imbalanced datasets and video surveillance.
On the Optimization Landscape of Burer-Monteiro Factorization: When do Global Solutions Correspond to Ground Truth?
Feb 21, 2023
Abstract:In low-rank matrix recovery, the goal is to recover a low-rank matrix, given a limited number of linear and possibly noisy measurements. Low-rank matrix recovery is typically solved via a nonconvex method called Burer-Monteiro factorization (BM). If the rank of the ground truth is known, BM is free of sub-optimal local solutions, and its true solutions coincide with the global solutions -- that is, the true solutions are identifiable. When the rank of the ground truth is unknown, it must be over-estimated, giving rise to an over-parameterized BM. In the noiseless regime, it is recently shown that over-estimation of the rank leads to progressively fewer sub-optimal local solutions while preserving the identifiability of the true solutions. In this work, we show that with noisy measurements, the global solutions of the over-parameterized BM no longer correspond to the true solutions, essentially transmuting over-parameterization from blessing to curse. In particular, we study two classes of low-rank matrix recovery, namely matrix completion and matrix sensing. For matrix completion, we show that even if the rank is only slightly over-estimated and with very mild assumptions on the noise, none of the true solutions are local or global solutions. For matrix sensing, we show that to guarantee the correspondence between global and true solutions, it is necessary and sufficient for the number of samples to scale linearly with the over-estimated rank, which can be drastically larger than its optimal sample complexity that only scales with the true rank.
Simple Alternating Minimization Provably Solves Complete Dictionary Learning
Oct 23, 2022Abstract:This paper focuses on complete dictionary learning problem, where the goal is to reparametrize a set of given signals as linear combinations of atoms from a learned dictionary. There are two main challenges faced by theoretical and practical studies of dictionary learning: the lack of theoretical guarantees for practically-used heuristic algorithms, and their poor scalability when dealing with huge-scale datasets. Towards addressing these issues, we show that when the dictionary to be learned is orthogonal, that an alternating minimization method directly applied to the nonconvex and discrete formulation of the problem exactly recovers the ground truth. For the huge-scale, potentially online setting, we propose a minibatch version of our algorithm, which can provably learn a complete dictionary from a huge-scale dataset with minimal sample complexity, linear sparsity level, and linear convergence rate, thereby negating the need for any convex relaxation for the problem. Our numerical experiments showcase the superiority of our method compared with the existing techniques when applied to tasks on real data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge