SDP-CROWN: Efficient Bound Propagation for Neural Network Verification with Tightness of Semidefinite Programming

Neural network verifiers based on linear bound propagation scale impressively to massive models but can be surprisingly loose when neuron coupling is crucial. Conversely, semidefinite programming (SDP) verifiers capture inter-neuron coupling naturally, but their cubic complexity restricts them to only small models. In this paper, we propose SDP-CROWN, a novel hybrid verification framework that combines the tightness of SDP relaxations with the scalability of bound-propagation verifiers. At the core of SDP-CROWN is a new linear bound, derived via SDP principles, that explicitly captures $\ell_{2}$-norm-based inter-neuron coupling while adding only one extra parameter per layer. This bound can be integrated seamlessly into any linear bound-propagation pipeline, preserving the inherent scalability of such methods yet significantly improving tightness. In theory, we prove that our inter-neuron bound can be up to a factor of $\sqrt{n}$ tighter than traditional per-neuron bounds. In practice, when incorporated into the state-of-the-art $\alpha$-CROWN verifier, we observe markedly improved verification performance on large models with up to 65 thousand neurons and 2.47 million parameters, achieving tightness that approaches that of costly SDP-based methods.

Nonnegative Low-rank Matrix Recovery Can Have Spurious Local Minima

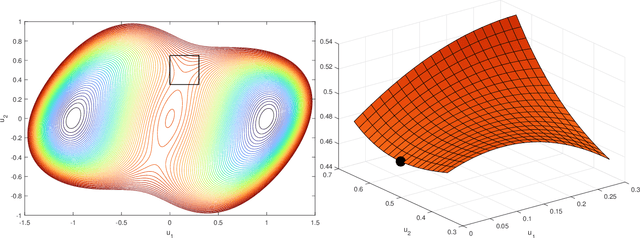
The classical low-rank matrix recovery problem is well-known to exhibit \emph{benign nonconvexity} under the restricted isometry property (RIP): local optimization is guaranteed to converge to the global optimum, where the ground truth is recovered. We investigate whether benign nonconvexity continues to hold when the factor matrices are constrained to be elementwise nonnegative -- a common practical requirement. In the simple setting of a rank-1 nonnegative ground truth, we confirm that benign nonconvexity holds in the fully-observed case with RIP constant $\delta=0$. Surprisingly, however, this property fails to extend to the partially-observed case with any arbitrarily small RIP constant $\delta\to0^{+}$, irrespective of rank overparameterization. This finding exposes a critical theoretical gap: the continuity argument widely used to explain the empirical robustness of low-rank matrix recovery fundamentally breaks down once nonnegative constraints are imposed.

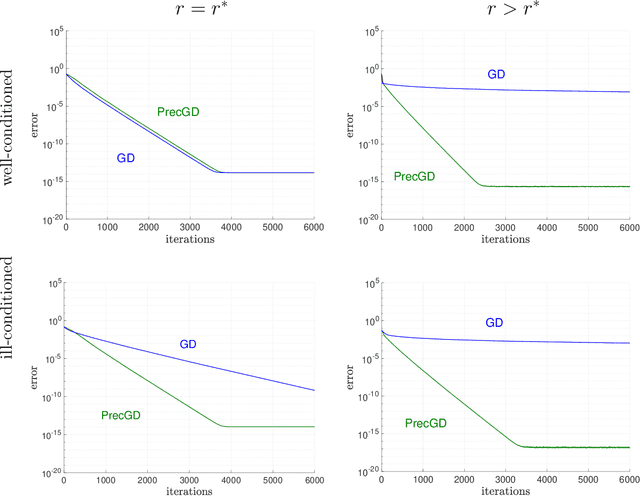
Preconditioned Gradient Descent for Over-Parameterized Nonconvex Matrix Factorization

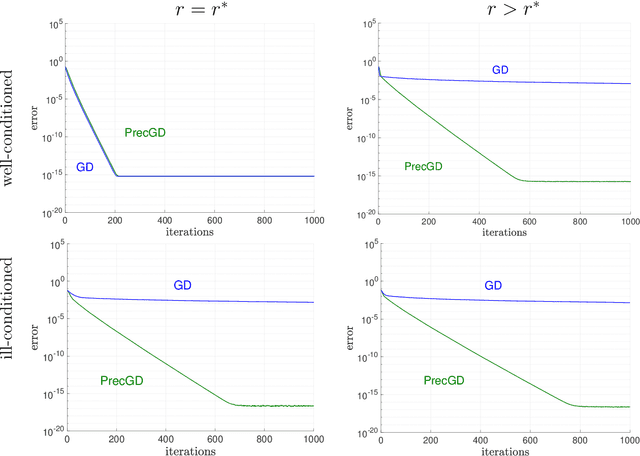
In practical instances of nonconvex matrix factorization, the rank of the true solution $r^{\star}$ is often unknown, so the rank $r$ of the model can be overspecified as $r>r^{\star}$. This over-parameterized regime of matrix factorization significantly slows down the convergence of local search algorithms, from a linear rate with $r=r^{\star}$ to a sublinear rate when $r>r^{\star}$. We propose an inexpensive preconditioner for the matrix sensing variant of nonconvex matrix factorization that restores the convergence rate of gradient descent back to linear, even in the over-parameterized case, while also making it agnostic to possible ill-conditioning in the ground truth. Classical gradient descent in a neighborhood of the solution slows down due to the need for the model matrix factor to become singular. Our key result is that this singularity can be corrected by $\ell_{2}$ regularization with a specific range of values for the damping parameter. In fact, a good damping parameter can be inexpensively estimated from the current iterate. The resulting algorithm, which we call preconditioned gradient descent or PrecGD, is stable under noise, and converges linearly to an information theoretically optimal error bound. Our numerical experiments find that PrecGD works equally well in restoring the linear convergence of other variants of nonconvex matrix factorization in the over-parameterized regime.

Statistically Optimal K-means Clustering via Nonnegative Low-rank Semidefinite Programming

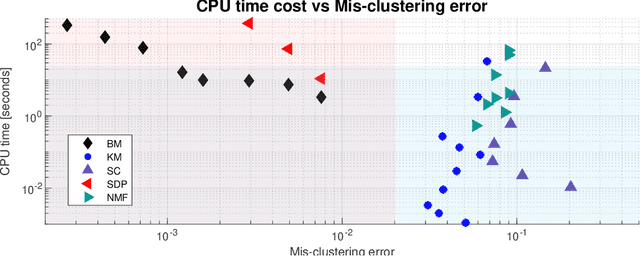
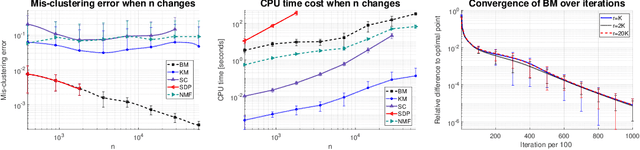
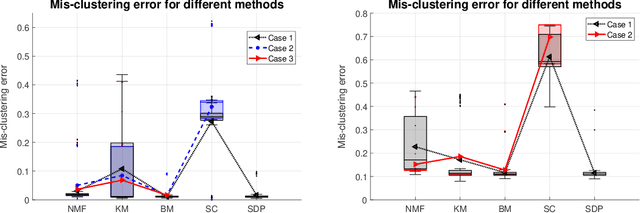
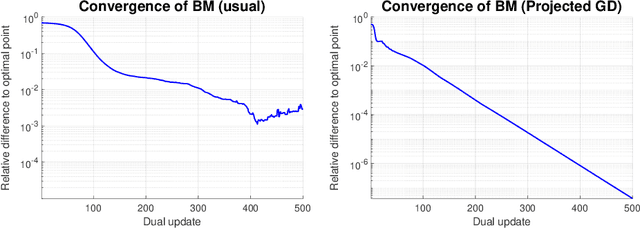
$K$-means clustering is a widely used machine learning method for identifying patterns in large datasets. Semidefinite programming (SDP) relaxations have recently been proposed for solving the $K$-means optimization problem that enjoy strong statistical optimality guarantees, but the prohibitive cost of implementing an SDP solver renders these guarantees inaccessible to practical datasets. By contrast, nonnegative matrix factorization (NMF) is a simple clustering algorithm that is widely used by machine learning practitioners, but without a solid statistical underpinning nor rigorous guarantees. In this paper, we describe an NMF-like algorithm that works by solving a nonnegative low-rank restriction of the SDP relaxed $K$-means formulation using a nonconvex Burer--Monteiro factorization approach. The resulting algorithm is just as simple and scalable as state-of-the-art NMF algorithms, while also enjoying the same strong statistical optimality guarantees as the SDP. In our experiments, we observe that our algorithm achieves substantially smaller mis-clustering errors compared to the existing state-of-the-art.

Fast and Minimax Optimal Estimation of Low-Rank Matrices via Non-Convex Gradient Descent

We study the problem of estimating a low-rank matrix from noisy measurements, with the specific goal of achieving minimax optimal error. In practice, the problem is commonly solved using non-convex gradient descent, due to its ability to scale to large-scale real-world datasets. In theory, non-convex gradient descent is capable of achieving minimax error. But in practice, it often converges extremely slowly, such that it cannot even deliver estimations of modest accuracy within reasonable time. On the other hand, methods that improve the convergence of non-convex gradient descent, through rescaling or preconditioning, also greatly amplify the measurement noise, resulting in estimations that are orders of magnitude less accurate than what is theoretically achievable with minimax optimal error. In this paper, we propose a slight modification to the usual non-convex gradient descent method that remedies the issue of slow convergence, while provably preserving its minimax optimality. Our proposed algorithm has essentially the same per-iteration cost as non-convex gradient descent, but is guaranteed to converge to minimax error at a linear rate that is immune to ill-conditioning. Using our proposed algorithm, we reconstruct a 60 megapixel dataset for a medical imaging application, and observe significantly decreased reconstruction error compared to previous approaches.

Overcoming the Convex Relaxation Barrier for Neural Network Verification via Nonconvex Low-Rank Semidefinite Relaxations

To rigorously certify the robustness of neural networks to adversarial perturbations, most state-of-the-art techniques rely on a triangle-shaped linear programming (LP) relaxation of the ReLU activation. While the LP relaxation is exact for a single neuron, recent results suggest that it faces an inherent "convex relaxation barrier" as additional activations are added, and as the attack budget is increased. In this paper, we propose a nonconvex relaxation for the ReLU relaxation, based on a low-rank restriction of a semidefinite programming (SDP) relaxation. We show that the nonconvex relaxation has a similar complexity to the LP relaxation, but enjoys improved tightness that is comparable to the much more expensive SDP relaxation. Despite nonconvexity, we prove that the verification problem satisfies constraint qualification, and therefore a Riemannian staircase approach is guaranteed to compute a near-globally optimal solution in polynomial time. Our experiments provide evidence that our nonconvex relaxation almost completely overcome the "convex relaxation barrier" faced by the LP relaxation.

Simple Alternating Minimization Provably Solves Complete Dictionary Learning

This paper focuses on complete dictionary learning problem, where the goal is to reparametrize a set of given signals as linear combinations of atoms from a learned dictionary. There are two main challenges faced by theoretical and practical studies of dictionary learning: the lack of theoretical guarantees for practically-used heuristic algorithms, and their poor scalability when dealing with huge-scale datasets. Towards addressing these issues, we show that when the dictionary to be learned is orthogonal, that an alternating minimization method directly applied to the nonconvex and discrete formulation of the problem exactly recovers the ground truth. For the huge-scale, potentially online setting, we propose a minibatch version of our algorithm, which can provably learn a complete dictionary from a huge-scale dataset with minimal sample complexity, linear sparsity level, and linear convergence rate, thereby negating the need for any convex relaxation for the problem. Our numerical experiments showcase the superiority of our method compared with the existing techniques when applied to tasks on real data.

Accelerating SGD for Highly Ill-Conditioned Huge-Scale Online Matrix Completion

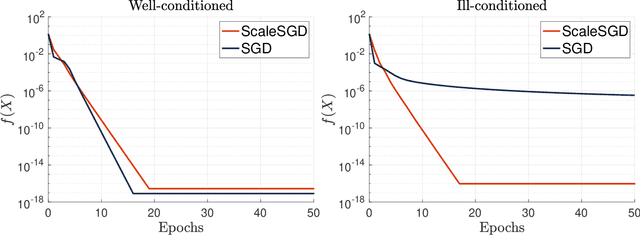
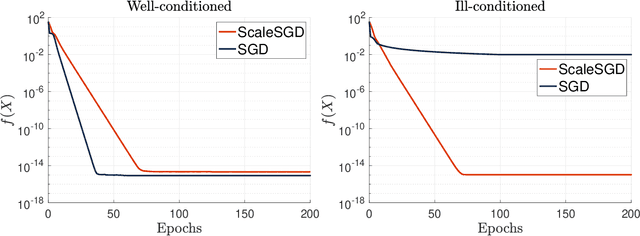
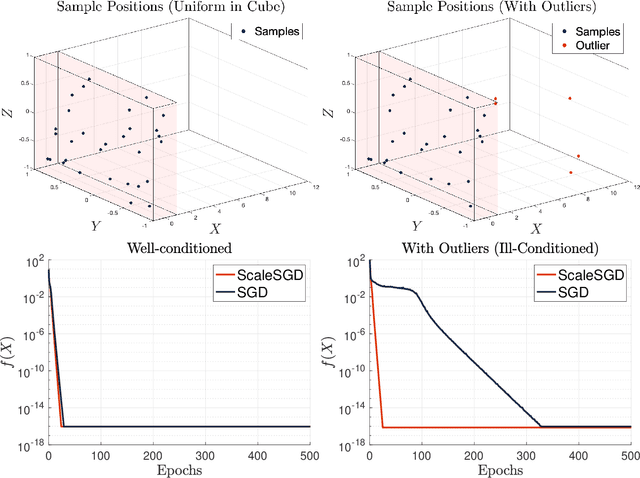
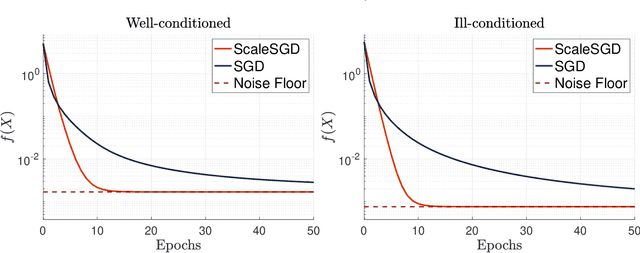
The matrix completion problem seeks to recover a $d\times d$ ground truth matrix of low rank $r\ll d$ from observations of its individual elements. Real-world matrix completion is often a huge-scale optimization problem, with $d$ so large that even the simplest full-dimension vector operations with $O(d)$ time complexity become prohibitively expensive. Stochastic gradient descent (SGD) is one of the few algorithms capable of solving matrix completion on a huge scale, and can also naturally handle streaming data over an evolving ground truth. Unfortunately, SGD experiences a dramatic slow-down when the underlying ground truth is ill-conditioned; it requires at least $O(\kappa\log(1/\epsilon))$ iterations to get $\epsilon$-close to ground truth matrix with condition number $\kappa$. In this paper, we propose a preconditioned version of SGD that preserves all the favorable practical qualities of SGD for huge-scale online optimization while also making it agnostic to $\kappa$. For a symmetric ground truth and the Root Mean Square Error (RMSE) loss, we prove that the preconditioned SGD converges to $\epsilon$-accuracy in $O(\log(1/\epsilon))$ iterations, with a rapid linear convergence rate as if the ground truth were perfectly conditioned with $\kappa=1$. In our numerical experiments, we observe a similar acceleration for ill-conditioned matrix completion under the 1-bit cross-entropy loss, as well as pairwise losses such as the Bayesian Personalized Ranking (BPR) loss.

Improved Global Guarantees for the Nonconvex Burer--Monteiro Factorization via Rank Overparameterization

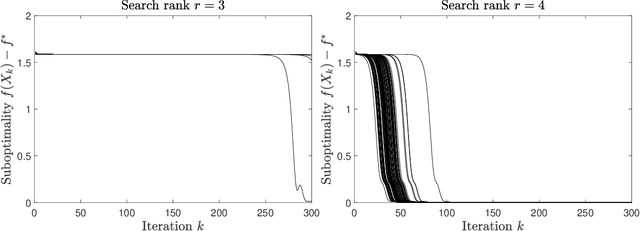
We consider minimizing a twice-differentiable, $L$-smooth, and $\mu$-strongly convex objective $\phi$ over an $n\times n$ positive semidefinite matrix $M\succeq0$, under the assumption that the minimizer $M^{\star}$ has low rank $r^{\star}\ll n$. Following the Burer--Monteiro approach, we instead minimize the nonconvex objective $f(X)=\phi(XX^{T})$ over a factor matrix $X$ of size $n\times r$. This substantially reduces the number of variables from $O(n^{2})$ to as few as $O(n)$ and also enforces positive semidefiniteness for free, but at the cost of giving up the convexity of the original problem. In this paper, we prove that if the search rank $r\ge r^{\star}$ is overparameterized by a constant factor with respect to the true rank $r^{\star}$, namely as in $r>\frac{1}{4}(L/\mu-1)^{2}r^{\star}$, then despite nonconvexity, local optimization is guaranteed to globally converge from any initial point to the global optimum. This significantly improves upon a previous rank overparameterization threshold of $r\ge n$, which is known to be sharp if $\phi$ is allowed to be nonsmooth and/or non-strongly convex, but would increase the number of variables back up to $O(n^{2})$. Conversely, without rank overparameterization, we prove that such a global guarantee is possible if and only if $\phi$ is almost perfectly conditioned, with a condition number of $L/\mu<3$. Therefore, we conclude that a small amount of overparameterization can lead to large improvements in theoretical guarantees for the nonconvex Burer--Monteiro factorization.

Preconditioned Gradient Descent for Overparameterized Nonconvex Burer--Monteiro Factorization with Global Optimality Certification

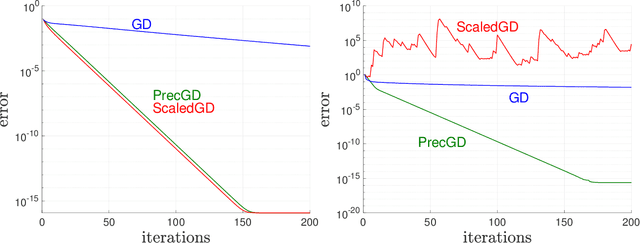
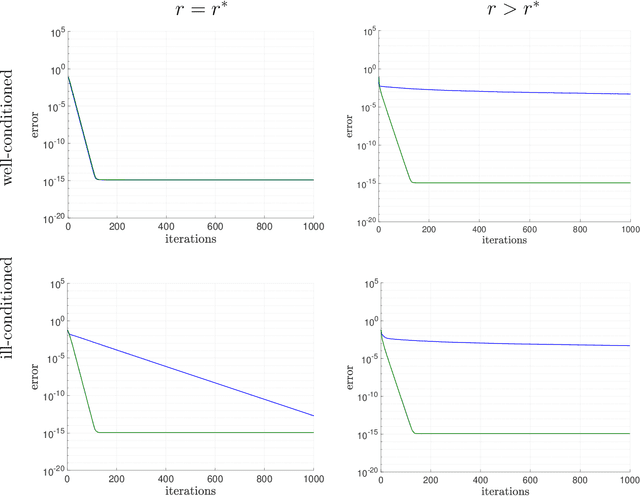
We consider using gradient descent to minimize the nonconvex function $f(X)=\phi(XX^{T})$ over an $n\times r$ factor matrix $X$, in which $\phi$ is an underlying smooth convex cost function defined over $n\times n$ matrices. While only a second-order stationary point $X$ can be provably found in reasonable time, if $X$ is additionally rank deficient, then its rank deficiency certifies it as being globally optimal. This way of certifying global optimality necessarily requires the search rank $r$ of the current iterate $X$ to be overparameterized with respect to the rank $r^{\star}$ of the global minimizer $X^{\star}$. Unfortunately, overparameterization significantly slows down the convergence of gradient descent, from a linear rate with $r=r^{\star}$ to a sublinear rate when $r>r^{\star}$, even when $\phi$ is strongly convex. In this paper, we propose an inexpensive preconditioner that restores the convergence rate of gradient descent back to linear in the overparameterized case, while also making it agnostic to possible ill-conditioning in the global minimizer $X^{\star}$.