Improved Global Guarantees for the Nonconvex Burer--Monteiro Factorization via Rank Overparameterization
Paper and Code
Jul 05, 2022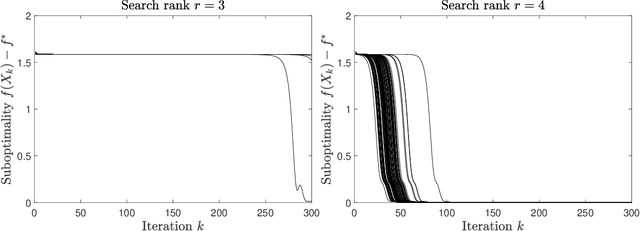
We consider minimizing a twice-differentiable, $L$-smooth, and $\mu$-strongly convex objective $\phi$ over an $n\times n$ positive semidefinite matrix $M\succeq0$, under the assumption that the minimizer $M^{\star}$ has low rank $r^{\star}\ll n$. Following the Burer--Monteiro approach, we instead minimize the nonconvex objective $f(X)=\phi(XX^{T})$ over a factor matrix $X$ of size $n\times r$. This substantially reduces the number of variables from $O(n^{2})$ to as few as $O(n)$ and also enforces positive semidefiniteness for free, but at the cost of giving up the convexity of the original problem. In this paper, we prove that if the search rank $r\ge r^{\star}$ is overparameterized by a constant factor with respect to the true rank $r^{\star}$, namely as in $r>\frac{1}{4}(L/\mu-1)^{2}r^{\star}$, then despite nonconvexity, local optimization is guaranteed to globally converge from any initial point to the global optimum. This significantly improves upon a previous rank overparameterization threshold of $r\ge n$, which is known to be sharp if $\phi$ is allowed to be nonsmooth and/or non-strongly convex, but would increase the number of variables back up to $O(n^{2})$. Conversely, without rank overparameterization, we prove that such a global guarantee is possible if and only if $\phi$ is almost perfectly conditioned, with a condition number of $L/\mu<3$. Therefore, we conclude that a small amount of overparameterization can lead to large improvements in theoretical guarantees for the nonconvex Burer--Monteiro factorization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge