Statistically Optimal K-means Clustering via Nonnegative Low-rank Semidefinite Programming

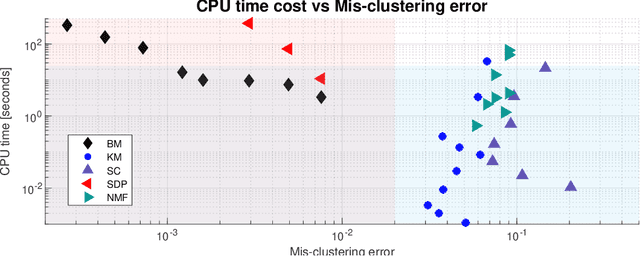
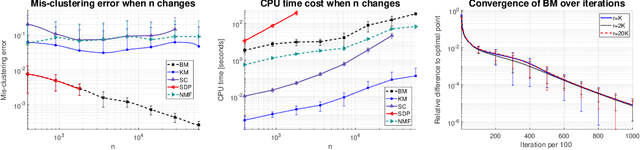
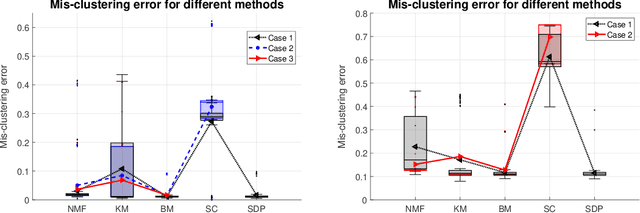
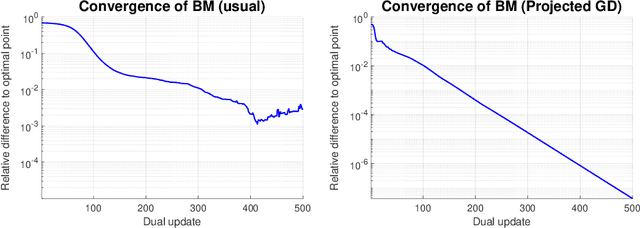
$K$-means clustering is a widely used machine learning method for identifying patterns in large datasets. Semidefinite programming (SDP) relaxations have recently been proposed for solving the $K$-means optimization problem that enjoy strong statistical optimality guarantees, but the prohibitive cost of implementing an SDP solver renders these guarantees inaccessible to practical datasets. By contrast, nonnegative matrix factorization (NMF) is a simple clustering algorithm that is widely used by machine learning practitioners, but without a solid statistical underpinning nor rigorous guarantees. In this paper, we describe an NMF-like algorithm that works by solving a nonnegative low-rank restriction of the SDP relaxed $K$-means formulation using a nonconvex Burer--Monteiro factorization approach. The resulting algorithm is just as simple and scalable as state-of-the-art NMF algorithms, while also enjoying the same strong statistical optimality guarantees as the SDP. In our experiments, we observe that our algorithm achieves substantially smaller mis-clustering errors compared to the existing state-of-the-art.

Likelihood adjusted semidefinite programs for clustering heterogeneous data

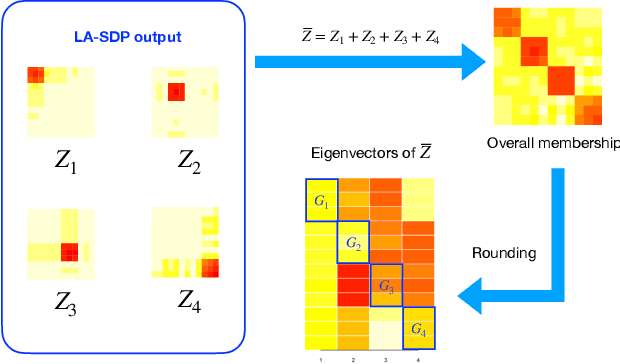
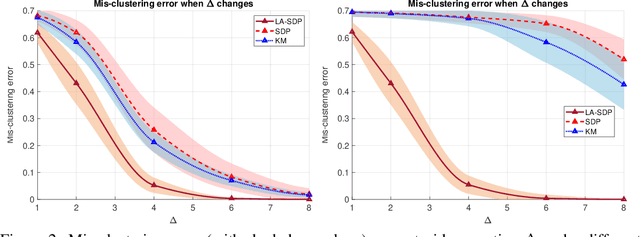
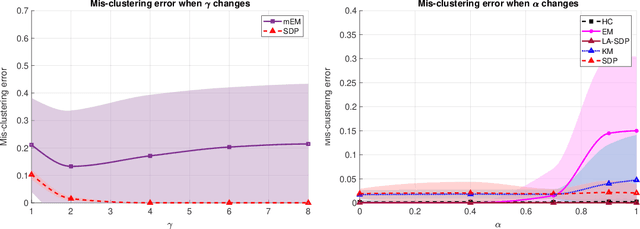
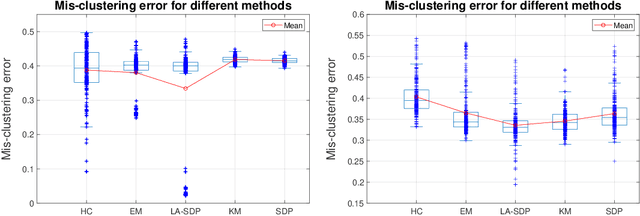
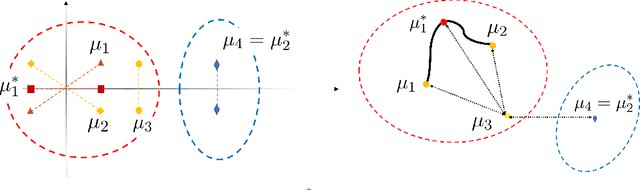
Clustering is a widely deployed unsupervised learning tool. Model-based clustering is a flexible framework to tackle data heterogeneity when the clusters have different shapes. Likelihood-based inference for mixture distributions often involves non-convex and high-dimensional objective functions, imposing difficult computational and statistical challenges. The classic expectation-maximization (EM) algorithm is a computationally thrifty iterative method that maximizes a surrogate function minorizing the log-likelihood of observed data in each iteration, which however suffers from bad local maxima even in the special case of the standard Gaussian mixture model with common isotropic covariance matrices. On the other hand, recent studies reveal that the unique global solution of a semidefinite programming (SDP) relaxed $K$-means achieves the information-theoretically sharp threshold for perfectly recovering the cluster labels under the standard Gaussian mixture model. In this paper, we extend the SDP approach to a general setting by integrating cluster labels as model parameters and propose an iterative likelihood adjusted SDP (iLA-SDP) method that directly maximizes the \emph{exact} observed likelihood in the presence of data heterogeneity. By lifting the cluster assignment to group-specific membership matrices, iLA-SDP avoids centroids estimation -- a key feature that allows exact recovery under well-separateness of centroids without being trapped by their adversarial configurations. Thus iLA-SDP is less sensitive than EM to initialization and more stable on high-dimensional data. Our numeric experiments demonstrate that iLA-SDP can achieve lower mis-clustering errors over several widely used clustering methods including $K$-means, SDP and EM algorithms.

Wasserstein $K$-means for clustering probability distributions

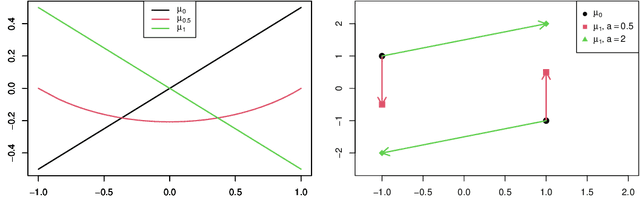
Clustering is an important exploratory data analysis technique to group objects based on their similarity. The widely used $K$-means clustering method relies on some notion of distance to partition data into a fewer number of groups. In the Euclidean space, centroid-based and distance-based formulations of the $K$-means are equivalent. In modern machine learning applications, data often arise as probability distributions and a natural generalization to handle measure-valued data is to use the optimal transport metric. Due to non-negative Alexandrov curvature of the Wasserstein space, barycenters suffer from regularity and non-robustness issues. The peculiar behaviors of Wasserstein barycenters may make the centroid-based formulation fail to represent the within-cluster data points, while the more direct distance-based $K$-means approach and its semidefinite program (SDP) relaxation are capable of recovering the true cluster labels. In the special case of clustering Gaussian distributions, we show that the SDP relaxed Wasserstein $K$-means can achieve exact recovery given the clusters are well-separated under the $2$-Wasserstein metric. Our simulation and real data examples also demonstrate that distance-based $K$-means can achieve better classification performance over the standard centroid-based $K$-means for clustering probability distributions and images.

Sketch-and-Lift: Scalable Subsampled Semidefinite Program for $K$-means Clustering

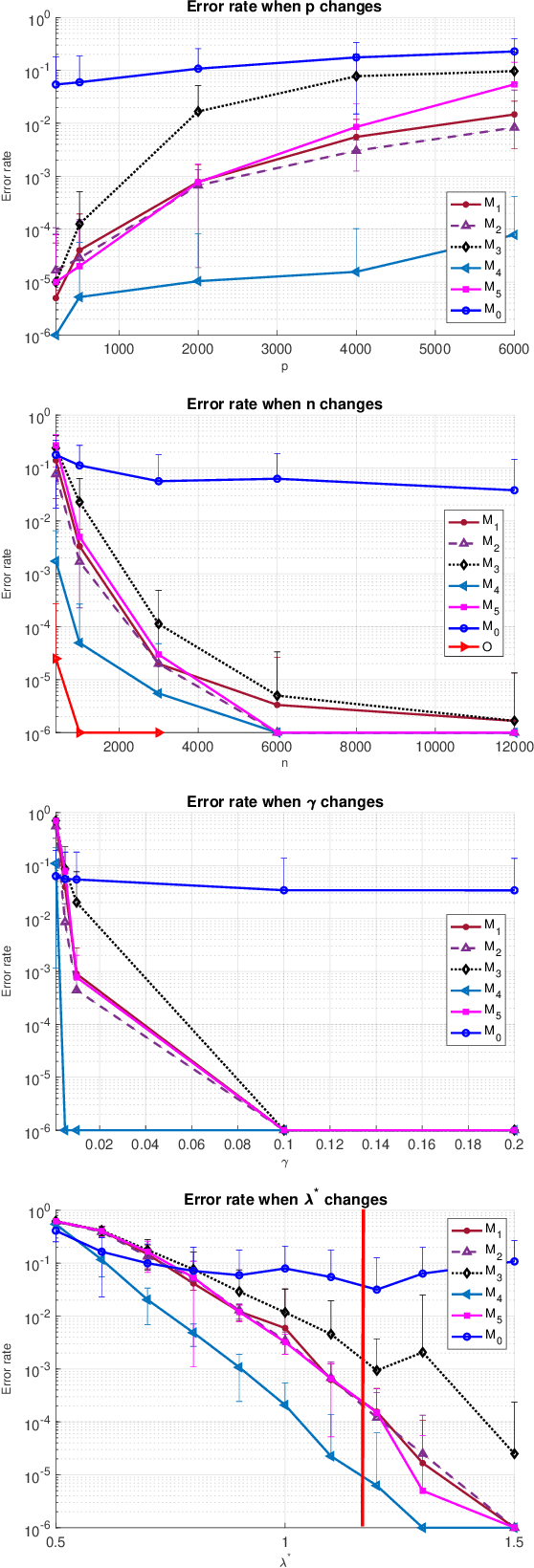
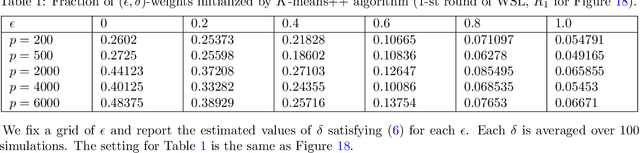
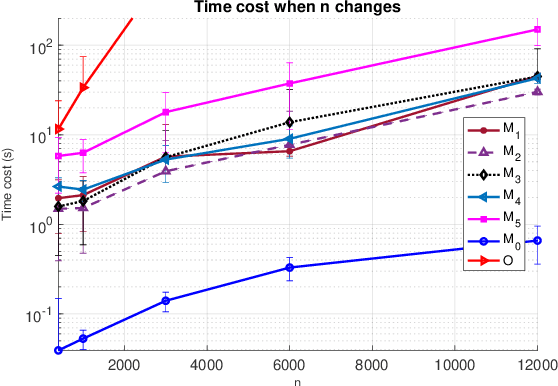
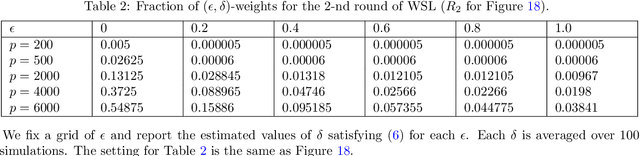
Semidefinite programming (SDP) is a powerful tool for tackling a wide range of computationally hard problems such as clustering. Despite the high accuracy, semidefinite programs are often too slow in practice with poor scalability on large (or even moderate) datasets. In this paper, we introduce a linear time complexity algorithm for approximating an SDP relaxed $K$-means clustering. The proposed sketch-and-lift (SL) approach solves an SDP on a subsampled dataset and then propagates the solution to all data points by a nearest-centroid rounding procedure. It is shown that the SL approach enjoys a similar exact recovery threshold as the $K$-means SDP on the full dataset, which is known to be information-theoretically tight under the Gaussian mixture model. The SL method can be made adaptive with enhanced theoretic properties when the cluster sizes are unbalanced. Our simulation experiments demonstrate that the statistical accuracy of the proposed method outperforms state-of-the-art fast clustering algorithms without sacrificing too much computational efficiency, and is comparable to the original $K$-means SDP with substantially reduced runtime.