Wasserstein $K$-means for clustering probability distributions
Paper and Code
Sep 14, 2022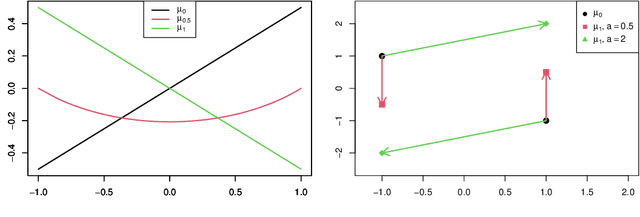

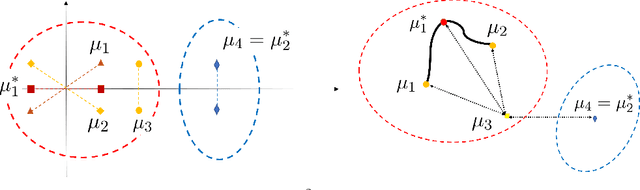

Clustering is an important exploratory data analysis technique to group objects based on their similarity. The widely used $K$-means clustering method relies on some notion of distance to partition data into a fewer number of groups. In the Euclidean space, centroid-based and distance-based formulations of the $K$-means are equivalent. In modern machine learning applications, data often arise as probability distributions and a natural generalization to handle measure-valued data is to use the optimal transport metric. Due to non-negative Alexandrov curvature of the Wasserstein space, barycenters suffer from regularity and non-robustness issues. The peculiar behaviors of Wasserstein barycenters may make the centroid-based formulation fail to represent the within-cluster data points, while the more direct distance-based $K$-means approach and its semidefinite program (SDP) relaxation are capable of recovering the true cluster labels. In the special case of clustering Gaussian distributions, we show that the SDP relaxed Wasserstein $K$-means can achieve exact recovery given the clusters are well-separated under the $2$-Wasserstein metric. Our simulation and real data examples also demonstrate that distance-based $K$-means can achieve better classification performance over the standard centroid-based $K$-means for clustering probability distributions and images.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge