Towards Understanding the Power and Limits of the Muon Optimizer: A River-Valley Perspective

Recently, Muon has gained substantial attention as an appealing alternative to Adam-like optimizers, with many works highlighting its advantages through spectral normalization and improved conditioning. Yet this positive theoretical narrative contrasts with its empirical performance in large language model (LLM) training, where Muon's gains over Adam/AdamW are often mixed, schedule-sensitive, and not uniformly superior. To address this gap, we develop a trajectory-level theory characterizing both the strengths and limitations of Muon. We introduce a mixed-spiked matrix sensing model whose sensing operator decomposes into signal, spike, and bulk components, capturing a mixture of anisotropic structure and long-tail information reminiscent of LLM training. On top of it, we adopted a river-valley perspective in which we view the landscape as composed of a river direction flowing to the desired solution and hill directions encoding nuisance or task-irrelevant information. In the momentum-free setting, we show that Muon moves faster along the information-bearing river direction during early optimization, but can converge much more slowly near the river bottom than gradient descent. We then extend the river-valley perspective to general nonconvex objectives with momentum by studying points on the spectral river. There, while Muon converges faster early on, its orthogonalized update removes residual scale information, making it prone to overshooting and oscillation near the target solution. Together, these results suggest that our characterizations extend beyond spiked matrix sensing and motivate switching to GD-like refinement optimizers in the final phase, rather than relying only on a fixed learning-rate schedule for Muon. We also provide preliminary evidence supporting this two-stage approach in language model training experiments.

Understanding Quantization-Aware Training: Gradients at Quantized Weights Bias to the Low-Loss Basin

Post-training quantization (PTQ) converts a trained full-precision model into low-bit weights without task-level retraining, while quantization-aware training (QAT) incorporates quantization into the training loop. Although PTQ is efficient and often accurate at moderate bitwidths, it can fail sharply at aggressive bitwidths; QAT is more expensive but can often recover the lost accuracy. We propose a unified geometric framework that explains both PTQ failure and QAT recovery. We model full-precision training as following a low-loss \emph{river} inside a wider \emph{valley}: a normal neighborhood of the river forms a nearly flat \emph{basin}, while leaving this basin incurs a sharp loss increase. When the quantization grid is comparable to the basin width, local PTQ objectives, including rounding and Hessian-based second-order reconstruction, can select a high-loss deployed quantized point outside the basin even when nearby low-loss quantized points exist. In this regime, straight-through-estimator-based QAT has a useful bias: it evaluates gradients at the deployed quantized weights while updating latent full-precision weights, causing the gradient to sense the valley wall and acquire an inward component that steers subsequent quantized iterates back into the basin. We formalize this mechanism through a local landscape model, construct a geometric PTQ failure mode, and prove finite-time QAT recovery under local quantizer-compatibility assumptions. Experiments across vision and language models under multiple neural-network quantization schemes corroborate the predicted basin-crossing failure of PTQ and the corresponding recovery mechanism of QAT.

Preconditioning Benefits of Spectral Orthogonalization in Muon

The Muon optimizer, a matrix-structured algorithm that leverages spectral orthogonalization of gradients, is a milestone in the pretraining of large language models. However, the underlying mechanisms of Muon -- particularly the role of gradient orthogonalization -- remain poorly understood, with very few works providing end-to-end analyses that rigorously explain its advantages in concrete applications. We take a step by studying the effectiveness of a simplified variant of Muon through two case studies: matrix factorization, and in-context learning of linear transformers. For both problems, we prove that simplified Muon converges linearly with iteration complexities independent of the relevant condition number, provably outperforming gradient descent and Adam. Our analysis reveals that the Muon dynamics decouple into a collection of independent scalar sequences in the spectral domain, each exhibiting similar convergence behavior. Our theory formalizes the preconditioning effect induced by spectral orthogonalization, offering insight into Muon's effectiveness in these matrix optimization problems and potentially beyond.

LIBRA: Language Model Informed Bandit Recourse Algorithm for Personalized Treatment Planning

We introduce a unified framework that seamlessly integrates algorithmic recourse, contextual bandits, and large language models (LLMs) to support sequential decision-making in high-stakes settings such as personalized medicine. We first introduce the recourse bandit problem, where a decision-maker must select both a treatment action and a feasible, minimal modification to mutable patient features. To address this problem, we develop the Generalized Linear Recourse Bandit (GLRB) algorithm. Building on this foundation, we propose LIBRA, a Language Model-Informed Bandit Recourse Algorithm that strategically combines domain knowledge from LLMs with the statistical rigor of bandit learning. LIBRA offers three key guarantees: (i) a warm-start guarantee, showing that LIBRA significantly reduces initial regret when LLM recommendations are near-optimal; (ii) an LLM-effort guarantee, proving that the algorithm consults the LLM only $O(\log^2 T)$ times, where $T$ is the time horizon, ensuring long-term autonomy; and (iii) a robustness guarantee, showing that LIBRA never performs worse than a pure bandit algorithm even when the LLM is unreliable. We further establish matching lower bounds that characterize the fundamental difficulty of the recourse bandit problem and demonstrate the near-optimality of our algorithms. Experiments on synthetic environments and a real hypertension-management case study confirm that GLRB and LIBRA improve regret, treatment quality, and sample efficiency compared with standard contextual bandits and LLM-only benchmarks. Our results highlight the promise of recourse-aware, LLM-assisted bandit algorithms for trustworthy LLM-bandits collaboration in personalized high-stakes decision-making.

Implicit Regularization of Infinitesimally-perturbed Gradient Descent Toward Low-dimensional Solutions

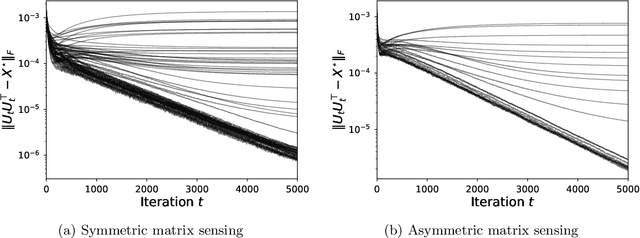
Implicit regularization refers to the phenomenon where local search algorithms converge to low-dimensional solutions, even when such structures are neither explicitly specified nor encoded in the optimization problem. While widely observed, this phenomenon remains theoretically underexplored, particularly in modern over-parameterized problems. In this paper, we study the conditions that enable implicit regularization by investigating when gradient-based methods converge to second-order stationary points (SOSPs) within an implicit low-dimensional region of a smooth, possibly nonconvex function. We show that successful implicit regularization hinges on two key conditions: $(i)$ the ability to efficiently escape strict saddle points, while $(ii)$ maintaining proximity to the implicit region. Existing analyses enabling the convergence of gradient descent (GD) to SOSPs often rely on injecting large perturbations to escape strict saddle points. However, this comes at the cost of deviating from the implicit region. The central premise of this paper is that it is possible to achieve the best of both worlds: efficiently escaping strict saddle points using infinitesimal perturbations, while controlling deviation from the implicit region via a small deviation rate. We show that infinitesimally perturbed gradient descent (IPGD), which can be interpreted as GD with inherent ``round-off errors'', can provably satisfy both conditions. We apply our framework to the problem of over-parameterized matrix sensing, where we establish formal guarantees for the implicit regularization behavior of IPGD. We further demonstrate through extensive experiments that these insights extend to a broader class of learning problems.

RANSAC Revisited: An Improved Algorithm for Robust Subspace Recovery under Adversarial and Noisy Corruptions

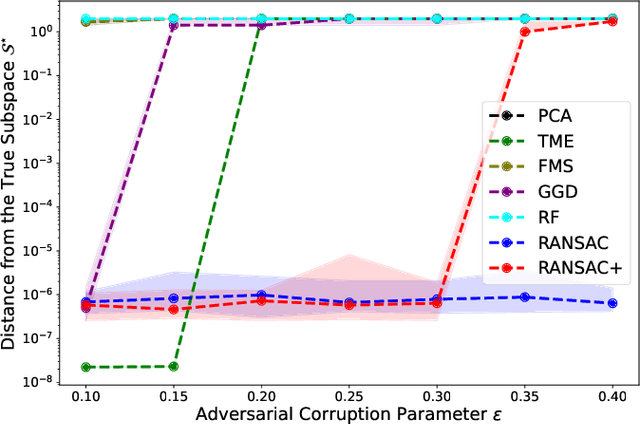
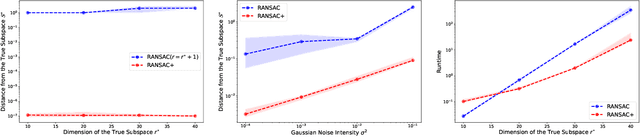
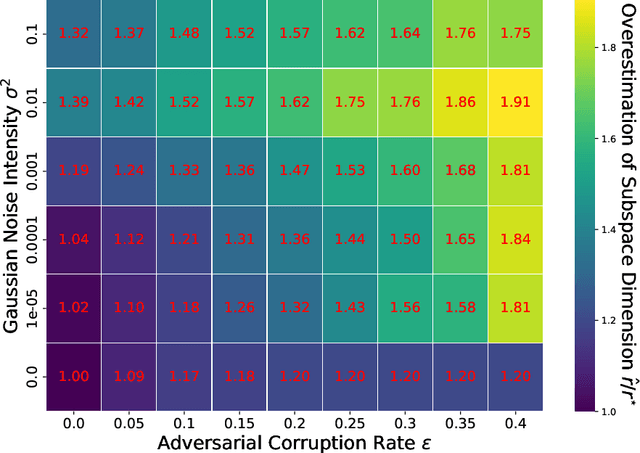
In this paper, we study the problem of robust subspace recovery (RSR) in the presence of both strong adversarial corruptions and Gaussian noise. Specifically, given a limited number of noisy samples -- some of which are tampered by an adaptive and strong adversary -- we aim to recover a low-dimensional subspace that approximately contains a significant fraction of the uncorrupted samples, up to an error that scales with the Gaussian noise. Existing approaches to this problem often suffer from high computational costs or rely on restrictive distributional assumptions, limiting their applicability in truly adversarial settings. To address these challenges, we revisit the classical random sample consensus (RANSAC) algorithm, which offers strong robustness to adversarial outliers, but sacrifices efficiency and robustness against Gaussian noise and model misspecification in the process. We propose a two-stage algorithm, RANSAC+, that precisely pinpoints and remedies the failure modes of standard RANSAC. Our method is provably robust to both Gaussian and adversarial corruptions, achieves near-optimal sample complexity without requiring prior knowledge of the subspace dimension, and is more efficient than existing RANSAC-type methods.

PARQ: Piecewise-Affine Regularized Quantization

We develop a principled method for quantization-aware training (QAT) of large-scale machine learning models. Specifically, we show that convex, piecewise-affine regularization (PAR) can effectively induce the model parameters to cluster towards discrete values. We minimize PAR-regularized loss functions using an aggregate proximal stochastic gradient method (AProx) and prove that it has last-iterate convergence. Our approach provides an interpretation of the straight-through estimator (STE), a widely used heuristic for QAT, as the asymptotic form of PARQ. We conduct experiments to demonstrate that PARQ obtains competitive performance on convolution- and transformer-based vision tasks.

Convergence of Gradient Descent with Small Initialization for Unregularized Matrix Completion

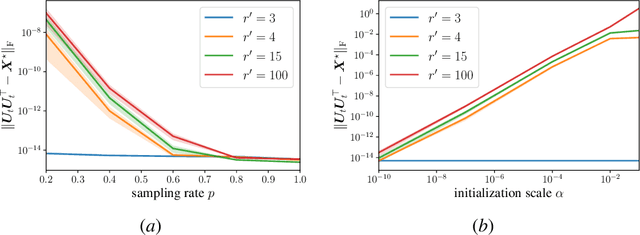
We study the problem of symmetric matrix completion, where the goal is to reconstruct a positive semidefinite matrix $\rm{X}^\star \in \mathbb{R}^{d\times d}$ of rank-$r$, parameterized by $\rm{U}\rm{U}^{\top}$, from only a subset of its observed entries. We show that the vanilla gradient descent (GD) with small initialization provably converges to the ground truth $\rm{X}^\star$ without requiring any explicit regularization. This convergence result holds true even in the over-parameterized scenario, where the true rank $r$ is unknown and conservatively over-estimated by a search rank $r'\gg r$. The existing results for this problem either require explicit regularization, a sufficiently accurate initial point, or exact knowledge of the true rank $r$. In the over-parameterized regime where $r'\geq r$, we show that, with $\widetilde\Omega(dr^9)$ observations, GD with an initial point $\|\rm{U}_0\| \leq \epsilon$ converges near-linearly to an $\epsilon$-neighborhood of $\rm{X}^\star$. Consequently, smaller initial points result in increasingly accurate solutions. Surprisingly, neither the convergence rate nor the final accuracy depends on the over-parameterized search rank $r'$, and they are only governed by the true rank $r$. In the exactly-parameterized regime where $r'=r$, we further enhance this result by proving that GD converges at a faster rate to achieve an arbitrarily small accuracy $\epsilon>0$, provided the initial point satisfies $\|\rm{U}_0\| = O(1/d)$. At the crux of our method lies a novel weakly-coupled leave-one-out analysis, which allows us to establish the global convergence of GD, extending beyond what was previously possible using the classical leave-one-out analysis.

Robust Sparse Mean Estimation via Incremental Learning

In this paper, we study the problem of robust sparse mean estimation, where the goal is to estimate a $k$-sparse mean from a collection of partially corrupted samples drawn from a heavy-tailed distribution. Existing estimators face two critical challenges in this setting. First, they are limited by a conjectured computational-statistical tradeoff, implying that any computationally efficient algorithm needs $\tilde\Omega(k^2)$ samples, while its statistically-optimal counterpart only requires $\tilde O(k)$ samples. Second, the existing estimators fall short of practical use as they scale poorly with the ambient dimension. This paper presents a simple mean estimator that overcomes both challenges under moderate conditions: it runs in near-linear time and memory (both with respect to the ambient dimension) while requiring only $\tilde O(k)$ samples to recover the true mean. At the core of our method lies an incremental learning phenomenon: we introduce a simple nonconvex framework that can incrementally learn the top-$k$ nonzero elements of the mean while keeping the zero elements arbitrarily small. Unlike existing estimators, our method does not need any prior knowledge of the sparsity level $k$. We prove the optimality of our estimator by providing a matching information-theoretic lower bound. Finally, we conduct a series of simulations to corroborate our theoretical findings. Our code is available at https://github.com/huihui0902/Robust_mean_estimation.

On the Optimization Landscape of Burer-Monteiro Factorization: When do Global Solutions Correspond to Ground Truth?

In low-rank matrix recovery, the goal is to recover a low-rank matrix, given a limited number of linear and possibly noisy measurements. Low-rank matrix recovery is typically solved via a nonconvex method called Burer-Monteiro factorization (BM). If the rank of the ground truth is known, BM is free of sub-optimal local solutions, and its true solutions coincide with the global solutions -- that is, the true solutions are identifiable. When the rank of the ground truth is unknown, it must be over-estimated, giving rise to an over-parameterized BM. In the noiseless regime, it is recently shown that over-estimation of the rank leads to progressively fewer sub-optimal local solutions while preserving the identifiability of the true solutions. In this work, we show that with noisy measurements, the global solutions of the over-parameterized BM no longer correspond to the true solutions, essentially transmuting over-parameterization from blessing to curse. In particular, we study two classes of low-rank matrix recovery, namely matrix completion and matrix sensing. For matrix completion, we show that even if the rank is only slightly over-estimated and with very mild assumptions on the noise, none of the true solutions are local or global solutions. For matrix sensing, we show that to guarantee the correspondence between global and true solutions, it is necessary and sufficient for the number of samples to scale linearly with the over-estimated rank, which can be drastically larger than its optimal sample complexity that only scales with the true rank.