Jiaye Teng
Smoothing-Based Conformal Prediction for Balancing Efficiency and Interpretability
Sep 26, 2025Abstract:Conformal Prediction (CP) is a distribution-free framework for constructing statistically rigorous prediction sets. While popular variants such as CD-split improve CP's efficiency, they often yield prediction sets composed of multiple disconnected subintervals, which are difficult to interpret. In this paper, we propose SCD-split, which incorporates smoothing operations into the CP framework. Such smoothing operations potentially help merge the subintervals, thus leading to interpretable prediction sets. Experimental results on both synthetic and real-world datasets demonstrate that SCD-split balances the interval length and the number of disconnected subintervals. Theoretically, under specific conditions, SCD-split provably reduces the number of disconnected subintervals while maintaining comparable coverage guarantees and interval length compared with CD-split.
Disentangling Feature Structure: A Mathematically Provable Two-Stage Training Dynamics in Transformers
Feb 28, 2025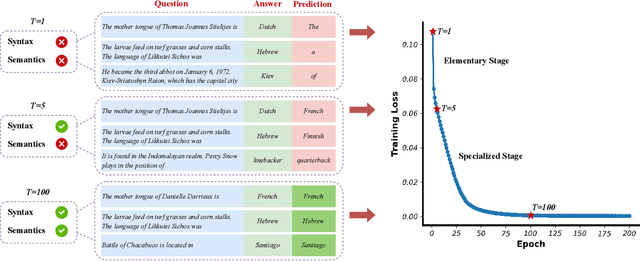

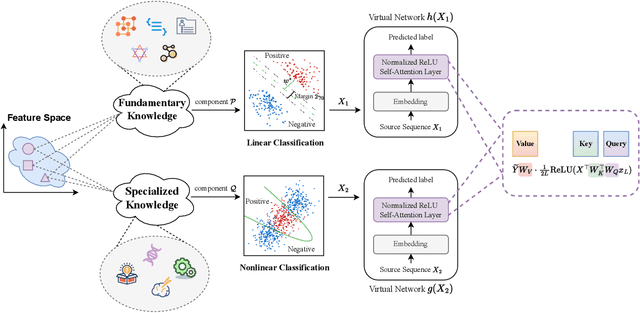
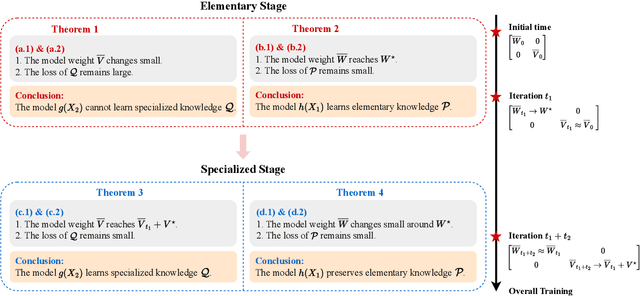
Abstract:Transformers may exhibit two-stage training dynamics during the real-world training process. For instance, when training GPT-2 on the Counterfact dataset, the answers progress from syntactically incorrect to syntactically correct to semantically correct. However, existing theoretical analyses hardly account for this two-stage phenomenon. In this paper, we theoretically demonstrate how such two-stage training dynamics occur in transformers. Specifically, we analyze the dynamics of transformers using feature learning techniques under in-context learning regimes, based on a disentangled two-type feature structure. Such disentanglement of feature structure is general in practice, e.g., natural languages contain syntax and semantics, and proteins contain primary and secondary structures. To our best known, this is the first rigorous result regarding a two-stage optimization process in transformers. Additionally, a corollary indicates that such a two-stage process is closely related to the spectral properties of the attention weights, which accords well with empirical findings.
Predictive Inference With Fast Feature Conformal Prediction
Dec 01, 2024Abstract:Conformal prediction is widely adopted in uncertainty quantification, due to its post-hoc, distribution-free, and model-agnostic properties. In the realm of modern deep learning, researchers have proposed Feature Conformal Prediction (FCP), which deploys conformal prediction in a feature space, yielding reduced band lengths. However, the practical utility of FCP is limited due to the time-consuming non-linear operations required to transform confidence bands from feature space to output space. In this paper, we introduce Fast Feature Conformal Prediction (FFCP), which features a novel non-conformity score and is convenient for practical applications. FFCP serves as a fast version of FCP, in that it equivalently employs a Taylor expansion to approximate the aforementioned non-linear operations in FCP. Empirical validations showcase that FFCP performs comparably with FCP (both outperforming the vanilla version) while achieving a significant reduction in computational time by approximately 50x. The code is available at https://github.com/ElvisWang1111/FastFeatureCP
On Uni-Modal Feature Learning in Supervised Multi-Modal Learning
May 03, 2023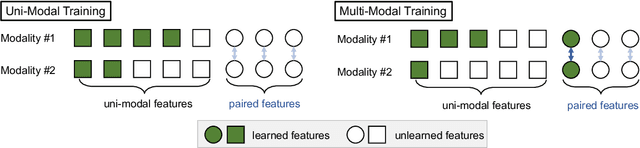
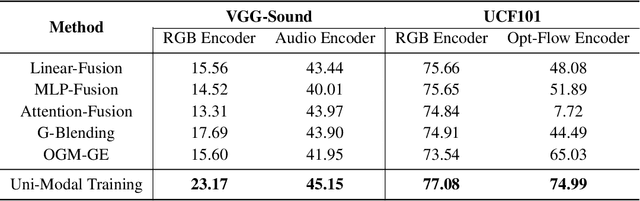
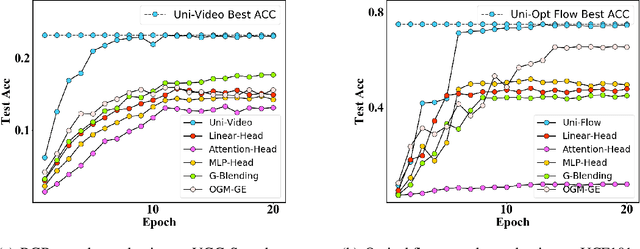
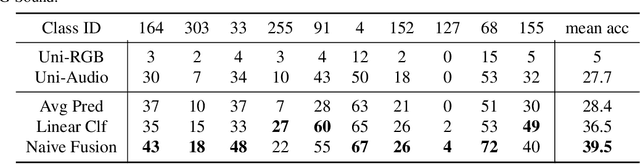
Abstract:We abstract the features (i.e. learned representations) of multi-modal data into 1) uni-modal features, which can be learned from uni-modal training, and 2) paired features, which can only be learned from cross-modal interactions. Multi-modal models are expected to benefit from cross-modal interactions on the basis of ensuring uni-modal feature learning. However, recent supervised multi-modal late-fusion training approaches still suffer from insufficient learning of uni-modal features on each modality. We prove that this phenomenon does hurt the model's generalization ability. To this end, we propose to choose a targeted late-fusion learning method for the given supervised multi-modal task from Uni-Modal Ensemble(UME) and the proposed Uni-Modal Teacher(UMT), according to the distribution of uni-modal and paired features. We demonstrate that, under a simple guiding strategy, we can achieve comparable results to other complex late-fusion or intermediate-fusion methods on various multi-modal datasets, including VGG-Sound, Kinetics-400, UCF101, and ModelNet40.
Lower Generalization Bounds for GD and SGD in Smooth Stochastic Convex Optimization
Mar 19, 2023Abstract:Recent progress was made in characterizing the generalization error of gradient methods for general convex loss by the learning theory community. In this work, we focus on how training longer might affect generalization in smooth stochastic convex optimization (SCO) problems. We first provide tight lower bounds for general non-realizable SCO problems. Furthermore, existing upper bound results suggest that sample complexity can be improved by assuming the loss is realizable, i.e. an optimal solution simultaneously minimizes all the data points. However, this improvement is compromised when training time is long and lower bounds are lacking. Our paper examines this observation by providing excess risk lower bounds for gradient descent (GD) and stochastic gradient descent (SGD) in two realizable settings: 1) realizable with $T = O(n)$, and (2) realizable with $T = \Omega(n)$, where $T$ denotes the number of training iterations and $n$ is the size of the training dataset. These bounds are novel and informative in characterizing the relationship between $T$ and $n$. In the first small training horizon case, our lower bounds almost tightly match and provide the first optimal certificates for the corresponding upper bounds. However, for the realizable case with $T = \Omega(n)$, a gap exists between the lower and upper bounds. We provide a conjecture to address this problem, that the gap can be closed by improving upper bounds, which is supported by our analyses in one-dimensional and linear regression scenarios.
Predictive Inference with Feature Conformal Prediction
Oct 01, 2022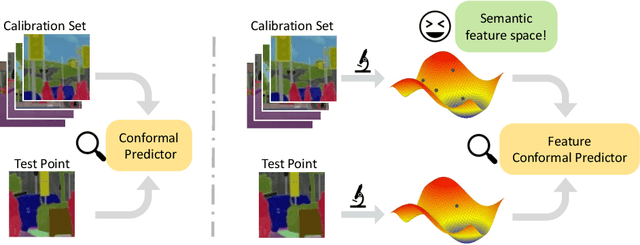

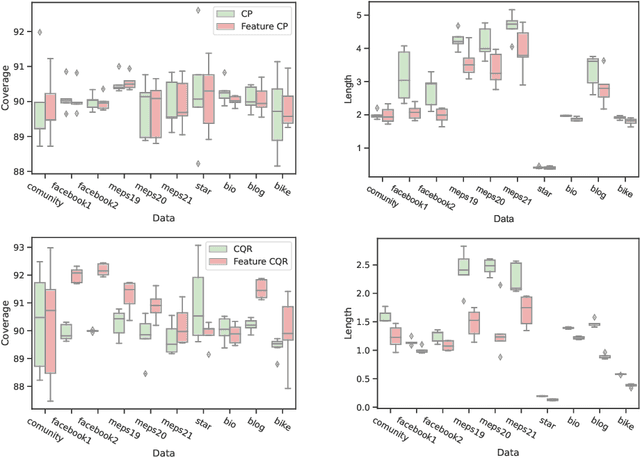
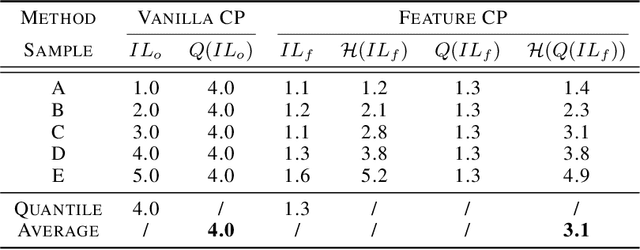
Abstract:Conformal prediction is a distribution-free technique for establishing valid prediction intervals. Although conventionally people conduct conformal prediction in the output space, this is not the only possibility. In this paper, we propose feature conformal prediction, which extends the scope of conformal prediction to semantic feature spaces by leveraging the inductive bias of deep representation learning. From a theoretical perspective, we demonstrate that feature conformal prediction provably outperforms regular conformal prediction under mild assumptions. Our approach could be combined with not only vanilla conformal prediction, but also other adaptive conformal prediction methods. Experiments on various predictive inference tasks corroborate the efficacy of our method.
Fighting Fire with Fire: Avoiding DNN Shortcuts through Priming
Jun 22, 2022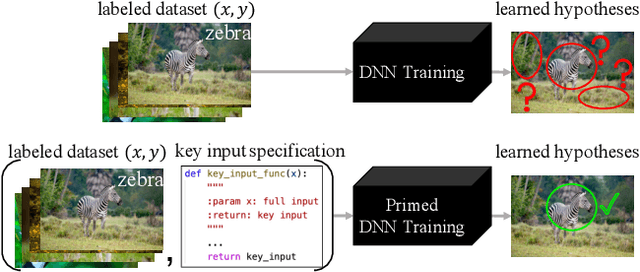

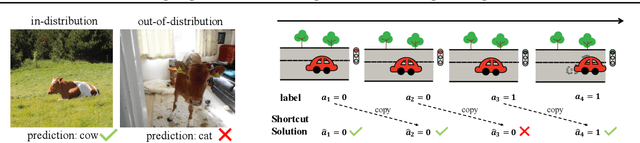
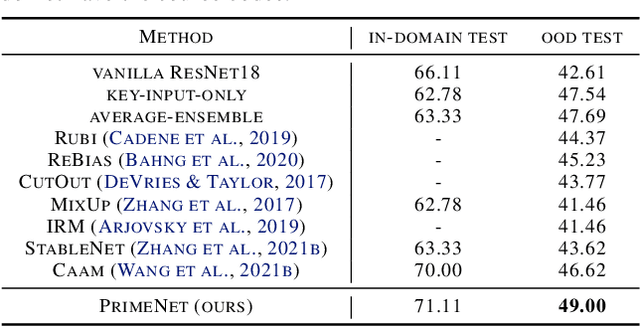
Abstract:Across applications spanning supervised classification and sequential control, deep learning has been reported to find "shortcut" solutions that fail catastrophically under minor changes in the data distribution. In this paper, we show empirically that DNNs can be coaxed to avoid poor shortcuts by providing an additional "priming" feature computed from key input features, usually a coarse output estimate. Priming relies on approximate domain knowledge of these task-relevant key input features, which is often easy to obtain in practical settings. For example, one might prioritize recent frames over past frames in a video input for visual imitation learning, or salient foreground over background pixels for image classification. On NICO image classification, MuJoCo continuous control, and CARLA autonomous driving, our priming strategy works significantly better than several popular state-of-the-art approaches for feature selection and data augmentation. We connect these empirical findings to recent theoretical results on DNN optimization, and argue theoretically that priming distracts the optimizer away from poor shortcuts by creating better, simpler shortcuts.
Anomaly Detection with Test Time Augmentation and Consistency Evaluation
Jun 06, 2022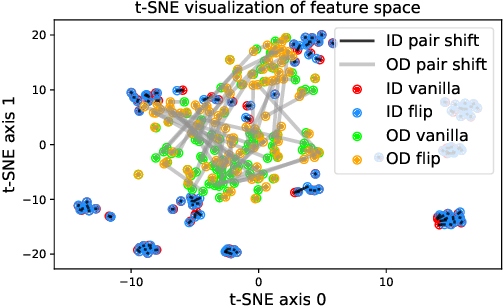
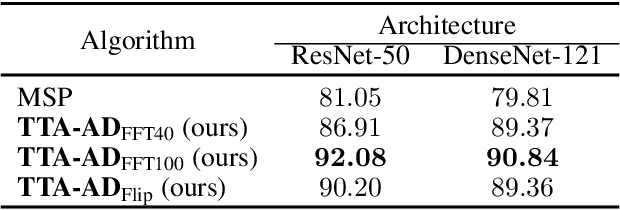

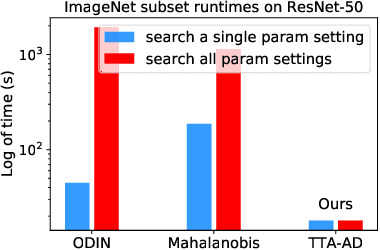
Abstract:Deep neural networks are known to be vulnerable to unseen data: they may wrongly assign high confidence stcores to out-distribuion samples. Recent works try to solve the problem using representation learning methods and specific metrics. In this paper, we propose a simple, yet effective post-hoc anomaly detection algorithm named Test Time Augmentation Anomaly Detection (TTA-AD), inspired by a novel observation. Specifically, we observe that in-distribution data enjoy more consistent predictions for its original and augmented versions on a trained network than out-distribution data, which separates in-distribution and out-distribution samples. Experiments on various high-resolution image benchmark datasets demonstrate that TTA-AD achieves comparable or better detection performance under dataset-vs-dataset anomaly detection settings with a 60%~90\% running time reduction of existing classifier-based algorithms. We provide empirical verification that the key to TTA-AD lies in the remaining classes between augmented features, which has long been partially ignored by previous works. Additionally, we use RUNS as a surrogate to analyze our algorithm theoretically.
Realistic Deep Learning May Not Fit Benignly
Jun 01, 2022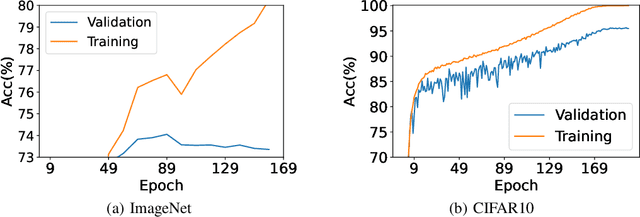
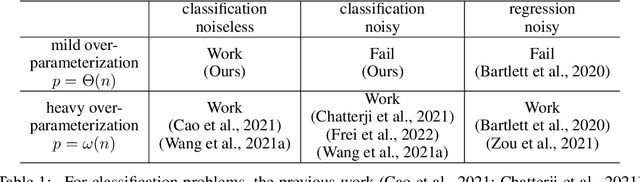
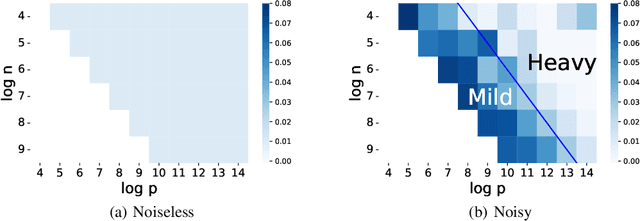
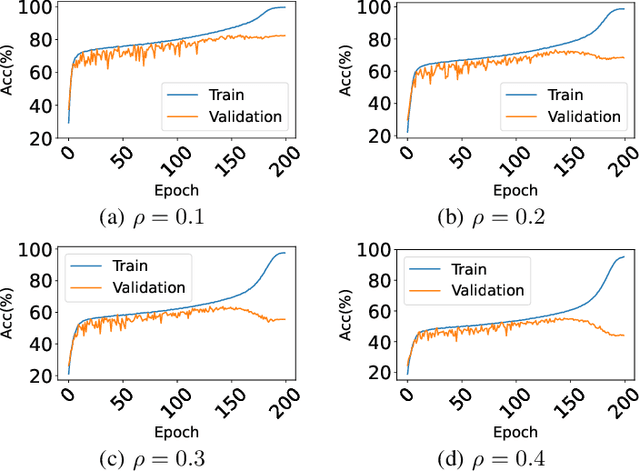
Abstract:Studies on benign overfitting provide insights for the success of overparameterized deep learning models. In this work, we examine the benign overfitting phenomena in real-world settings. We found that for tasks such as training a ResNet model on ImageNet dataset, the model does not fit benignly. To understand why benign overfitting fails in the ImageNet experiment, we analyze previous benign overfitting models under a more restrictive setup where the number of parameters is not significantly larger than the number of data points. Under this mild overparameterization setup, our analysis identifies a phase change: unlike in the heavy overparameterization setting, benign overfitting can now fail in the presence of label noise. Our study explains our empirical observations, and naturally leads to a simple technique known as self-training that can boost the model's generalization performances. Furthermore, our work highlights the importance of understanding implicit bias in underfitting regimes as a future direction.
Relaxing the Feature Covariance Assumption: Time-Variant Bounds for Benign Overfitting in Linear Regression
Feb 12, 2022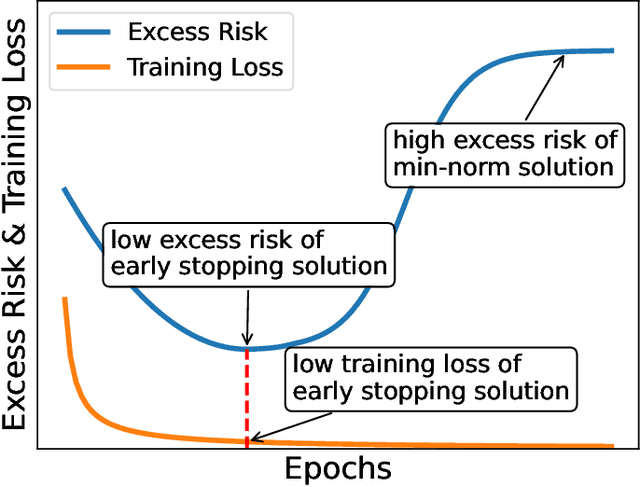
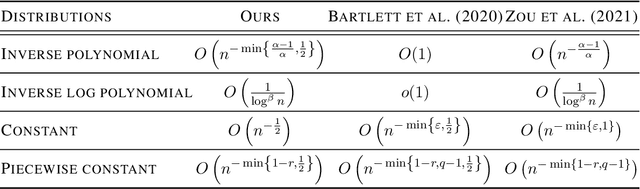
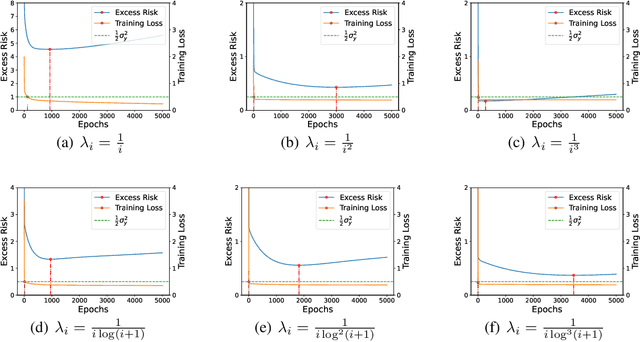
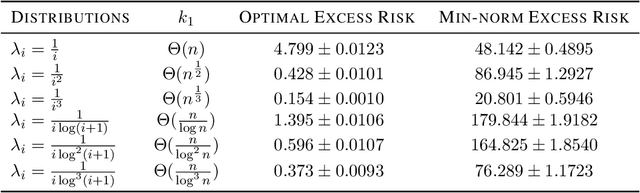
Abstract:Benign overfitting demonstrates that overparameterized models can perform well on test data while fitting noisy training data. However, it only considers the final min-norm solution in linear regression, which ignores the algorithm information and the corresponding training procedure. In this paper, we generalize the idea of benign overfitting to the whole training trajectory instead of the min-norm solution and derive a time-variant bound based on the trajectory analysis. Starting from the time-variant bound, we further derive a time interval that suffices to guarantee a consistent generalization error for a given feature covariance. Unlike existing approaches, the newly proposed generalization bound is characterized by a time-variant effective dimension of feature covariance. By introducing the time factor, we relax the strict assumption on the feature covariance matrix required in previous benign overfitting under the regimes of overparameterized linear regression with gradient descent. This paper extends the scope of benign overfitting, and experiment results indicate that the proposed bound accords better with empirical evidence.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge