Doubly Adaptive Scaled Algorithm for Machine Learning Using Second-Order Information

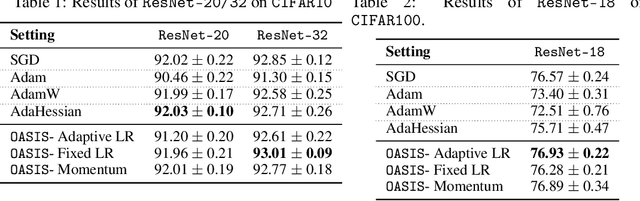
We present a novel adaptive optimization algorithm for large-scale machine learning problems. Equipped with a low-cost estimate of local curvature and Lipschitz smoothness, our method dynamically adapts the search direction and step-size. The search direction contains gradient information preconditioned by a well-scaled diagonal preconditioning matrix that captures the local curvature information. Our methodology does not require the tedious task of learning rate tuning, as the learning rate is updated automatically without adding an extra hyperparameter. We provide convergence guarantees on a comprehensive collection of optimization problems, including convex, strongly convex, and nonconvex problems, in both deterministic and stochastic regimes. We also conduct an extensive empirical evaluation on standard machine learning problems, justifying our algorithm's versatility and demonstrating its strong performance compared to other start-of-the-art first-order and second-order methods.

Scaling Up Quasi-Newton Algorithms: Communication Efficient Distributed SR1

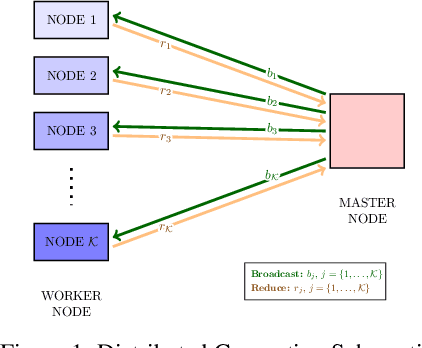
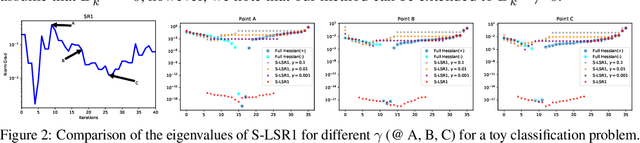
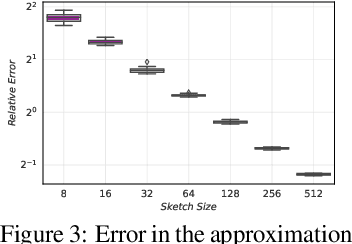
In this paper, we present a scalable distributed implementation of the sampled LSR1 (S-LSR1) algorithm. First, we show that a naive distributed implementation of S-LSR1 requires multiple rounds of expensive communications at every iteration and thus is inefficient. We then propose DS-LSR1, a communication-efficient variant of the S-LSR1 method, that drastically reduces the amount of data communicated at every iteration, that has favorable work-load balancing across nodes and that is matrix-free and inverse-free. The proposed method scales well in terms of both the dimension of the problem and the number of data points. Finally, we illustrate the performance of DS-LSR1 on standard neural network training tasks.