AttendLight: Universal Attention-Based Reinforcement Learning Model for Traffic Signal Control

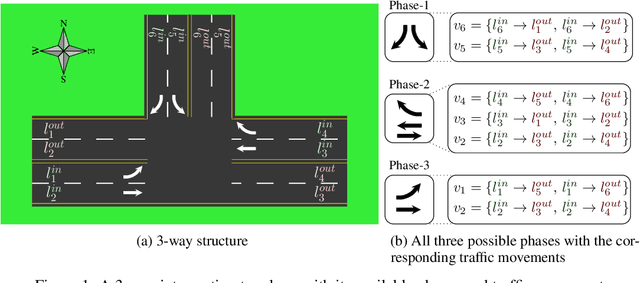
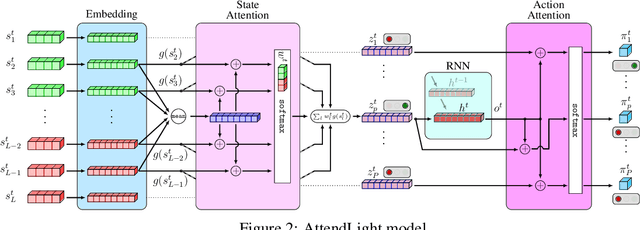
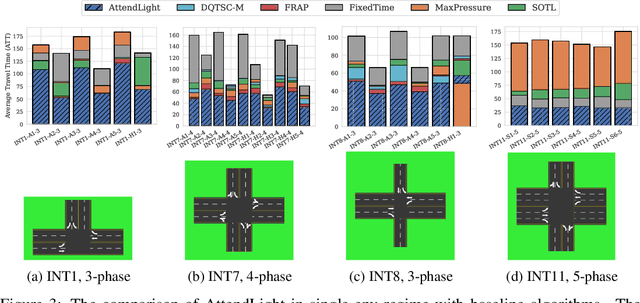
We propose AttendLight, an end-to-end Reinforcement Learning (RL) algorithm for the problem of traffic signal control. Previous approaches for this problem have the shortcoming that they require training for each new intersection with a different structure or traffic flow distribution. AttendLight solves this issue by training a single, universal model for intersections with any number of roads, lanes, phases (possible signals), and traffic flow. To this end, we propose a deep RL model which incorporates two attention models. The first attention model is introduced to handle different numbers of roads-lanes; and the second attention model is intended for enabling decision-making with any number of phases in an intersection. As a result, our proposed model works for any intersection configuration, as long as a similar configuration is represented in the training set. Experiments were conducted with both synthetic and real-world standard benchmark data-sets. The results we show cover intersections with three or four approaching roads; one-directional/bi-directional roads with one, two, and three lanes; different number of phases; and different traffic flows. We consider two regimes: (i) single-environment training, single-deployment, and (ii) multi-environment training, multi-deployment. AttendLight outperforms both classical and other RL-based approaches on all cases in both regimes.

SONIA: A Symmetric Blockwise Truncated Optimization Algorithm

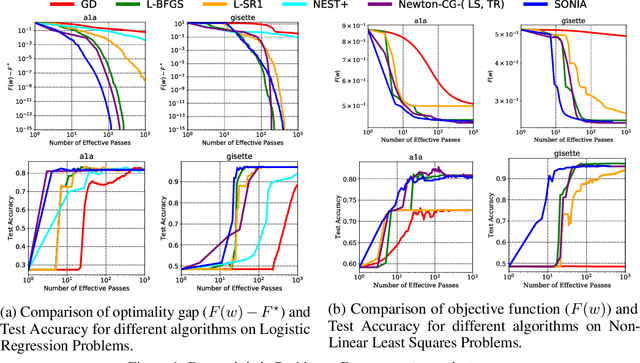
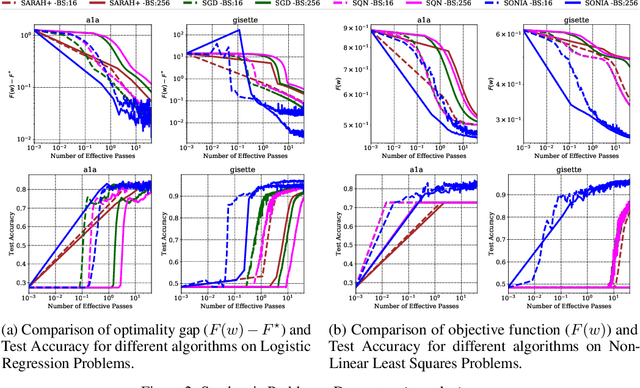
This work presents a new algorithm for empirical risk minimization. The algorithm bridges the gap between first- and second-order methods by computing a search direction that uses a second-order-type update in one subspace, coupled with a scaled steepest descent step in the orthogonal complement. To this end, partial curvature information is incorporated to help with ill-conditioning, while simultaneously allowing the algorithm to scale to the large problem dimensions often encountered in machine learning applications. Theoretical results are presented to confirm that the algorithm converges to a stationary point in both the strongly convex and nonconvex cases. A stochastic variant of the algorithm is also presented, along with corresponding theoretical guarantees. Numerical results confirm the strengths of the new approach on standard machine learning problems.

Scaling Up Quasi-Newton Algorithms: Communication Efficient Distributed SR1

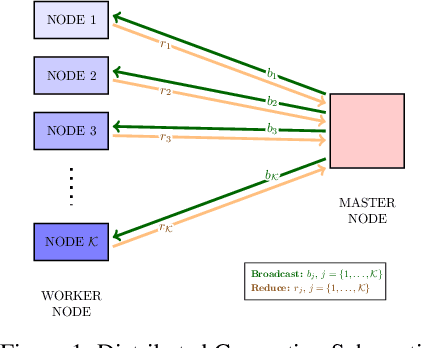
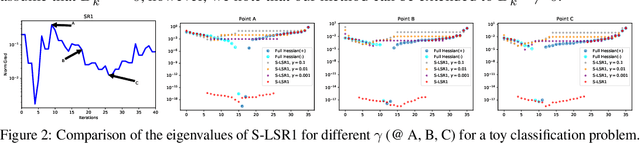
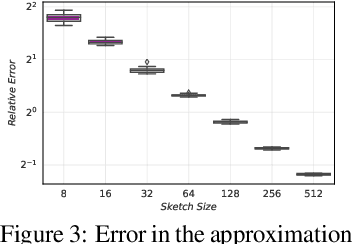
In this paper, we present a scalable distributed implementation of the sampled LSR1 (S-LSR1) algorithm. First, we show that a naive distributed implementation of S-LSR1 requires multiple rounds of expensive communications at every iteration and thus is inefficient. We then propose DS-LSR1, a communication-efficient variant of the S-LSR1 method, that drastically reduces the amount of data communicated at every iteration, that has favorable work-load balancing across nodes and that is matrix-free and inverse-free. The proposed method scales well in terms of both the dimension of the problem and the number of data points. Finally, we illustrate the performance of DS-LSR1 on standard neural network training tasks.

Don't Forget Your Teacher: A Corrective Reinforcement Learning Framework

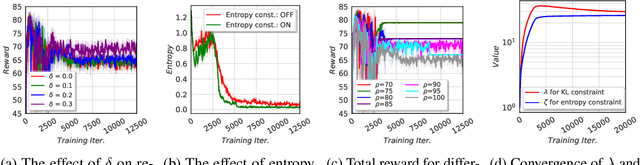
Although reinforcement learning (RL) can provide reliable solutions in many settings, practitioners are often wary of the discrepancies between the RL solution and their status quo procedures. Therefore, they may be reluctant to adapt to the novel way of executing tasks proposed by RL. On the other hand, many real-world problems require relatively small adjustments from the status quo policies to achieve improved performance. Therefore, we propose a student-teacher RL mechanism in which the RL (the "student") learns to maximize its reward, subject to a constraint that bounds the difference between the RL policy and the "teacher" policy. The teacher can be another RL policy (e.g., trained under a slightly different setting), the status quo policy, or any other exogenous policy. We formulate this problem using a stochastic optimization model and solve it using a primal-dual policy gradient algorithm. We prove that the policy is asymptotically optimal. However, a naive implementation suffers from high variance and convergence to a stochastic optimal policy. With a few practical adjustments to address these issues, our numerical experiments confirm the effectiveness of our proposed method in multiple GridWorld scenarios.

Multi-Agent Image Classification via Reinforcement Learning

We investigate a classification problem using multiple mobile agents that are capable of collecting (partial) pose-dependent observations of an unknown environment. The objective is to classify an image (e.g, map of a large area) over a finite time horizon. We propose a network architecture on how agents should form a local belief, take local actions, extract relevant features and specification from their raw partial observations. Agents are allowed to exchange information with their neighboring agents and run a decentralized consensus protocol to update their own beliefs. It is shown how reinforcement learning techniques can be utilized to achieve decentralized implementation of the classification problem. Our experimental results on MNIST handwritten digit dataset demonstrates the effectiveness of our proposed framework.

Reinforcement Learning for Solving the Vehicle Routing Problem

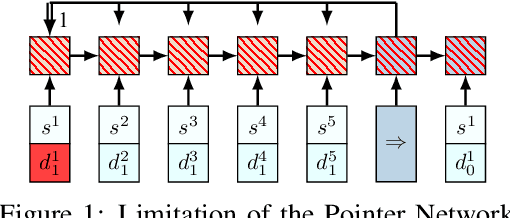
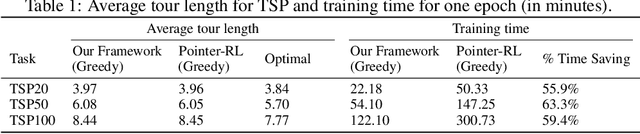
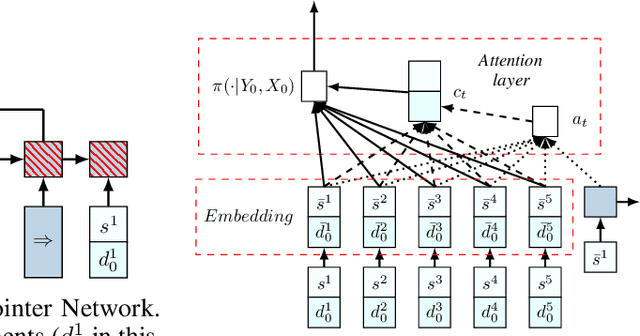
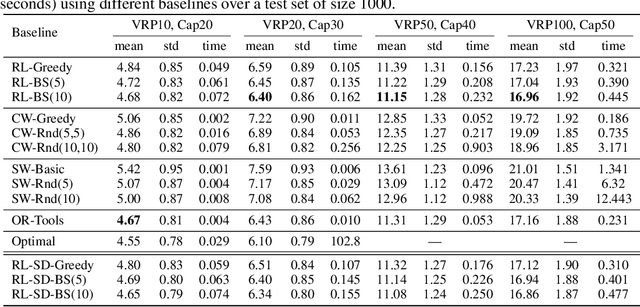
We present an end-to-end framework for solving the Vehicle Routing Problem (VRP) using reinforcement learning. In this approach, we train a single model that finds near-optimal solutions for problem instances sampled from a given distribution, only by observing the reward signals and following feasibility rules. Our model represents a parameterized stochastic policy, and by applying a policy gradient algorithm to optimize its parameters, the trained model produces the solution as a sequence of consecutive actions in real time, without the need to re-train for every new problem instance. On capacitated VRP, our approach outperforms classical heuristics and Google's OR-Tools on medium-sized instances in solution quality with comparable computation time (after training). We demonstrate how our approach can handle problems with split delivery and explore the effect of such deliveries on the solution quality. Our proposed framework can be applied to other variants of the VRP such as the stochastic VRP, and has the potential to be applied more generally to combinatorial optimization problems.