AttendLight: Universal Attention-Based Reinforcement Learning Model for Traffic Signal Control

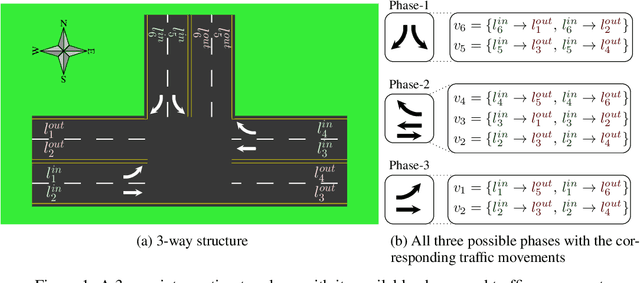
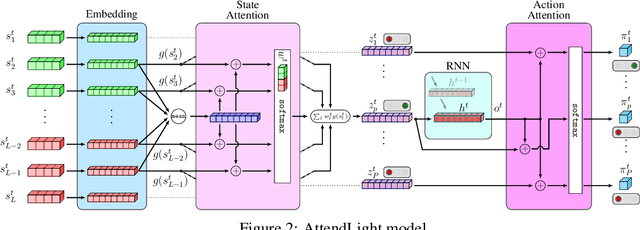
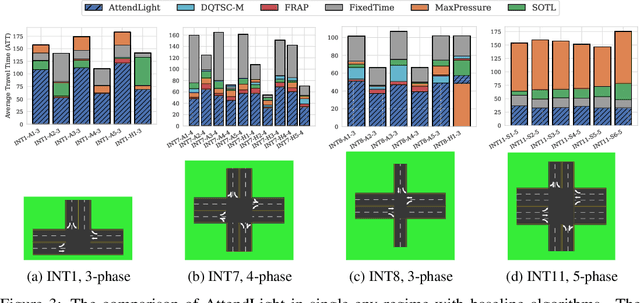
We propose AttendLight, an end-to-end Reinforcement Learning (RL) algorithm for the problem of traffic signal control. Previous approaches for this problem have the shortcoming that they require training for each new intersection with a different structure or traffic flow distribution. AttendLight solves this issue by training a single, universal model for intersections with any number of roads, lanes, phases (possible signals), and traffic flow. To this end, we propose a deep RL model which incorporates two attention models. The first attention model is introduced to handle different numbers of roads-lanes; and the second attention model is intended for enabling decision-making with any number of phases in an intersection. As a result, our proposed model works for any intersection configuration, as long as a similar configuration is represented in the training set. Experiments were conducted with both synthetic and real-world standard benchmark data-sets. The results we show cover intersections with three or four approaching roads; one-directional/bi-directional roads with one, two, and three lanes; different number of phases; and different traffic flows. We consider two regimes: (i) single-environment training, single-deployment, and (ii) multi-environment training, multi-deployment. AttendLight outperforms both classical and other RL-based approaches on all cases in both regimes.

A Review of Cooperative Multi-Agent Deep Reinforcement Learning

Deep Reinforcement Learning has made significant progress in multi-agent systems in recent years. In this review article, we have mostly focused on recent papers on Multi-Agent Reinforcement Learning (MARL) than the older papers, unless it was necessary. Several ideas and papers are proposed with different notations, and we tried our best to unify them with a single notation and categorize them by their relevance. In particular, we have focused on five common approaches on modeling and solving multi-agent reinforcement learning problems: (I) independent-learners, (II) fully observable critic, (III) value function decomposition, (IV) consensus, (IV) learn to communicate. Moreover, we discuss some new emerging research areas in MARL along with the relevant recent papers. In addition, some of the recent applications of MARL in real world are discussed. Finally, a list of available environments for MARL research are provided and the paper is concluded with proposals on the possible research directions.

Zeroth Order Nonconvex Multi-Agent Optimization over Networks

In this paper we consider distributed optimization problems over a multi-agent network, where each agent can only partially evaluate the objective function, and it is allowed to exchange messages with its immediate neighbors. Differently from all existing works on distributed optimization, our focus is given to optimizing a class of difficult non-convex problems, and under the challenging setting where each agent can only access the zeroth-order information (i.e., the functional values) of its local functions. For different types of network topologies such as undirected connected networks or star networks, we develop efficient distributed algorithms and rigorously analyze their convergence and rate of convergence (to the set of stationary solutions). Numerical results are provided to demonstrate the efficiency of the proposed algorithms.

NESTT: A Nonconvex Primal-Dual Splitting Method for Distributed and Stochastic Optimization

We study a stochastic and distributed algorithm for nonconvex problems whose objective consists of a sum of $N$ nonconvex $L_i/N$-smooth functions, plus a nonsmooth regularizer. The proposed NonconvEx primal-dual SpliTTing (NESTT) algorithm splits the problem into $N$ subproblems, and utilizes an augmented Lagrangian based primal-dual scheme to solve it in a distributed and stochastic manner. With a special non-uniform sampling, a version of NESTT achieves $\epsilon$-stationary solution using $\mathcal{O}((\sum_{i=1}^N\sqrt{L_i/N})^2/\epsilon)$ gradient evaluations, which can be up to $\mathcal{O}(N)$ times better than the (proximal) gradient descent methods. It also achieves Q-linear convergence rate for nonconvex $\ell_1$ penalized quadratic problems with polyhedral constraints. Further, we reveal a fundamental connection between primal-dual based methods and a few primal only methods such as IAG/SAG/SAGA.