Gradient-enhanced deep Gaussian processes for multifidelity modelling

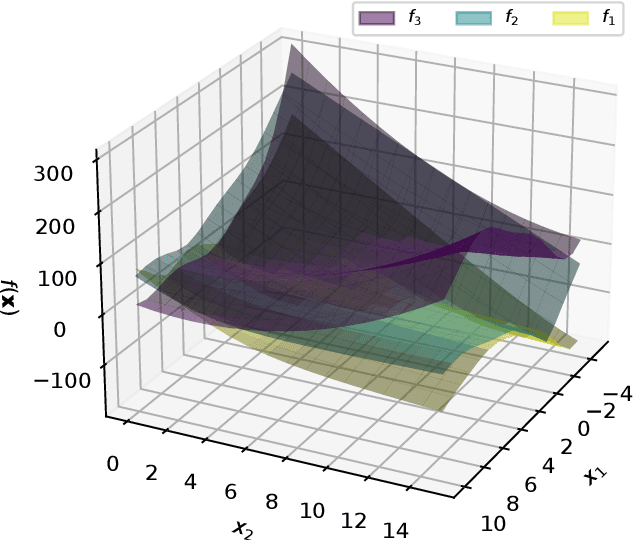
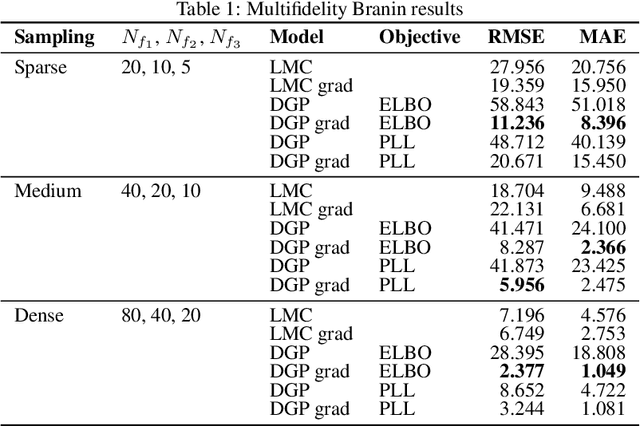
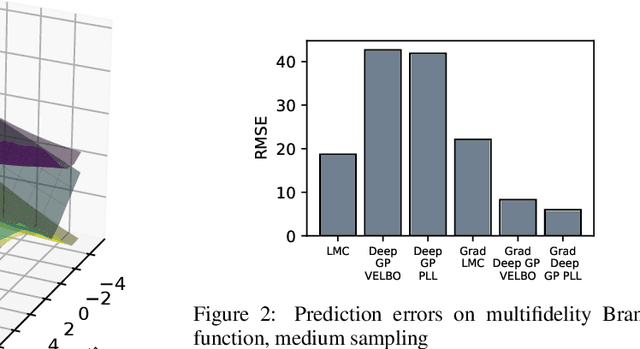
Multifidelity models integrate data from multiple sources to produce a single approximator for the underlying process. Dense low-fidelity samples are used to reduce interpolation error, while sparse high-fidelity samples are used to compensate for bias or noise in the low-fidelity samples. Deep Gaussian processes (GPs) are attractive for multifidelity modelling as they are non-parametric, robust to overfitting, perform well for small datasets, and, critically, can capture nonlinear and input-dependent relationships between data of different fidelities. Many datasets naturally contain gradient data, especially when they are generated by computational models that are compatible with automatic differentiation or have adjoint solutions. Principally, this work extends deep GPs to incorporate gradient data. We demonstrate this method on an analytical test problem and a realistic partial differential equation problem, where we predict the aerodynamic coefficients of a hypersonic flight vehicle over a range of flight conditions and geometries. In both examples, the gradient-enhanced deep GP outperforms a gradient-enhanced linear GP model and their non-gradient-enhanced counterparts.

Neural network architectures using min plus algebra for solving certain high dimensional optimal control problems and Hamilton-Jacobi PDEs

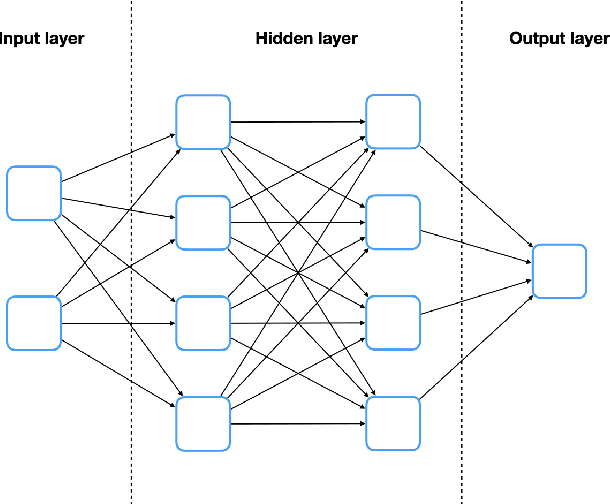
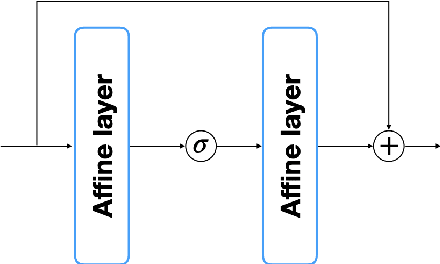
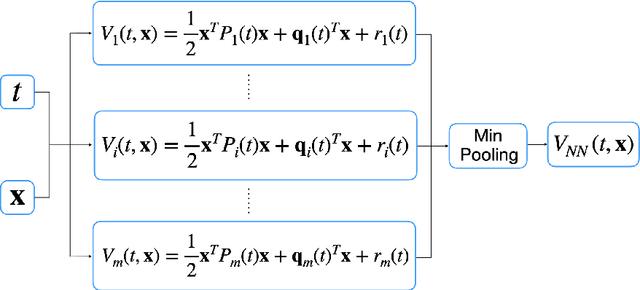
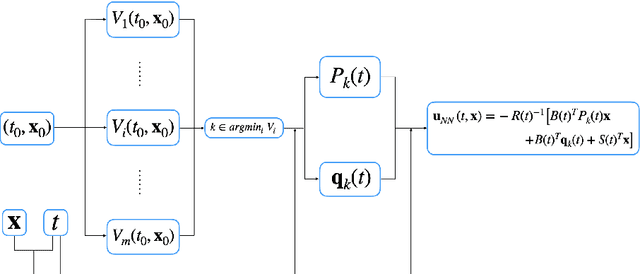
Solving high dimensional optimal control problems and corresponding Hamilton-Jacobi PDEs are important but challenging problems in control engineering. In this paper, we propose two abstract neural network architectures which respectively represent the value function and the state feedback characterisation of the optimal control for certain class of high dimensional optimal control problems. We provide the mathematical analysis for the two abstract architectures. We also show several numerical results computed using the deep neural network implementations of these abstract architectures. This work paves the way to leverage efficient dedicated hardware designed for neural networks to solve high dimensional optimal control problems and Hamilton-Jacobi PDEs.