HJ-sampler: A Bayesian sampler for inverse problems of a stochastic process by leveraging Hamilton-Jacobi PDEs and score-based generative models

The interplay between stochastic processes and optimal control has been extensively explored in the literature. With the recent surge in the use of diffusion models, stochastic processes have increasingly been applied to sample generation. This paper builds on the log transform, known as the Cole-Hopf transform in Brownian motion contexts, and extends it within a more abstract framework that includes a linear operator. Within this framework, we found that the well-known relationship between the Cole-Hopf transform and optimal transport is a particular instance where the linear operator acts as the infinitesimal generator of a stochastic process. We also introduce a novel scenario where the linear operator is the adjoint of the generator, linking to Bayesian inference under specific initial and terminal conditions. Leveraging this theoretical foundation, we develop a new algorithm, named the HJ-sampler, for Bayesian inference for the inverse problem of a stochastic differential equation with given terminal observations. The HJ-sampler involves two stages: (1) solving the viscous Hamilton-Jacobi partial differential equations, and (2) sampling from the associated stochastic optimal control problem. Our proposed algorithm naturally allows for flexibility in selecting the numerical solver for viscous HJ PDEs. We introduce two variants of the solver: the Riccati-HJ-sampler, based on the Riccati method, and the SGM-HJ-sampler, which utilizes diffusion models. We demonstrate the effectiveness and flexibility of the proposed methods by applying them to solve Bayesian inverse problems involving various stochastic processes and prior distributions, including applications that address model misspecifications and quantifying model uncertainty.

Leveraging viscous Hamilton-Jacobi PDEs for uncertainty quantification in scientific machine learning

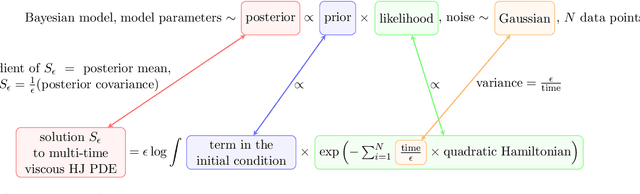
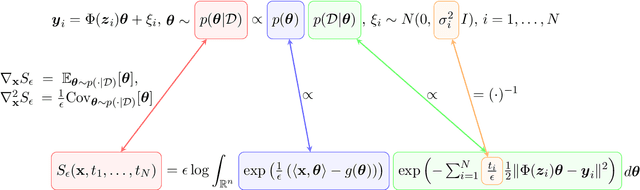
Uncertainty quantification (UQ) in scientific machine learning (SciML) combines the powerful predictive power of SciML with methods for quantifying the reliability of the learned models. However, two major challenges remain: limited interpretability and expensive training procedures. We provide a new interpretation for UQ problems by establishing a new theoretical connection between some Bayesian inference problems arising in SciML and viscous Hamilton-Jacobi partial differential equations (HJ PDEs). Namely, we show that the posterior mean and covariance can be recovered from the spatial gradient and Hessian of the solution to a viscous HJ PDE. As a first exploration of this connection, we specialize to Bayesian inference problems with linear models, Gaussian likelihoods, and Gaussian priors. In this case, the associated viscous HJ PDEs can be solved using Riccati ODEs, and we develop a new Riccati-based methodology that provides computational advantages when continuously updating the model predictions. Specifically, our Riccati-based approach can efficiently add or remove data points to the training set invariant to the order of the data and continuously tune hyperparameters. Moreover, neither update requires retraining on or access to previously incorporated data. We provide several examples from SciML involving noisy data and \textit{epistemic uncertainty} to illustrate the potential advantages of our approach. In particular, this approach's amenability to data streaming applications demonstrates its potential for real-time inferences, which, in turn, allows for applications in which the predicted uncertainty is used to dynamically alter the learning process.

Efficient first-order algorithms for large-scale, non-smooth maximum entropy models with application to wildfire science

Maximum entropy (Maxent) models are a class of statistical models that use the maximum entropy principle to estimate probability distributions from data. Due to the size of modern data sets, Maxent models need efficient optimization algorithms to scale well for big data applications. State-of-the-art algorithms for Maxent models, however, were not originally designed to handle big data sets; these algorithms either rely on technical devices that may yield unreliable numerical results, scale poorly, or require smoothness assumptions that many practical Maxent models lack. In this paper, we present novel optimization algorithms that overcome the shortcomings of state-of-the-art algorithms for training large-scale, non-smooth Maxent models. Our proposed first-order algorithms leverage the Kullback-Leibler divergence to train large-scale and non-smooth Maxent models efficiently. For Maxent models with discrete probability distribution of $n$ elements built from samples, each containing $m$ features, the stepsize parameters estimation and iterations in our algorithms scale on the order of $O(mn)$ operations and can be trivially parallelized. Moreover, the strong $\ell_{1}$ convexity of the Kullback--Leibler divergence allows for larger stepsize parameters, thereby speeding up the convergence rate of our algorithms. To illustrate the efficiency of our novel algorithms, we consider the problem of estimating probabilities of fire occurrences as a function of ecological features in the Western US MTBS-Interagency wildfire data set. Our numerical results show that our algorithms outperform the state of the arts by one order of magnitude and yield results that agree with physical models of wildfire occurrence and previous statistical analyses of wildfire drivers.

Leveraging Hamilton-Jacobi PDEs with time-dependent Hamiltonians for continual scientific machine learning

We address two major challenges in scientific machine learning (SciML): interpretability and computational efficiency. We increase the interpretability of certain learning processes by establishing a new theoretical connection between optimization problems arising from SciML and a generalized Hopf formula, which represents the viscosity solution to a Hamilton-Jacobi partial differential equation (HJ PDE) with time-dependent Hamiltonian. Namely, we show that when we solve certain regularized learning problems with integral-type losses, we actually solve an optimal control problem and its associated HJ PDE with time-dependent Hamiltonian. This connection allows us to reinterpret incremental updates to learned models as the evolution of an associated HJ PDE and optimal control problem in time, where all of the previous information is intrinsically encoded in the solution to the HJ PDE. As a result, existing HJ PDE solvers and optimal control algorithms can be reused to design new efficient training approaches for SciML that naturally coincide with the continual learning framework, while avoiding catastrophic forgetting. As a first exploration of this connection, we consider the special case of linear regression and leverage our connection to develop a new Riccati-based methodology for solving these learning problems that is amenable to continual learning applications. We also provide some corresponding numerical examples that demonstrate the potential computational and memory advantages our Riccati-based approach can provide.

Leveraging Multi-time Hamilton-Jacobi PDEs for Certain Scientific Machine Learning Problems

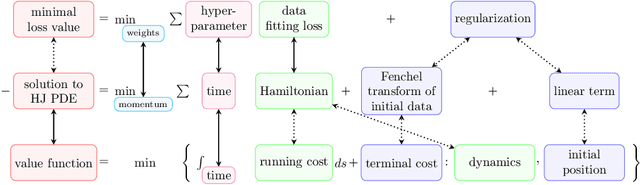
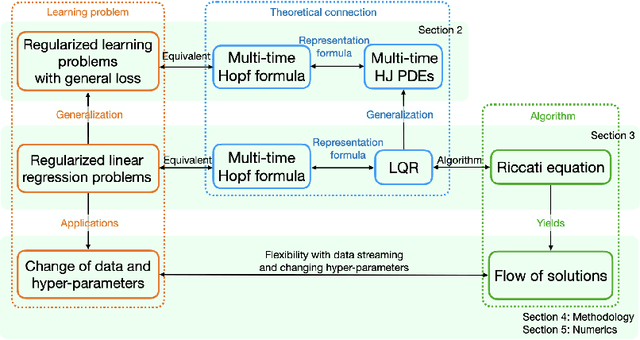
Hamilton-Jacobi partial differential equations (HJ PDEs) have deep connections with a wide range of fields, including optimal control, differential games, and imaging sciences. By considering the time variable to be a higher dimensional quantity, HJ PDEs can be extended to the multi-time case. In this paper, we establish a novel theoretical connection between specific optimization problems arising in machine learning and the multi-time Hopf formula, which corresponds to a representation of the solution to certain multi-time HJ PDEs. Through this connection, we increase the interpretability of the training process of certain machine learning applications by showing that when we solve these learning problems, we also solve a multi-time HJ PDE and, by extension, its corresponding optimal control problem. As a first exploration of this connection, we develop the relation between the regularized linear regression problem and the Linear Quadratic Regulator (LQR). We then leverage our theoretical connection to adapt standard LQR solvers (namely, those based on the Riccati ordinary differential equations) to design new training approaches for machine learning. Finally, we provide some numerical examples that demonstrate the versatility and possible computational advantages of our Riccati-based approach in the context of continual learning, post-training calibration, transfer learning, and sparse dynamics identification.

SympOCnet: Solving optimal control problems with applications to high-dimensional multi-agent path planning problems

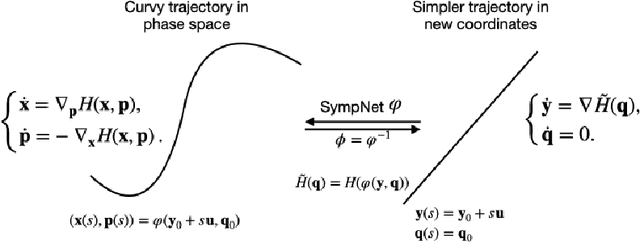
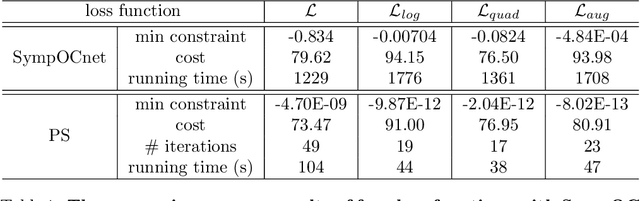
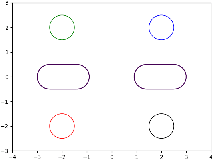
Solving high-dimensional optimal control problems in real-time is an important but challenging problem, with applications to multi-agent path planning problems, which have drawn increased attention given the growing popularity of drones in recent years. In this paper, we propose a novel neural network method called SympOCnet that applies the Symplectic network to solve high-dimensional optimal control problems with state constraints. We present several numerical results on path planning problems in two-dimensional and three-dimensional spaces. Specifically, we demonstrate that our SympOCnet can solve a problem with more than 500 dimensions in 1.5 hours on a single GPU, which shows the effectiveness and efficiency of SympOCnet. The proposed method is scalable and has the potential to solve truly high-dimensional path planning problems in real-time.

Efficient and robust high-dimensional sparse logistic regression via nonlinear primal-dual hybrid gradient algorithms

Logistic regression is a widely used statistical model to describe the relationship between a binary response variable and predictor variables in data sets. It is often used in machine learning to identify important predictor variables. This task, variable selection, typically amounts to fitting a logistic regression model regularized by a convex combination of $\ell_1$ and $\ell_{2}^{2}$ penalties. Since modern big data sets can contain hundreds of thousands to billions of predictor variables, variable selection methods depend on efficient and robust optimization algorithms to perform well. State-of-the-art algorithms for variable selection, however, were not traditionally designed to handle big data sets; they either scale poorly in size or are prone to produce unreliable numerical results. It therefore remains challenging to perform variable selection on big data sets without access to adequate and costly computational resources. In this paper, we propose a nonlinear primal-dual algorithm that addresses these shortcomings. Specifically, we propose an iterative algorithm that provably computes a solution to a logistic regression problem regularized by an elastic net penalty in $O(T(m,n)\log(1/\epsilon))$ operations, where $\epsilon \in (0,1)$ denotes the tolerance and $T(m,n)$ denotes the number of arithmetic operations required to perform matrix-vector multiplication on a data set with $m$ samples each comprising $n$ features. This result improves on the known complexity bound of $O(\min(m^2n,mn^2)\log(1/\epsilon))$ for first-order optimization methods such as the classic primal-dual hybrid gradient or forward-backward splitting methods.

Accelerated nonlinear primal-dual hybrid gradient algorithms with applications to machine learning

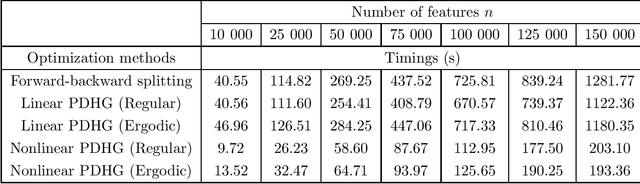
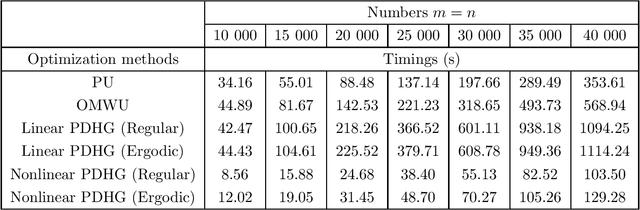
The primal-dual hybrid gradient (PDHG) algorithm is a first-order method that splits convex optimization problems with saddle-point structure into smaller subproblems. Those subproblems, unlike those obtained from most other splitting methods, can generally be solved efficiently because they involve simple operations such as matrix-vector multiplications or proximal mappings that are easy to evaluate. In order to work fast, however, the PDHG algorithm requires stepsize parameters fine-tuned for the problem at hand. Unfortunately, the stepsize parameters must often be estimated from quantities that are prohibitively expensive to compute for large-scale optimization problems, such as those in machine learning. In this paper, we introduce accelerated nonlinear variants of the PDHG algorithm that can achieve, for a broad class of optimization problems relevant to machine learning, an optimal rate of convergence with stepsize parameters that are simple to compute. We prove rigorous convergence results, including for problems posed on infinite-dimensional reflexive Banach spaces. We also provide practical implementations of accelerated nonlinear PDHG algorithms for solving several regression tasks in machine learning, including support vector machines without offset, kernel ridge regression, elastic net regularized linear regression, and the least absolute shrinkage selection operator.

On Hamilton-Jacobi PDEs and image denoising models with certain non-additive noise

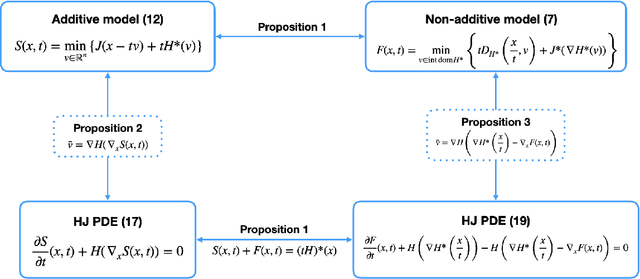
We consider image denoising problems formulated as variational problems. It is known that Hamilton-Jacobi PDEs govern the solution of such optimization problems when the noise model is additive. In this work, we address certain non-additive noise models and show that they are also related to Hamilton-Jacobi PDEs. These findings allow us to establish new connections between additive and non-additive noise imaging models. With these connections, some non-convex models for non-additive noise can be solved by applying convex optimization algorithms to the equivalent convex models for additive noise. Several numerical results are provided for denoising problems with Poisson noise or multiplicative noise.

Neural network architectures using min plus algebra for solving certain high dimensional optimal control problems and Hamilton-Jacobi PDEs

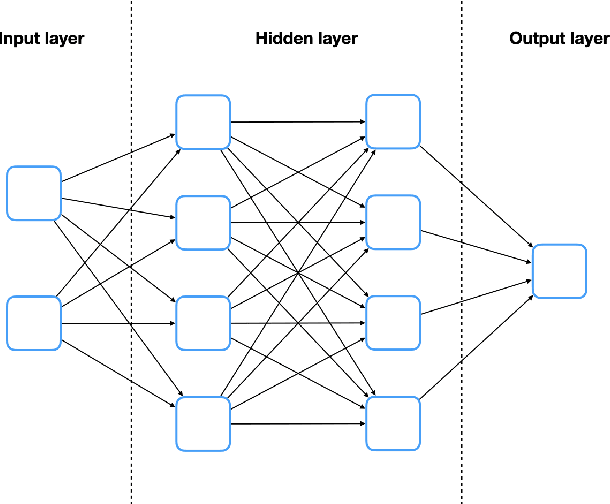
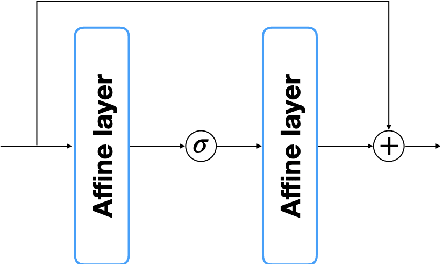
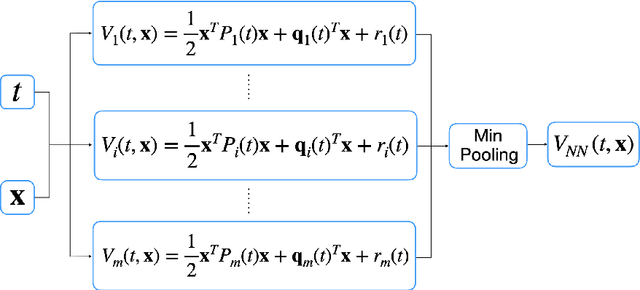
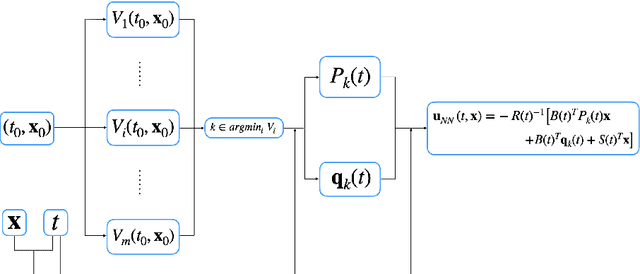
Solving high dimensional optimal control problems and corresponding Hamilton-Jacobi PDEs are important but challenging problems in control engineering. In this paper, we propose two abstract neural network architectures which respectively represent the value function and the state feedback characterisation of the optimal control for certain class of high dimensional optimal control problems. We provide the mathematical analysis for the two abstract architectures. We also show several numerical results computed using the deep neural network implementations of these abstract architectures. This work paves the way to leverage efficient dedicated hardware designed for neural networks to solve high dimensional optimal control problems and Hamilton-Jacobi PDEs.