Neural network architectures using min plus algebra for solving certain high dimensional optimal control problems and Hamilton-Jacobi PDEs
Paper and Code
May 07, 2021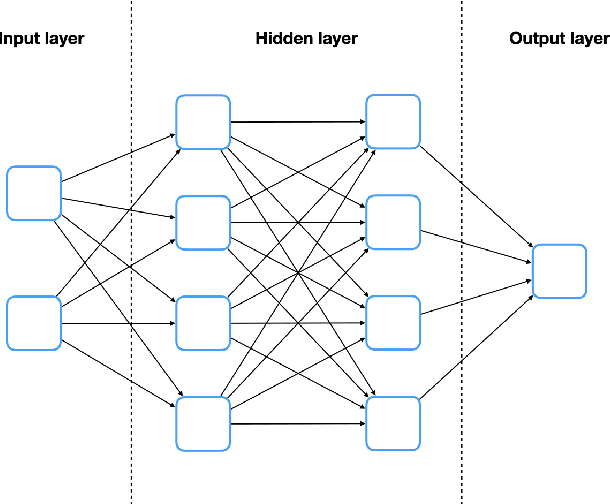
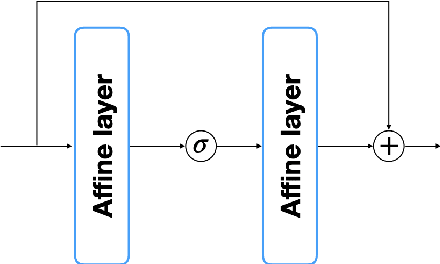
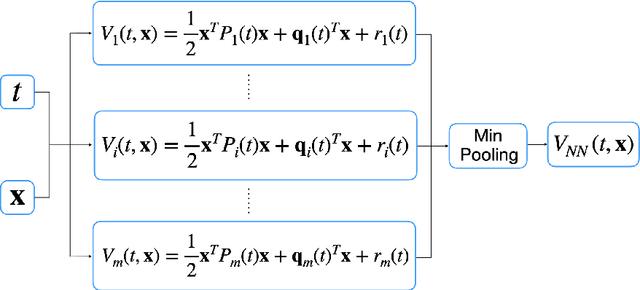
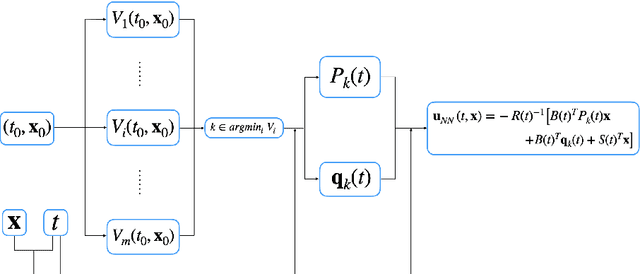
Solving high dimensional optimal control problems and corresponding Hamilton-Jacobi PDEs are important but challenging problems in control engineering. In this paper, we propose two abstract neural network architectures which respectively represent the value function and the state feedback characterisation of the optimal control for certain class of high dimensional optimal control problems. We provide the mathematical analysis for the two abstract architectures. We also show several numerical results computed using the deep neural network implementations of these abstract architectures. This work paves the way to leverage efficient dedicated hardware designed for neural networks to solve high dimensional optimal control problems and Hamilton-Jacobi PDEs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge