Accelerated nonlinear primal-dual hybrid gradient algorithms with applications to machine learning
Paper and Code
Sep 24, 2021

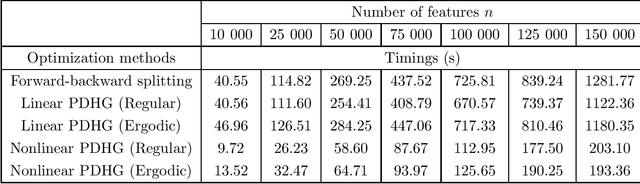
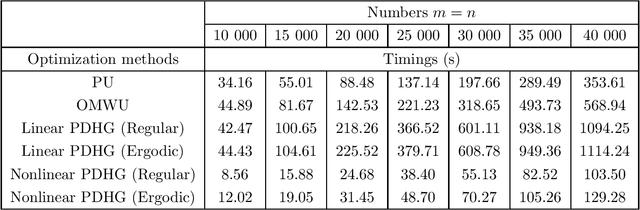
The primal-dual hybrid gradient (PDHG) algorithm is a first-order method that splits convex optimization problems with saddle-point structure into smaller subproblems. Those subproblems, unlike those obtained from most other splitting methods, can generally be solved efficiently because they involve simple operations such as matrix-vector multiplications or proximal mappings that are easy to evaluate. In order to work fast, however, the PDHG algorithm requires stepsize parameters fine-tuned for the problem at hand. Unfortunately, the stepsize parameters must often be estimated from quantities that are prohibitively expensive to compute for large-scale optimization problems, such as those in machine learning. In this paper, we introduce accelerated nonlinear variants of the PDHG algorithm that can achieve, for a broad class of optimization problems relevant to machine learning, an optimal rate of convergence with stepsize parameters that are simple to compute. We prove rigorous convergence results, including for problems posed on infinite-dimensional reflexive Banach spaces. We also provide practical implementations of accelerated nonlinear PDHG algorithms for solving several regression tasks in machine learning, including support vector machines without offset, kernel ridge regression, elastic net regularized linear regression, and the least absolute shrinkage selection operator.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge