Get our free extension to see links to code for papers anywhere online!Free add-on: code for papers everywhere!Free add-on: See code for papers anywhere!
Elena Resmerita
On Hamilton-Jacobi PDEs and image denoising models with certain non-additive noise
May 28, 2021Figures and Tables:
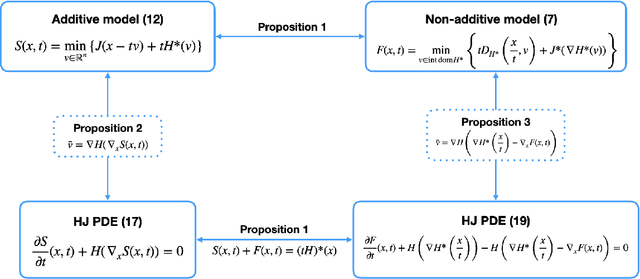






Abstract:We consider image denoising problems formulated as variational problems. It is known that Hamilton-Jacobi PDEs govern the solution of such optimization problems when the noise model is additive. In this work, we address certain non-additive noise models and show that they are also related to Hamilton-Jacobi PDEs. These findings allow us to establish new connections between additive and non-additive noise imaging models. With these connections, some non-convex models for non-additive noise can be solved by applying convex optimization algorithms to the equivalent convex models for additive noise. Several numerical results are provided for denoising problems with Poisson noise or multiplicative noise.
Via
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge