Neural Persistence Dynamics

We consider the problem of learning the dynamics in the topology of time-evolving point clouds, the prevalent spatiotemporal model for systems exhibiting collective behavior, such as swarms of insects and birds or particles in physics. In such systems, patterns emerge from (local) interactions among self-propelled entities. While several well-understood governing equations for motion and interaction exist, they are difficult to fit to data due to the often large number of entities and missing correspondences between the observation times, which may also not be equidistant. To evade such confounding factors, we investigate collective behavior from a \textit{topological perspective}, but instead of summarizing entire observation sequences (as in prior work), we propose learning a latent dynamical model from topological features \textit{per time point}. The latter is then used to formulate a downstream regression task to predict the parametrization of some a priori specified governing equation. We implement this idea based on a latent ODE learned from vectorized (static) persistence diagrams and show that this modeling choice is justified by a combination of recent stability results for persistent homology. Various (ablation) experiments not only demonstrate the relevance of each individual model component, but provide compelling empirical evidence that our proposed model -- \textit{neural persistence dynamics} -- substantially outperforms the state-of-the-art across a diverse set of parameter regression tasks.

Latent SDEs on Homogeneous Spaces

We consider the problem of variational Bayesian inference in a latent variable model where a (possibly complex) observed stochastic process is governed by the solution of a latent stochastic differential equation (SDE). Motivated by the challenges that arise when trying to learn an (almost arbitrary) latent neural SDE from large-scale data, such as efficient gradient computation, we take a step back and study a specific subclass instead. In our case, the SDE evolves on a homogeneous latent space and is induced by stochastic dynamics of the corresponding (matrix) Lie group. In learning problems, SDEs on the unit $n$-sphere are arguably the most relevant incarnation of this setup. Notably, for variational inference, the sphere not only facilitates using a truly uninformative prior SDE, but we also obtain a particularly simple and intuitive expression for the Kullback-Leibler divergence between the approximate posterior and prior process in the evidence lower bound. Experiments demonstrate that a latent SDE of the proposed type can be learned efficiently by means of an existing one-step geometric Euler-Maruyama scheme. Despite restricting ourselves to a less diverse class of SDEs, we achieve competitive or even state-of-the-art performance on various time series interpolation and classification benchmarks.

On Measuring Excess Capacity in Neural Networks

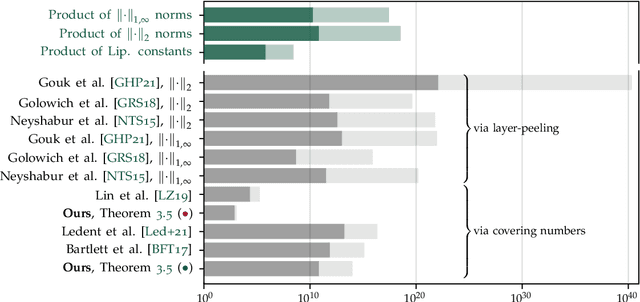
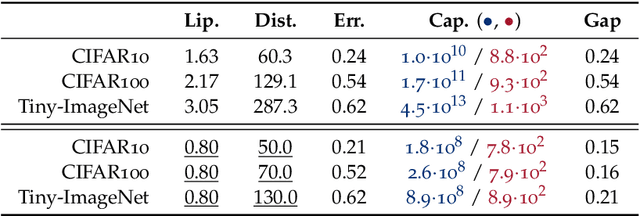
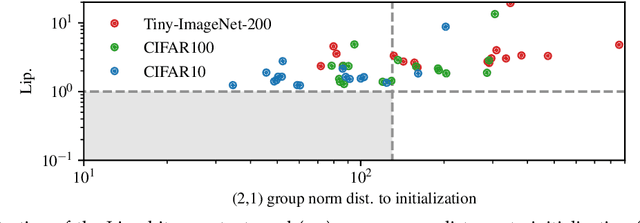
We study the excess capacity of deep networks in the context of supervised classification. That is, given a capacity measure of the underlying hypothesis class -- in our case, Rademacher complexity -- how much can we (a-priori) constrain this class while maintaining an empirical error comparable to the unconstrained setting. To assess excess capacity in modern architectures, we first extend an existing generalization bound to accommodate function composition and addition, as well as the specific structure of convolutions. This then facilitates studying residual networks through the lens of the accompanying capacity measure. The key quantities driving this measure are the Lipschitz constants of the layers and the (2,1) group norm distance to the initializations of the convolution weights. We show that these quantities (1) can be kept surprisingly small and, (2) since excess capacity unexpectedly increases with task difficulty, this points towards an unnecessarily large capacity of unconstrained models.

Topological Attention for Time Series Forecasting

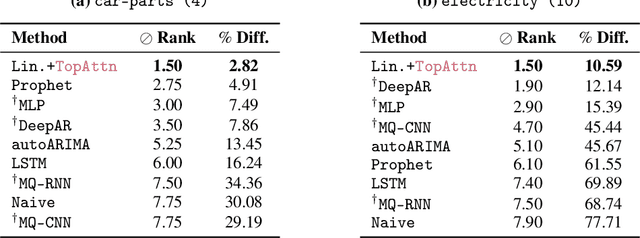
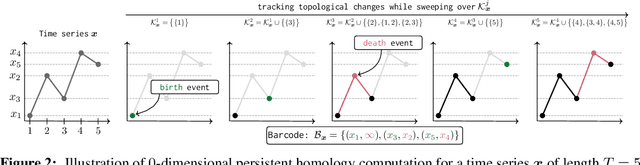
The problem of (point) forecasting $ \textit{univariate} $ time series is considered. Most approaches, ranging from traditional statistical methods to recent learning-based techniques with neural networks, directly operate on raw time series observations. As an extension, we study whether $\textit{local topological properties}$, as captured via persistent homology, can serve as a reliable signal that provides complementary information for learning to forecast. To this end, we propose $\textit{topological attention}$, which allows attending to local topological features within a time horizon of historical data. Our approach easily integrates into existing end-to-end trainable forecasting models, such as $\texttt{N-BEATS}$, and in combination with the latter exhibits state-of-the-art performance on the large-scale M4 benchmark dataset of 100,000 diverse time series from different domains. Ablation experiments, as well as a comparison to a broad range of forecasting methods in a setting where only a single time series is available for training, corroborate the beneficial nature of including local topological information through an attention mechanism.

Dissecting Supervised Constrastive Learning

Minimizing cross-entropy over the softmax scores of a linear map composed with a high-capacity encoder is arguably the most popular choice for training neural networks on supervised learning tasks. However, recent works show that one can directly optimize the encoder instead, to obtain equally (or even more) discriminative representations via a supervised variant of a contrastive objective. In this work, we address the question whether there are fundamental differences in the sought-for representation geometry in the output space of the encoder at minimal loss. Specifically, we prove, under mild assumptions, that both losses attain their minimum once the representations of each class collapse to the vertices of a regular simplex, inscribed in a hypersphere. We provide empirical evidence that this configuration is attained in practice and that reaching a close-to-optimal state typically indicates good generalization performance. Yet, the two losses show remarkably different optimization behavior. The number of iterations required to perfectly fit to data scales superlinearly with the amount of randomly flipped labels for the supervised contrastive loss. This is in contrast to the approximately linear scaling previously reported for networks trained with cross-entropy.

Topologically Densified Distributions

We study regularization in the context of small sample-size learning with over-parameterized neural networks. Specifically, we shift focus from architectural properties, such as norms on the network weights, to properties of the internal representations before a linear classifier. Specifically, we impose a topological constraint on samples drawn from the probability measure induced in that space. This provably leads to mass concentration effects around the representations of training instances, i.e., a property beneficial for generalization. By leveraging previous work to impose topological constraints in a neural network setting, we provide empirical evidence (across various vision benchmarks) to support our claim for better generalization.