Christoph Hofer
Topological Attention for Time Series Forecasting
Jul 19, 2021
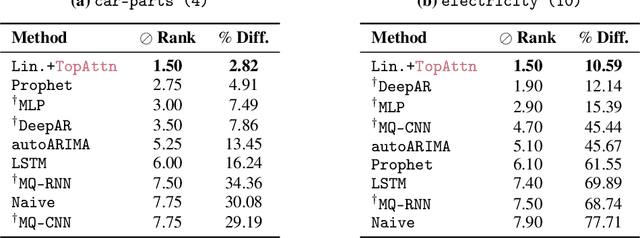
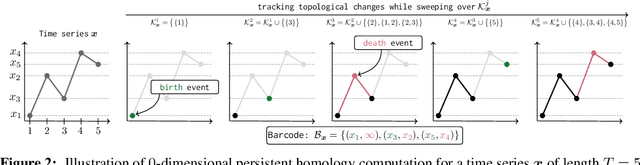

Abstract:The problem of (point) forecasting $ \textit{univariate} $ time series is considered. Most approaches, ranging from traditional statistical methods to recent learning-based techniques with neural networks, directly operate on raw time series observations. As an extension, we study whether $\textit{local topological properties}$, as captured via persistent homology, can serve as a reliable signal that provides complementary information for learning to forecast. To this end, we propose $\textit{topological attention}$, which allows attending to local topological features within a time horizon of historical data. Our approach easily integrates into existing end-to-end trainable forecasting models, such as $\texttt{N-BEATS}$, and in combination with the latter exhibits state-of-the-art performance on the large-scale M4 benchmark dataset of 100,000 diverse time series from different domains. Ablation experiments, as well as a comparison to a broad range of forecasting methods in a setting where only a single time series is available for training, corroborate the beneficial nature of including local topological information through an attention mechanism.
Connectivity-Optimized Representation Learning via Persistent Homology
Jun 21, 2019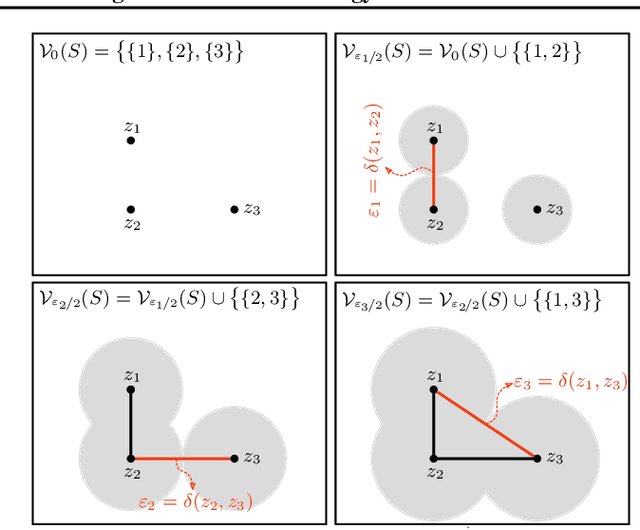
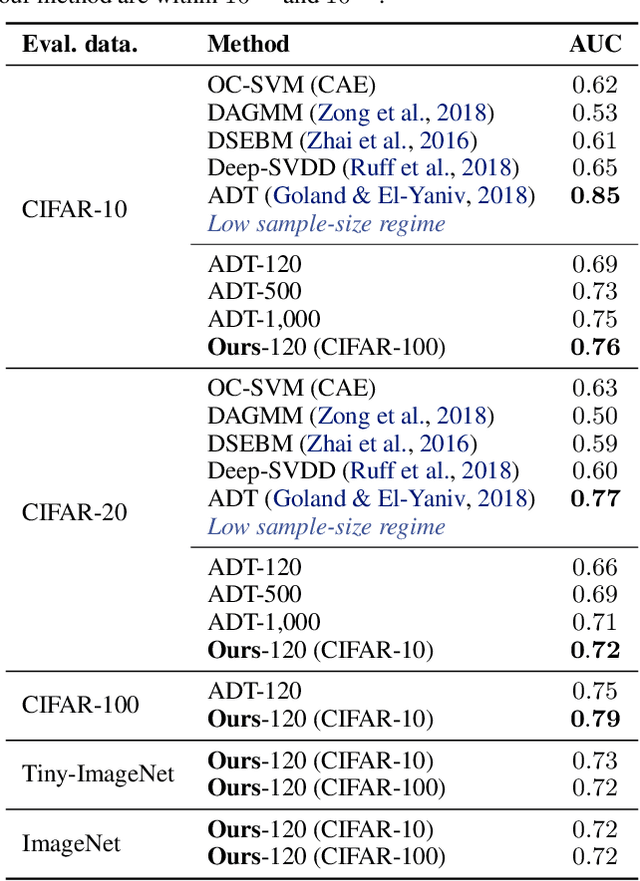
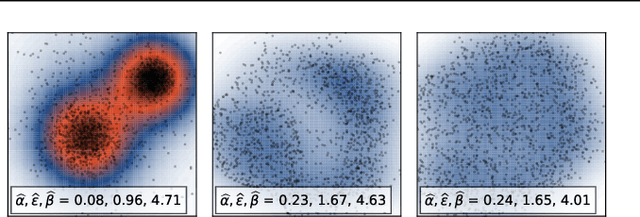
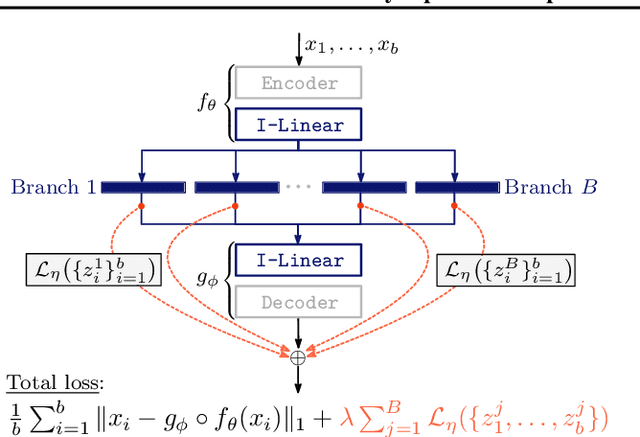
Abstract:We study the problem of learning representations with controllable connectivity properties. This is beneficial in situations when the imposed structure can be leveraged upstream. In particular, we control the connectivity of an autoencoder's latent space via a novel type of loss, operating on information from persistent homology. Under mild conditions, this loss is differentiable and we present a theoretical analysis of the properties induced by the loss. We choose one-class learning as our upstream task and demonstrate that the imposed structure enables informed parameter selection for modeling the in-class distribution via kernel density estimators. Evaluated on computer vision data, these one-class models exhibit competitive performance and, in a low sample size regime, outperform other methods by a large margin. Notably, our results indicate that a single autoencoder, trained on auxiliary (unlabeled) data, yields a mapping into latent space that can be reused across datasets for one-class learning.
Graph Filtration Learning
May 27, 2019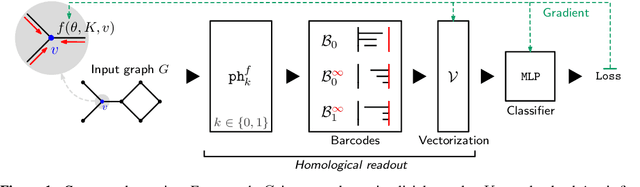
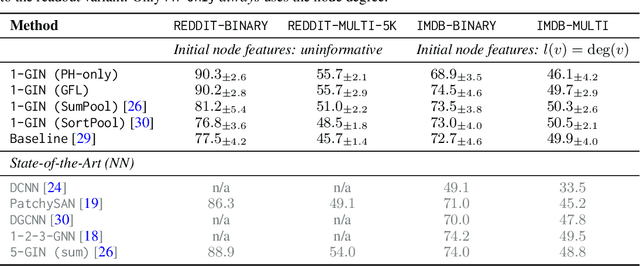


Abstract:We propose an approach to learning with graph-structured data in the problem domain of graph classification. In particular, we present a novel type of readout operation to aggregate node features into a graph-level representation. To this end, we leverage persistent homology computed via a real-valued, learnable, filter function. We establish the theoretical foundation for differentiating through the persistent homology computation. Empirically, we show that this type of readout operation compares favorably to previous techniques, especially when the graph connectivity structure is informative for the learning problem.
Deep Learning with Topological Signatures
Feb 16, 2018



Abstract:Inferring topological and geometrical information from data can offer an alternative perspective on machine learning problems. Methods from topological data analysis, e.g., persistent homology, enable us to obtain such information, typically in the form of summary representations of topological features. However, such topological signatures often come with an unusual structure (e.g., multisets of intervals) that is highly impractical for most machine learning techniques. While many strategies have been proposed to map these topological signatures into machine learning compatible representations, they suffer from being agnostic to the target learning task. In contrast, we propose a technique that enables us to input topological signatures to deep neural networks and learn a task-optimal representation during training. Our approach is realized as a novel input layer with favorable theoretical properties. Classification experiments on 2D object shapes and social network graphs demonstrate the versatility of the approach and, in case of the latter, we even outperform the state-of-the-art by a large margin.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge