Connectivity-Optimized Representation Learning via Persistent Homology
Paper and Code
Jun 21, 2019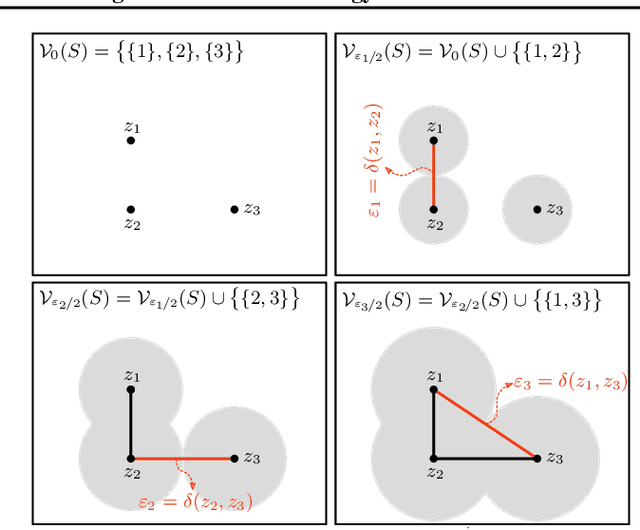
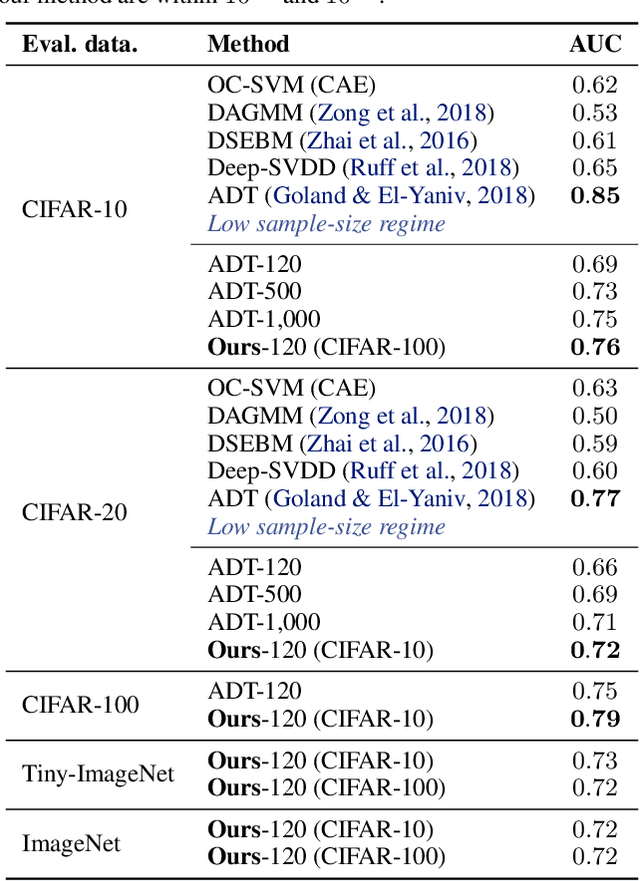
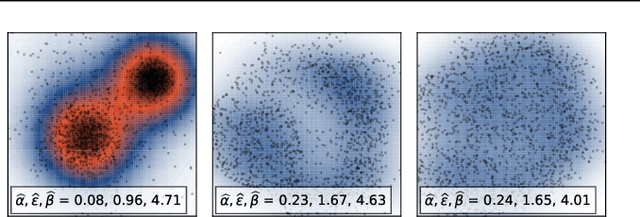
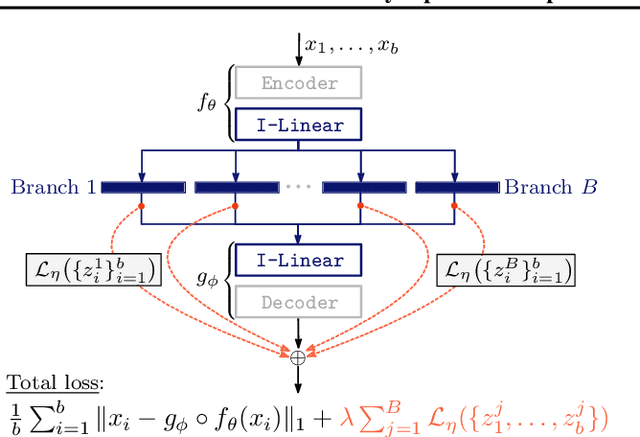
We study the problem of learning representations with controllable connectivity properties. This is beneficial in situations when the imposed structure can be leveraged upstream. In particular, we control the connectivity of an autoencoder's latent space via a novel type of loss, operating on information from persistent homology. Under mild conditions, this loss is differentiable and we present a theoretical analysis of the properties induced by the loss. We choose one-class learning as our upstream task and demonstrate that the imposed structure enables informed parameter selection for modeling the in-class distribution via kernel density estimators. Evaluated on computer vision data, these one-class models exhibit competitive performance and, in a low sample size regime, outperform other methods by a large margin. Notably, our results indicate that a single autoencoder, trained on auxiliary (unlabeled) data, yields a mapping into latent space that can be reused across datasets for one-class learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge