Model-agnostic variable importance for predictive uncertainty: an entropy-based approach

In order to trust the predictions of a machine learning algorithm, it is necessary to understand the factors that contribute to those predictions. In the case of probabilistic and uncertainty-aware models, it is necessary to understand not only the reasons for the predictions themselves, but also the model's level of confidence in those predictions. In this paper, we show how existing methods in explainability can be extended to uncertainty-aware models and how such extensions can be used to understand the sources of uncertainty in a model's predictive distribution. In particular, by adapting permutation feature importance, partial dependence plots, and individual conditional expectation plots, we demonstrate that novel insights into model behaviour may be obtained and that these methods can be used to measure the impact of features on both the entropy of the predictive distribution and the log-likelihood of the ground truth labels under that distribution. With experiments using both synthetic and real-world data, we demonstrate the utility of these approaches in understanding both the sources of uncertainty and their impact on model performance.

A max-affine spline approximation of neural networks using the Legendre transform of a convex-concave representation

This work presents a novel algorithm for transforming a neural network into a spline representation. Unlike previous work that required convex and piecewise-affine network operators to create a max-affine spline alternate form, this work relaxes this constraint. The only constraint is that the function be bounded and possess a well-define second derivative, although this was shown experimentally to not be strictly necessary. It can also be performed over the whole network rather than on each layer independently. As in previous work, this bridges the gap between neural networks and approximation theory but also enables the visualisation of network feature maps. Mathematical proof and experimental investigation of the technique is performed with approximation error and feature maps being extracted from a range of architectures, including convolutional neural networks.

A Unified Theory of Diversity in Ensemble Learning

We present a theory of ensemble diversity, explaining the nature and effect of diversity for a wide range of supervised learning scenarios. This challenge, of understanding ensemble diversity, has been referred to as the holy grail of ensemble learning, an open question for over 30 years. Our framework reveals that diversity is in fact a hidden dimension in the bias-variance decomposition of an ensemble. In particular, we prove a family of exact bias-variance-diversity decompositions, for both classification and regression losses, e.g., squared, and cross-entropy. The framework provides a methodology to automatically identify the combiner rule enabling such a decomposition, specific to the loss. The formulation of diversity is therefore dependent on just two design choices: the loss, and the combiner. For certain choices (e.g., 0-1 loss with majority voting) the effect of diversity is necessarily dependent on the target label. Experiments illustrate how we can use our framework to understand the diversity-encouraging mechanisms of popular ensemble methods: Bagging, Boosting, and Random Forests.

Bias-Variance Decompositions for Margin Losses

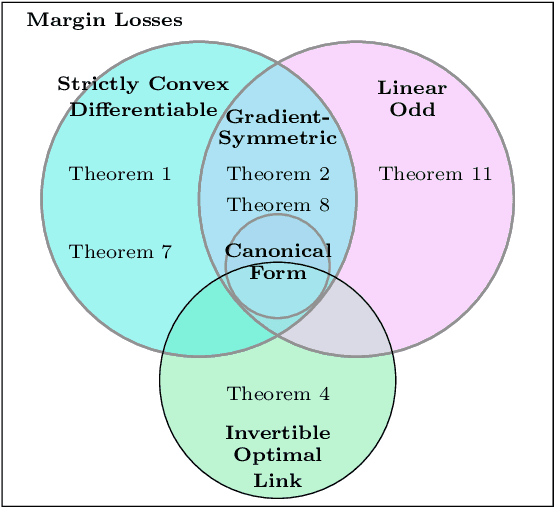
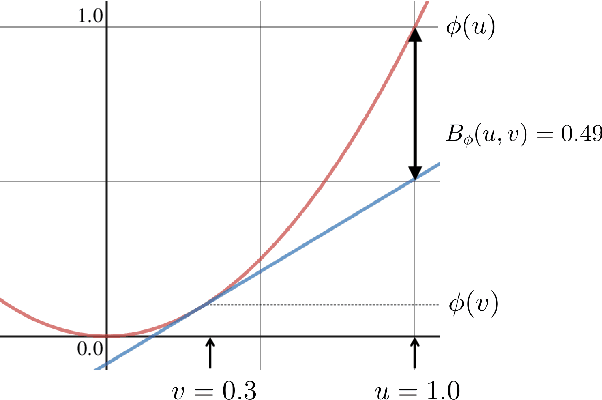
We introduce a novel bias-variance decomposition for a range of strictly convex margin losses, including the logistic loss (minimized by the classic LogitBoost algorithm), as well as the squared margin loss and canonical boosting loss. Furthermore, we show that, for all strictly convex margin losses, the expected risk decomposes into the risk of a "central" model and a term quantifying variation in the functional margin with respect to variations in the training data. These decompositions provide a diagnostic tool for practitioners to understand model overfitting/underfitting, and have implications for additive ensemble models -- for example, when our bias-variance decomposition holds, there is a corresponding "ambiguity" decomposition, which can be used to quantify model diversity.