A Unified Theory of Diversity in Ensemble Learning

We present a theory of ensemble diversity, explaining the nature and effect of diversity for a wide range of supervised learning scenarios. This challenge, of understanding ensemble diversity, has been referred to as the holy grail of ensemble learning, an open question for over 30 years. Our framework reveals that diversity is in fact a hidden dimension in the bias-variance decomposition of an ensemble. In particular, we prove a family of exact bias-variance-diversity decompositions, for both classification and regression losses, e.g., squared, and cross-entropy. The framework provides a methodology to automatically identify the combiner rule enabling such a decomposition, specific to the loss. The formulation of diversity is therefore dependent on just two design choices: the loss, and the combiner. For certain choices (e.g., 0-1 loss with majority voting) the effect of diversity is necessarily dependent on the target label. Experiments illustrate how we can use our framework to understand the diversity-encouraging mechanisms of popular ensemble methods: Bagging, Boosting, and Random Forests.

Margin Maximization as Lossless Maximal Compression

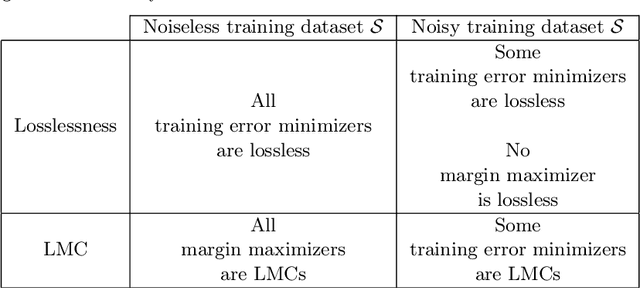
The ultimate goal of a supervised learning algorithm is to produce models constructed on the training data that can generalize well to new examples. In classification, functional margin maximization -- correctly classifying as many training examples as possible with maximal confidence --has been known to construct models with good generalization guarantees. This work gives an information-theoretic interpretation of a margin maximizing model on a noiseless training dataset as one that achieves lossless maximal compression of said dataset -- i.e. extracts from the features all the useful information for predicting the label and no more. The connection offers new insights on generalization in supervised machine learning, showing margin maximization as a special case (that of classification) of a more general principle and explains the success and potential limitations of popular learning algorithms like gradient boosting. We support our observations with theoretical arguments and empirical evidence and identify interesting directions for future work.

Joint Training of Neural Network Ensembles

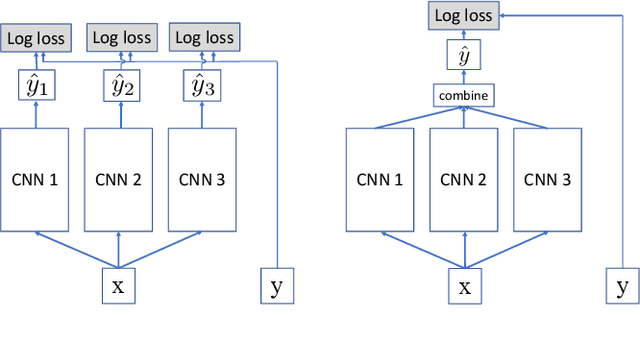
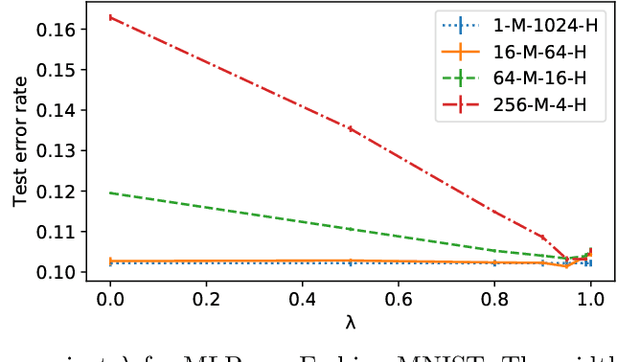
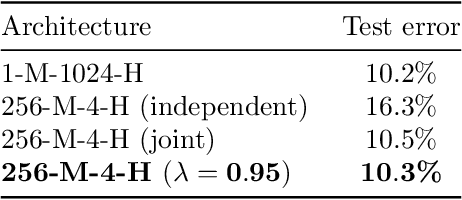
We examine the practice of joint training for neural network ensembles, in which a multi-branch architecture is trained via single loss. This approach has recently gained traction, with claims of greater accuracy per parameter along with increased parallelism. We introduce a family of novel loss functions generalizing multiple previously proposed approaches, with which we study theoretical and empirical properties of joint training. These losses interpolate smoothly between independent and joint training of predictors, demonstrating that joint training has several disadvantages not observed in prior work. However, with appropriate regularization via our proposed loss, the method shows new promise in resource limited scenarios and fault-tolerant systems, e.g., IoT and edge devices. Finally, we discuss how these results may have implications for general multi-branch architectures such as ResNeXt and Inception.