Bias-Variance Decompositions for Margin Losses
Paper and Code
Apr 26, 2022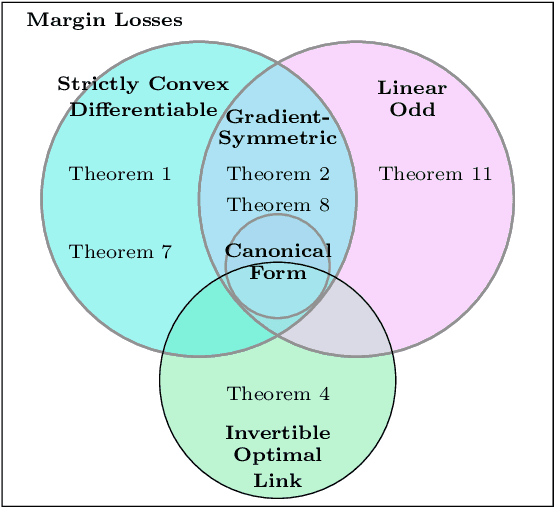


We introduce a novel bias-variance decomposition for a range of strictly convex margin losses, including the logistic loss (minimized by the classic LogitBoost algorithm), as well as the squared margin loss and canonical boosting loss. Furthermore, we show that, for all strictly convex margin losses, the expected risk decomposes into the risk of a "central" model and a term quantifying variation in the functional margin with respect to variations in the training data. These decompositions provide a diagnostic tool for practitioners to understand model overfitting/underfitting, and have implications for additive ensemble models -- for example, when our bias-variance decomposition holds, there is a corresponding "ambiguity" decomposition, which can be used to quantify model diversity.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge