Structural Conditions for Projection-Cost Preservation via Randomized Matrix Multiplication
Paper and Code
Aug 17, 2018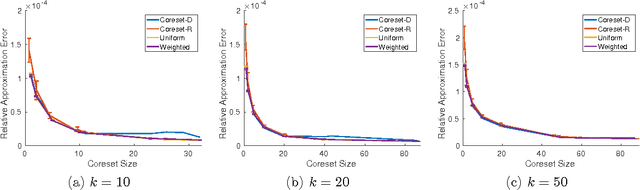
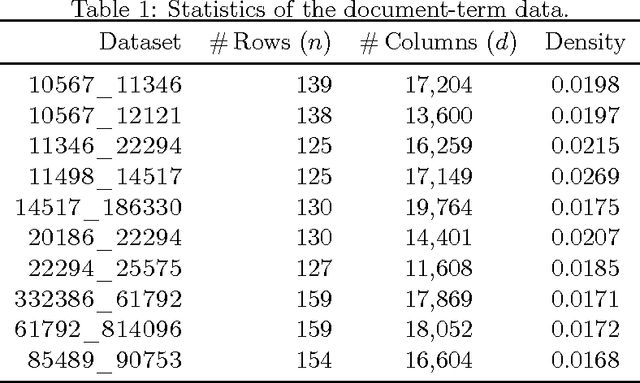


Projection-cost preservation is a low-rank approximation guarantee which ensures that the cost of any rank-$k$ projection can be preserved using a smaller sketch of the original data matrix. We present a general structural result outlining four sufficient conditions to achieve projection-cost preservation. These conditions can be satisfied using tools from the Randomized Linear Algebra literature.
* 16 pages
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge