Marconi: Prefix Caching for the Era of Hybrid LLMs

Hybrid models that combine the language modeling capabilities of Attention layers with the efficiency of Recurrent layers (e.g., State Space Models) have gained traction in practically supporting long contexts in Large Language Model serving. Yet, the unique properties of these models complicate the usage of complementary efficiency optimizations such as prefix caching that skip redundant computations across requests. Most notably, their use of in-place state updates for recurrent layers precludes rolling back cache entries for partial sequence overlaps, and instead mandates only exact-match cache hits; the effect is a deluge of (large) cache entries per sequence, most of which yield minimal reuse opportunities. We present Marconi, the first system that supports efficient prefix caching with Hybrid LLMs. Key to Marconi are its novel admission and eviction policies that more judiciously assess potential cache entries based not only on recency, but also on (1) forecasts of their reuse likelihood across a taxonomy of different hit scenarios, and (2) the compute savings that hits deliver relative to memory footprints. Across diverse workloads and Hybrid models, Marconi achieves up to 34.4$\times$ higher token hit rates (71.1% or 617 ms lower TTFT) compared to state-of-the-art prefix caching systems.

MADA: Meta-Adaptive Optimizers through hyper-gradient Descent

Since Adam was introduced, several novel adaptive optimizers for deep learning have been proposed. These optimizers typically excel in some tasks but may not outperform Adam uniformly across all tasks. In this work, we introduce Meta-Adaptive Optimizers (MADA), a unified optimizer framework that can generalize several known optimizers and dynamically learn the most suitable one during training. The key idea in MADA is to parameterize the space of optimizers and search through it using hyper-gradient descent. Numerical results suggest that MADA is robust against sub-optimally tuned hyper-parameters, and outperforms Adam, Lion, and Adan with their default hyper-parameters, often even with optimized hyper-parameters. We also propose AVGrad, a variant of AMSGrad where the maximum operator is replaced with averaging, and observe that it performs better within MADA. Finally, we provide a convergence analysis to show that interpolation of optimizers (specifically, AVGrad and Adam) can improve their error bounds (up to constants), hinting at an advantage for meta-optimizers.

Amazon SageMaker Model Parallelism: A General and Flexible Framework for Large Model Training

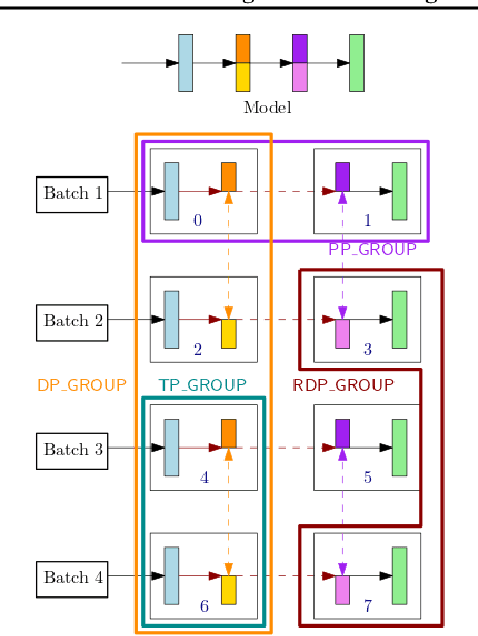
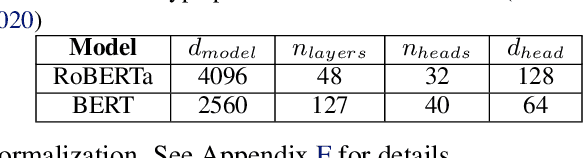
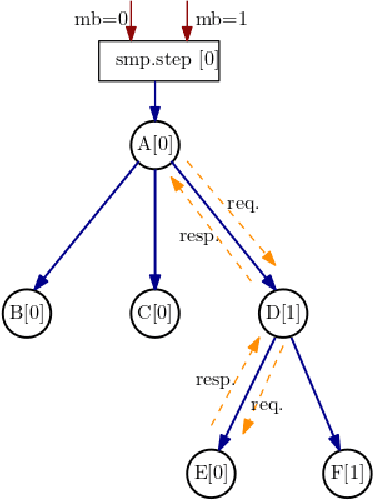
With deep learning models rapidly growing in size, systems-level solutions for large-model training are required. We present Amazon SageMaker model parallelism, a software library that integrates with PyTorch, and enables easy training of large models using model parallelism and other memory-saving features. In contrast to existing solutions, the implementation of the SageMaker library is much more generic and flexible, in that it can automatically partition and run pipeline parallelism over arbitrary model architectures with minimal code change, and also offers a general and extensible framework for tensor parallelism, which supports a wider range of use cases, and is modular enough to be easily applied to new training scripts. The library also preserves the native PyTorch user experience to a much larger degree, supporting module re-use and dynamic graphs, while giving the user full control over the details of the training step. We evaluate performance over GPT-3, RoBERTa, BERT, and neural collaborative filtering, and demonstrate competitive performance over existing solutions.

Qsparse-local-SGD: Distributed SGD with Quantization, Sparsification, and Local Computations

Communication bottleneck has been identified as a significant issue in distributed optimization of large-scale learning models. Recently, several approaches to mitigate this problem have been proposed, including different forms of gradient compression or computing local models and mixing them iteratively. In this paper we propose \emph{Qsparse-local-SGD} algorithm, which combines aggressive sparsification with quantization and local computation along with error compensation, by keeping track of the difference between the true and compressed gradients. We propose both synchronous and asynchronous implementations of \emph{Qsparse-local-SGD}. We analyze convergence for \emph{Qsparse-local-SGD} in the \emph{distributed} setting for smooth non-convex and convex objective functions. We demonstrate that \emph{Qsparse-local-SGD} converges at the same rate as vanilla distributed SGD for many important classes of sparsifiers and quantizers. We use \emph{Qsparse-local-SGD} to train ResNet-50 on ImageNet, and show that it results in significant savings over the state-of-the-art, in the number of bits transmitted to reach target accuracy.

Densifying Assumed-sparse Tensors: Improving Memory Efficiency and MPI Collective Performance during Tensor Accumulation for Parallelized Training of Neural Machine Translation Models

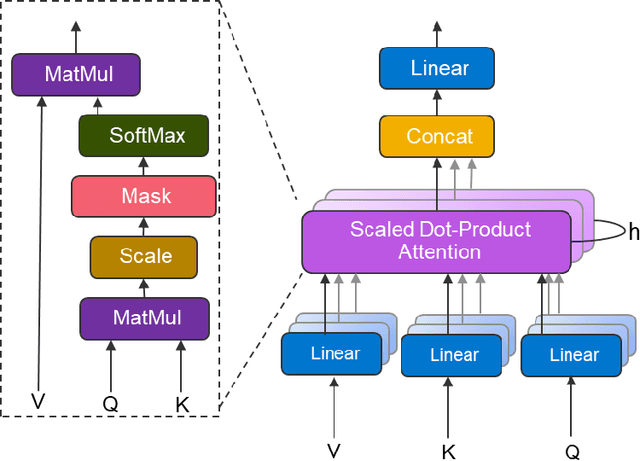
Neural machine translation - using neural networks to translate human language - is an area of active research exploring new neuron types and network topologies with the goal of dramatically improving machine translation performance. Current state-of-the-art approaches, such as the multi-head attention-based transformer, require very large translation corpuses and many epochs to produce models of reasonable quality. Recent attempts to parallelize the official TensorFlow "Transformer" model across multiple nodes have hit roadblocks due to excessive memory use and resulting out of memory errors when performing MPI collectives. This paper describes modifications made to the Horovod MPI-based distributed training framework to reduce memory usage for transformer models by converting assumed-sparse tensors to dense tensors, and subsequently replacing sparse gradient gather with dense gradient reduction. The result is a dramatic increase in scale-out capability, with CPU-only scaling tests achieving 91% weak scaling efficiency up to 1200 MPI processes (300 nodes), and up to 65% strong scaling efficiency up to 400 MPI processes (200 nodes) using the Stampede2 supercomputer.

Differentially Private Consensus-Based Distributed Optimization

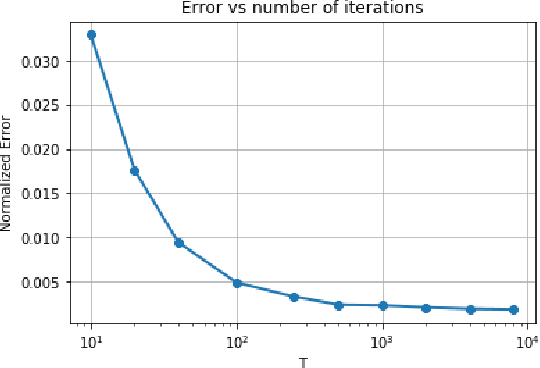
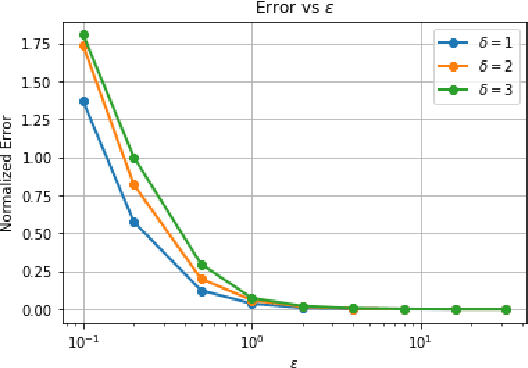
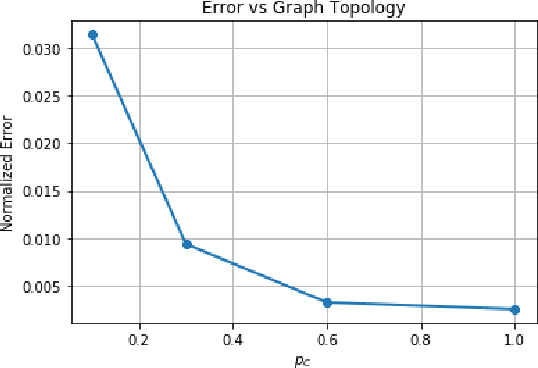
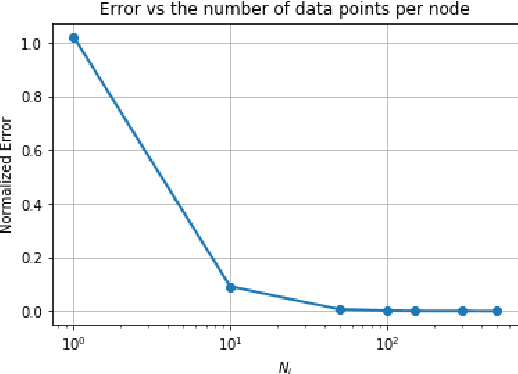
Data privacy is an important concern in learning, when datasets contain sensitive information about individuals. This paper considers consensus-based distributed optimization under data privacy constraints. Consensus-based optimization consists of a set of computational nodes arranged in a graph, each having a local objective that depends on their local data, where in every step nodes take a linear combination of their neighbors' messages, as well as taking a new gradient step. Since the algorithm requires exchanging messages that depend on local data, private information gets leaked at every step. Taking $(\epsilon, \delta)$-differential privacy (DP) as our criterion, we consider the strategy where the nodes add random noise to their messages before broadcasting it, and show that the method achieves convergence with a bounded mean-squared error, while satisfying $(\epsilon, \delta)$-DP. By relaxing the more stringent $\epsilon$-DP requirement in previous work, we strengthen a known convergence result in the literature. We conclude the paper with numerical results demonstrating the effectiveness of our methods for mean estimation.

Privacy-Utility Trade-off of Linear Regression under Random Projections and Additive Noise

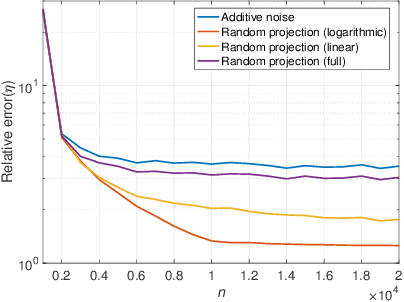
Data privacy is an important concern in machine learning, and is fundamentally at odds with the task of training useful learning models, which typically require the acquisition of large amounts of private user data. One possible way of fulfilling the machine learning task while preserving user privacy is to train the model on a transformed, noisy version of the data, which does not reveal the data itself directly to the training procedure. In this work, we analyze the privacy-utility trade-off of two such schemes for the problem of linear regression: additive noise, and random projections. In contrast to previous work, we consider a recently proposed notion of differential privacy that is based on conditional mutual information (MI-DP), which is stronger than the conventional $(\epsilon, \delta)$-differential privacy, and use relative objective error as the utility metric. We find that projecting the data to a lower-dimensional subspace before adding noise attains a better trade-off in general. We also make a connection between privacy problem and (non-coherent) SIMO, which has been extensively studied in wireless communication, and use tools from there for the analysis. We present numerical results demonstrating the performance of the schemes.

Redundancy Techniques for Straggler Mitigation in Distributed Optimization and Learning

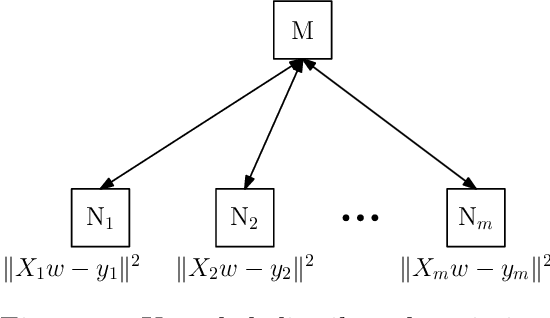
Performance of distributed optimization and learning systems is bottlenecked by "straggler" nodes and slow communication links, which significantly delay computation. We propose a distributed optimization framework where the dataset is "encoded" to have an over-complete representation with built-in redundancy, and the straggling nodes in the system are dynamically left out of the computation at every iteration, whose loss is compensated by the embedded redundancy. We show that oblivious application of several popular optimization algorithms on encoded data, including gradient descent, L-BFGS, proximal gradient under data parallelism, and coordinate descent under model parallelism, converge to either approximate or exact solutions of the original problem when stragglers are treated as erasures. These convergence results are deterministic, i.e., they establish sample path convergence for arbitrary sequences of delay patterns or distributions on the nodes, and are independent of the tail behavior of the delay distribution. We demonstrate that equiangular tight frames have desirable properties as encoding matrices, and propose efficient mechanisms for encoding large-scale data. We implement the proposed technique on Amazon EC2 clusters, and demonstrate its performance over several learning problems, including matrix factorization, LASSO, ridge regression and logistic regression, and compare the proposed method with uncoded, asynchronous, and data replication strategies.

Straggler Mitigation in Distributed Optimization Through Data Encoding

Slow running or straggler tasks can significantly reduce computation speed in distributed computation. Recently, coding-theory-inspired approaches have been applied to mitigate the effect of straggling, through embedding redundancy in certain linear computational steps of the optimization algorithm, thus completing the computation without waiting for the stragglers. In this paper, we propose an alternate approach where we embed the redundancy directly in the data itself, and allow the computation to proceed completely oblivious to encoding. We propose several encoding schemes, and demonstrate that popular batch algorithms, such as gradient descent and L-BFGS, applied in a coding-oblivious manner, deterministically achieve sample path linear convergence to an approximate solution of the original problem, using an arbitrarily varying subset of the nodes at each iteration. Moreover, this approximation can be controlled by the amount of redundancy and the number of nodes used in each iteration. We provide experimental results demonstrating the advantage of the approach over uncoded and data replication strategies.