A Generative Framework for Personalized Learning and Estimation: Theory, Algorithms, and Privacy

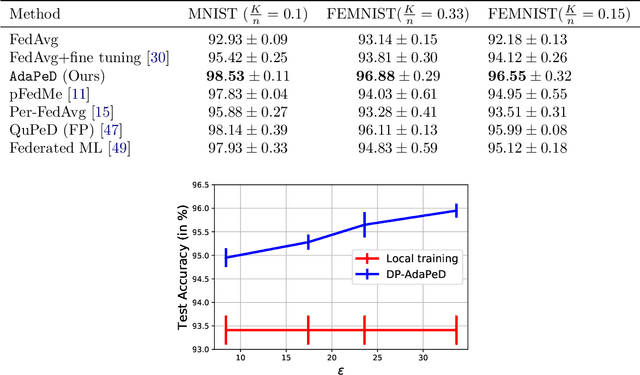
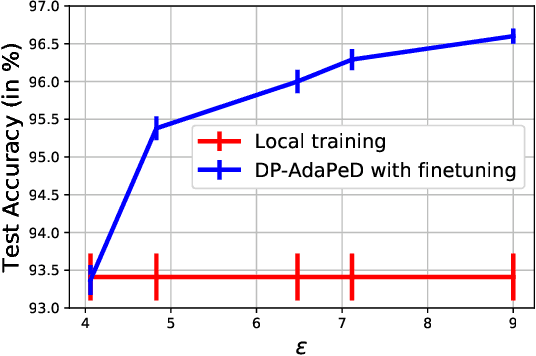
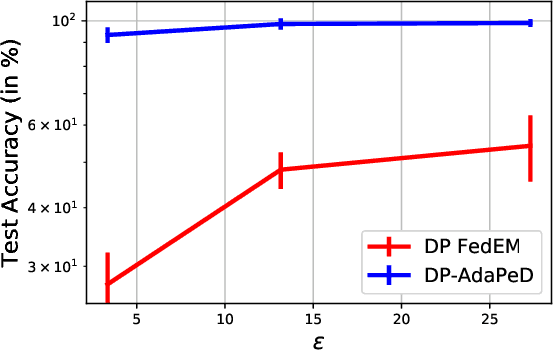
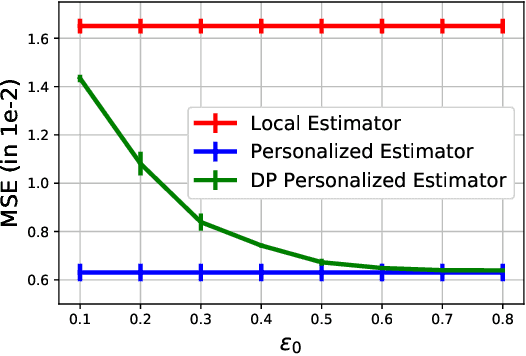
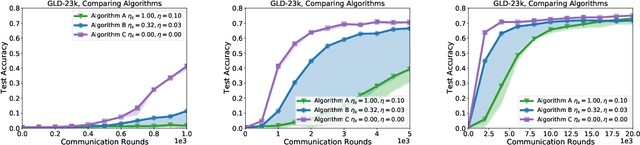
A distinguishing characteristic of federated learning is that the (local) client data could have statistical heterogeneity. This heterogeneity has motivated the design of personalized learning, where individual (personalized) models are trained, through collaboration. There have been various personalization methods proposed in literature, with seemingly very different forms and methods ranging from use of a single global model for local regularization and model interpolation, to use of multiple global models for personalized clustering, etc. In this work, we begin with a generative framework that could potentially unify several different algorithms as well as suggest new algorithms. We apply our generative framework to personalized estimation, and connect it to the classical empirical Bayes' methodology. We develop private personalized estimation under this framework. We then use our generative framework for learning, which unifies several known personalized FL algorithms and also suggests new ones; we propose and study a new algorithm AdaPeD based on a Knowledge Distillation, which numerically outperforms several known algorithms. We also develop privacy for personalized learning methods with guarantees for user-level privacy and composition. We numerically evaluate the performance as well as the privacy for both the estimation and learning problems, demonstrating the advantages of our proposed methods.

QuPeD: Quantized Personalization via Distillation with Applications to Federated Learning

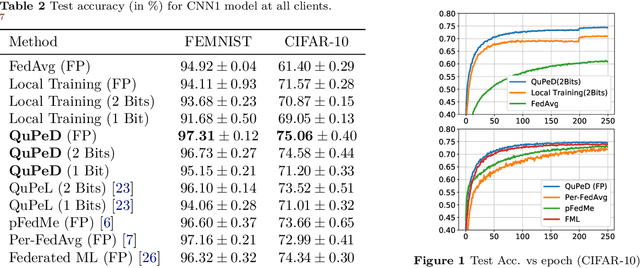
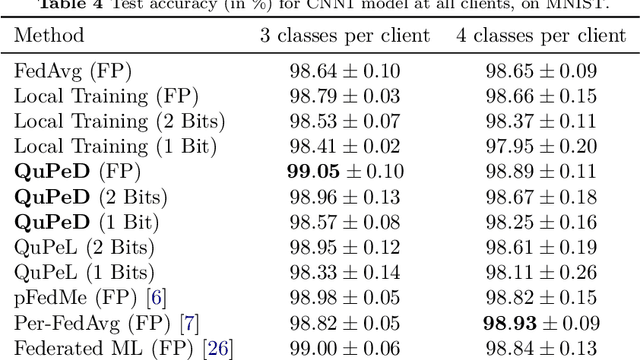
Traditionally, federated learning (FL) aims to train a single global model while collaboratively using multiple clients and a server. Two natural challenges that FL algorithms face are heterogeneity in data across clients and collaboration of clients with {\em diverse resources}. In this work, we introduce a \textit{quantized} and \textit{personalized} FL algorithm QuPeD that facilitates collective (personalized model compression) training via \textit{knowledge distillation} (KD) among clients who have access to heterogeneous data and resources. For personalization, we allow clients to learn \textit{compressed personalized models} with different quantization parameters and model dimensions/structures. Towards this, first we propose an algorithm for learning quantized models through a relaxed optimization problem, where quantization values are also optimized over. When each client participating in the (federated) learning process has different requirements for the compressed model (both in model dimension and precision), we formulate a compressed personalization framework by introducing knowledge distillation loss for local client objectives collaborating through a global model. We develop an alternating proximal gradient update for solving this compressed personalization problem, and analyze its convergence properties. Numerically, we validate that QuPeD outperforms competing personalized FL methods, FedAvg, and local training of clients in various heterogeneous settings.

Renyi Differential Privacy of the Subsampled Shuffle Model in Distributed Learning

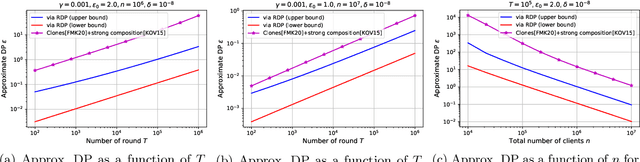
We study privacy in a distributed learning framework, where clients collaboratively build a learning model iteratively through interactions with a server from whom we need privacy. Motivated by stochastic optimization and the federated learning (FL) paradigm, we focus on the case where a small fraction of data samples are randomly sub-sampled in each round to participate in the learning process, which also enables privacy amplification. To obtain even stronger local privacy guarantees, we study this in the shuffle privacy model, where each client randomizes its response using a local differentially private (LDP) mechanism and the server only receives a random permutation (shuffle) of the clients' responses without their association to each client. The principal result of this paper is a privacy-optimization performance trade-off for discrete randomization mechanisms in this sub-sampled shuffle privacy model. This is enabled through a new theoretical technique to analyze the Renyi Differential Privacy (RDP) of the sub-sampled shuffle model. We numerically demonstrate that, for important regimes, with composition our bound yields significant improvement in privacy guarantee over the state-of-the-art approximate Differential Privacy (DP) guarantee (with strong composition) for sub-sampled shuffled models. We also demonstrate numerically significant improvement in privacy-learning performance operating point using real data sets.

A Field Guide to Federated Optimization

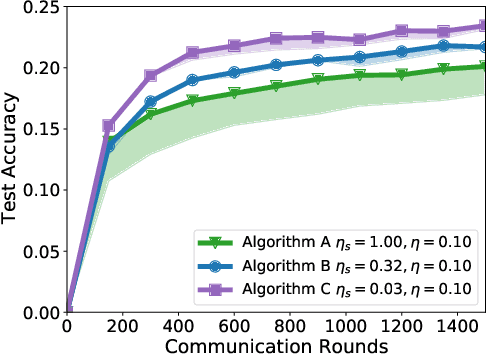
Federated learning and analytics are a distributed approach for collaboratively learning models (or statistics) from decentralized data, motivated by and designed for privacy protection. The distributed learning process can be formulated as solving federated optimization problems, which emphasize communication efficiency, data heterogeneity, compatibility with privacy and system requirements, and other constraints that are not primary considerations in other problem settings. This paper provides recommendations and guidelines on formulating, designing, evaluating and analyzing federated optimization algorithms through concrete examples and practical implementation, with a focus on conducting effective simulations to infer real-world performance. The goal of this work is not to survey the current literature, but to inspire researchers and practitioners to design federated learning algorithms that can be used in various practical applications.

On the Renyi Differential Privacy of the Shuffle Model

The central question studied in this paper is Renyi Differential Privacy (RDP) guarantees for general discrete local mechanisms in the shuffle privacy model. In the shuffle model, each of the $n$ clients randomizes its response using a local differentially private (LDP) mechanism and the untrusted server only receives a random permutation (shuffle) of the client responses without association to each client. The principal result in this paper is the first non-trivial RDP guarantee for general discrete local randomization mechanisms in the shuffled privacy model, and we develop new analysis techniques for deriving our results which could be of independent interest. In applications, such an RDP guarantee is most useful when we use it for composing several private interactions. We numerically demonstrate that, for important regimes, with composition our bound yields an improvement in privacy guarantee by a factor of $8\times$ over the state-of-the-art approximate Differential Privacy (DP) guarantee (with standard composition) for shuffled models. Moreover, combining with Poisson subsampling, our result leads to at least $10\times$ improvement over subsampled approximate DP with standard composition.

QuPeL: Quantized Personalization with Applications to Federated Learning

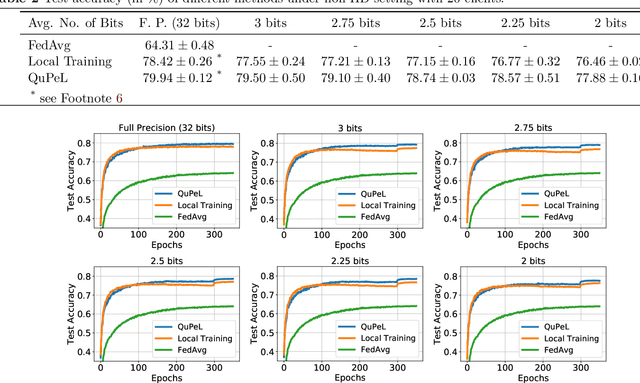
Traditionally, federated learning (FL) aims to train a single global model while collaboratively using multiple clients and a server. Two natural challenges that FL algorithms face are heterogeneity in data across clients and collaboration of clients with {\em diverse resources}. In this work, we introduce a \textit{quantized} and \textit{personalized} FL algorithm QuPeL that facilitates collective training with heterogeneous clients while respecting resource diversity. For personalization, we allow clients to learn \textit{compressed personalized models} with different quantization parameters depending on their resources. Towards this, first we propose an algorithm for learning quantized models through a relaxed optimization problem, where quantization values are also optimized over. When each client participating in the (federated) learning process has different requirements of the quantized model (both in value and precision), we formulate a quantized personalization framework by introducing a penalty term for local client objectives against a globally trained model to encourage collaboration. We develop an alternating proximal gradient update for solving this quantized personalization problem, and we analyze its convergence properties. Numerically, we show that optimizing over the quantization levels increases the performance and we validate that QuPeL outperforms both FedAvg and local training of clients in a heterogeneous setting.

Shuffled Model of Federated Learning: Privacy, Communication and Accuracy Trade-offs

We consider a distributed empirical risk minimization (ERM) optimization problem with communication efficiency and privacy requirements, motivated by the federated learning (FL) framework. Unique challenges to the traditional ERM problem in the context of FL include (i) need to provide privacy guarantees on clients' data, (ii) compress the communication between clients and the server, since clients might have low-bandwidth links, (iii) work with a dynamic client population at each round of communication between the server and the clients, as a small fraction of clients are sampled at each round. To address these challenges we develop (optimal) communication-efficient schemes for private mean estimation for several $\ell_p$ spaces, enabling efficient gradient aggregation for each iteration of the optimization solution of the ERM. We also provide lower and upper bounds for mean estimation with privacy and communication constraints for arbitrary $\ell_p$ spaces. To get the overall communication, privacy, and optimization performance operation point, we combine this with privacy amplification opportunities inherent to this setup. Our solution takes advantage of the inherent privacy amplification provided by client sampling and data sampling at each client (through Stochastic Gradient Descent) as well as the recently developed privacy framework using anonymization, which effectively presents to the server responses that are randomly shuffled with respect to the clients. Putting these together, we demonstrate that one can get the same privacy, optimization-performance operating point developed in recent methods that use full-precision communication, but at a much lower communication cost, i.e., effectively getting communication efficiency for "free".

Byzantine-Resilient High-Dimensional SGD with Local Iterations on Heterogeneous Data

We study stochastic gradient descent (SGD) with local iterations in the presence of malicious/Byzantine clients, motivated by the federated learning. The clients, instead of communicating with the central server in every iteration, maintain their local models, which they update by taking several SGD iterations based on their own datasets and then communicate the net update with the server, thereby achieving communication-efficiency. Furthermore, only a subset of clients communicate with the server, and this subset may be different at different synchronization times. The Byzantine clients may collaborate and send arbitrary vectors to the server to disrupt the learning process. To combat the adversary, we employ an efficient high-dimensional robust mean estimation algorithm at the server to filter-out corrupt vectors; and to analyze the outlier-filtering procedure, we develop a novel matrix concentration result that may be of independent interest. We provide convergence analyses for both strongly-convex and non-convex smooth objectives in the heterogeneous data setting, where different clients may have different local datasets, and we do not make any probabilistic assumptions on data generation. We believe that ours is the first Byzantine-resilient algorithm and analysis with local iterations. We derive our convergence results under minimal assumptions of bounded variance for SGD and bounded gradient dissimilarity (which captures heterogeneity among local datasets); and we provide bounds on these quantities in the statistical heterogeneous data setting. We also extend our results to the case when clients compute full-batch gradients.

Successive Refinement of Privacy

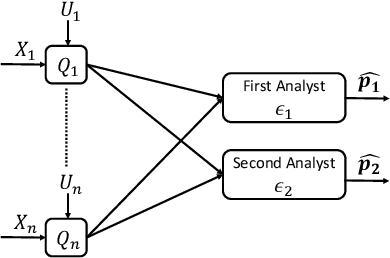
This work examines a novel question: how much randomness is needed to achieve local differential privacy (LDP)? A motivating scenario is providing {\em multiple levels of privacy} to multiple analysts, either for distribution or for heavy-hitter estimation, using the \emph{same} (randomized) output. We call this setting \emph{successive refinement of privacy}, as it provides hierarchical access to the raw data with different privacy levels. For example, the same randomized output could enable one analyst to reconstruct the input, while another can only estimate the distribution subject to LDP requirements. This extends the classical Shannon (wiretap) security setting to local differential privacy. We provide (order-wise) tight characterizations of privacy-utility-randomness trade-offs in several cases for distribution estimation, including the standard LDP setting under a randomness constraint. We also provide a non-trivial privacy mechanism for multi-level privacy. Furthermore, we show that we cannot reuse random keys over time while preserving privacy of each user.

Byzantine-Resilient SGD in High Dimensions on Heterogeneous Data

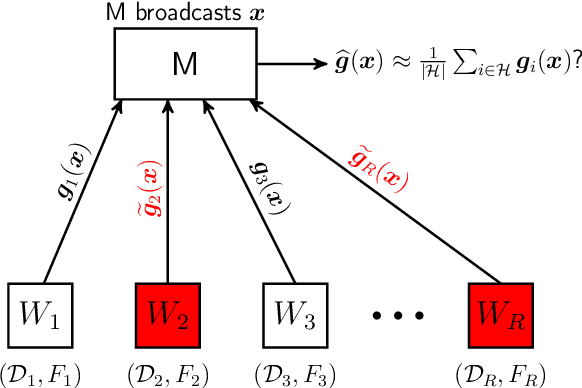
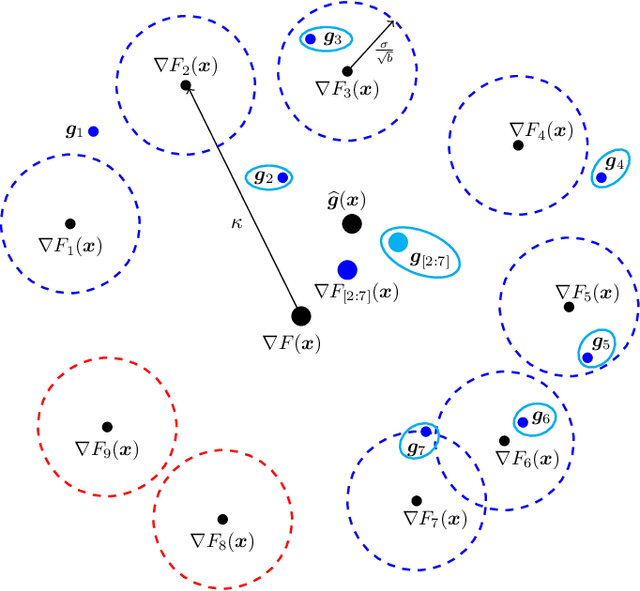
We study distributed stochastic gradient descent (SGD) in the master-worker architecture under Byzantine attacks. We consider the heterogeneous data model, where different workers may have different local datasets, and we do not make any probabilistic assumptions on data generation. At the core of our algorithm, we use the polynomial-time outlier-filtering procedure for robust mean estimation proposed by Steinhardt et al. (ITCS 2018) to filter-out corrupt gradients. In order to be able to apply their filtering procedure in our {\em heterogeneous} data setting where workers compute {\em stochastic} gradients, we derive a new matrix concentration result, which may be of independent interest. We provide convergence analyses for smooth strongly-convex and non-convex objectives. We derive our results under the bounded variance assumption on local stochastic gradients and a {\em deterministic} condition on datasets, namely, gradient dissimilarity; and for both these quantities, we provide concrete bounds in the statistical heterogeneous data model. We give a trade-off between the mini-batch size for stochastic gradients and the approximation error. Our algorithm can tolerate up to $\frac{1}{4}$ fraction Byzantine workers. It can find approximate optimal parameters in the strongly-convex setting exponentially fast and reach to an approximate stationary point in the non-convex setting with a linear speed, thus, matching the convergence rates of vanilla SGD in the Byzantine-free setting. We also propose and analyze a Byzantine-resilient SGD algorithm with gradient compression, where workers send $k$ random coordinates of their gradients. Under mild conditions, we show a $\frac{d}{k}$-factor saving in communication bits as well as decoding complexity over our compression-free algorithm without affecting its convergence rate (order-wise) and the approximation error.