Antonious M. Girgis
Learning from straggler clients in federated learning
Mar 14, 2024



Abstract:How well do existing federated learning algorithms learn from client devices that return model updates with a significant time delay? Is it even possible to learn effectively from clients that report back minutes, hours, or days after being scheduled? We answer these questions by developing Monte Carlo simulations of client latency that are guided by real-world applications. We study synchronous optimization algorithms like FedAvg and FedAdam as well as the asynchronous FedBuff algorithm, and observe that all these existing approaches struggle to learn from severely delayed clients. To improve upon this situation, we experiment with modifications, including distillation regularization and exponential moving averages of model weights. Finally, we introduce two new algorithms, FARe-DUST and FeAST-on-MSG, based on distillation and averaging, respectively. Experiments with the EMNIST, CIFAR-100, and StackOverflow benchmark federated learning tasks demonstrate that our new algorithms outperform existing ones in terms of accuracy for straggler clients, while also providing better trade-offs between training time and total accuracy.
Multi-Message Shuffled Privacy in Federated Learning
Feb 22, 2023Abstract:We study differentially private distributed optimization under communication constraints. A server using SGD for optimization aggregates the client-side local gradients for model updates using distributed mean estimation (DME). We develop a communication-efficient private DME, using the recently developed multi-message shuffled (MMS) privacy framework. We analyze our proposed DME scheme to show that it achieves the order-optimal privacy-communication-performance tradeoff resolving an open question in [1], whether the shuffled models can improve the tradeoff obtained in Secure Aggregation. This also resolves an open question on the optimal trade-off for private vector sum in the MMS model. We achieve it through a novel privacy mechanism that non-uniformly allocates privacy at different resolutions of the local gradient vectors. These results are directly applied to give guarantees on private distributed learning algorithms using this for private gradient aggregation iteratively. We also numerically evaluate the private DME algorithms.
Differentially Private Stochastic Linear Bandits: (Almost) for Free
Jul 07, 2022
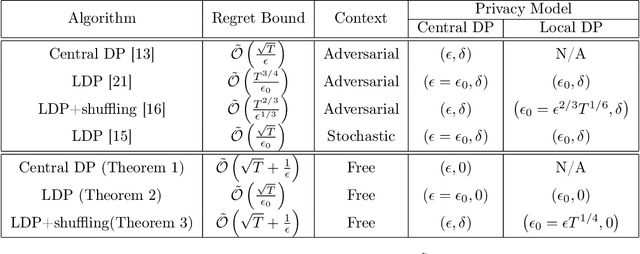
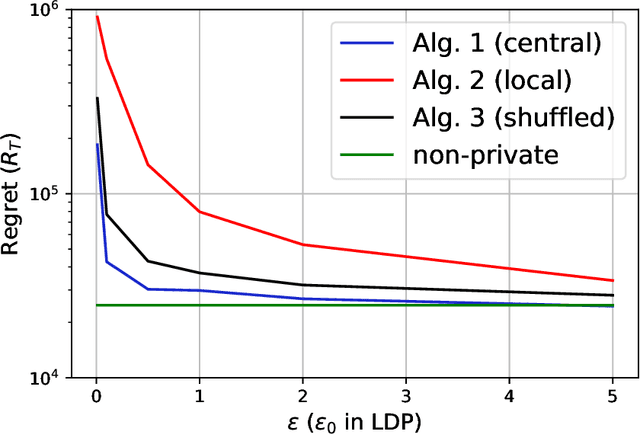

Abstract:In this paper, we propose differentially private algorithms for the problem of stochastic linear bandits in the central, local and shuffled models. In the central model, we achieve almost the same regret as the optimal non-private algorithms, which means we get privacy for free. In particular, we achieve a regret of $\tilde{O}(\sqrt{T}+\frac{1}{\epsilon})$ matching the known lower bound for private linear bandits, while the best previously known algorithm achieves $\tilde{O}(\frac{1}{\epsilon}\sqrt{T})$. In the local case, we achieve a regret of $\tilde{O}(\frac{1}{\epsilon}{\sqrt{T}})$ which matches the non-private regret for constant $\epsilon$, but suffers a regret penalty when $\epsilon$ is small. In the shuffled model, we also achieve regret of $\tilde{O}(\sqrt{T}+\frac{1}{\epsilon})$ %for small $\epsilon$ as in the central case, while the best previously known algorithm suffers a regret of $\tilde{O}(\frac{1}{\epsilon}{T^{3/5}})$. Our numerical evaluation validates our theoretical results.
A Generative Framework for Personalized Learning and Estimation: Theory, Algorithms, and Privacy
Jul 05, 2022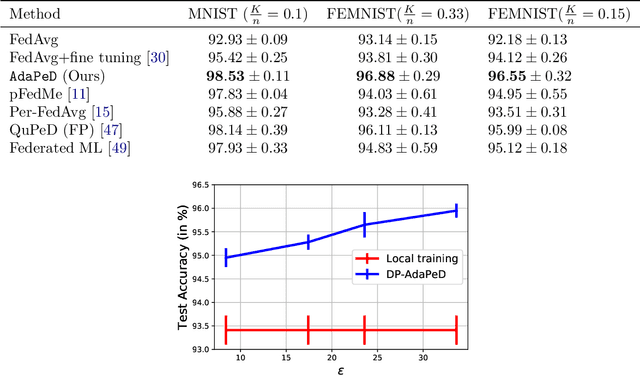
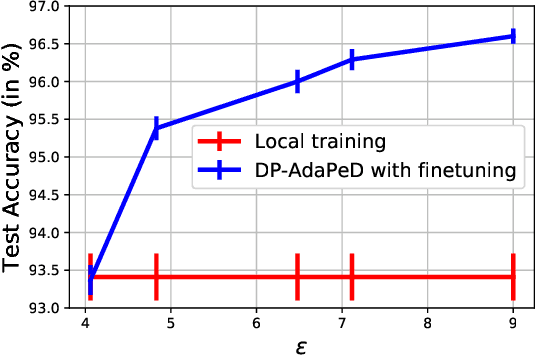
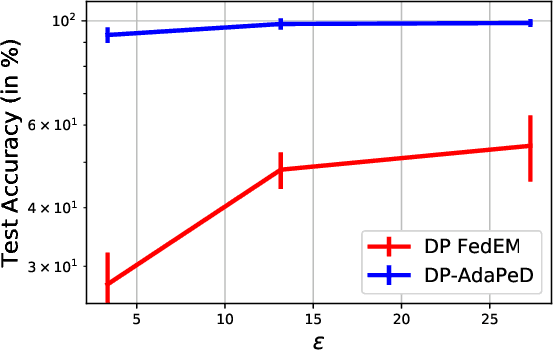
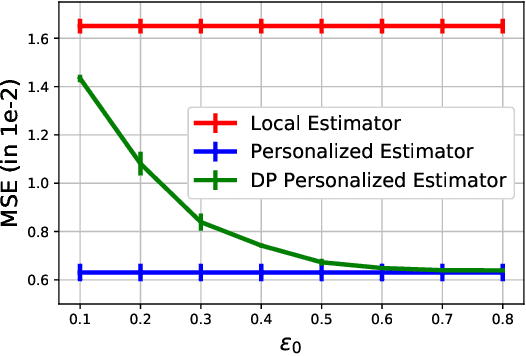
Abstract:A distinguishing characteristic of federated learning is that the (local) client data could have statistical heterogeneity. This heterogeneity has motivated the design of personalized learning, where individual (personalized) models are trained, through collaboration. There have been various personalization methods proposed in literature, with seemingly very different forms and methods ranging from use of a single global model for local regularization and model interpolation, to use of multiple global models for personalized clustering, etc. In this work, we begin with a generative framework that could potentially unify several different algorithms as well as suggest new algorithms. We apply our generative framework to personalized estimation, and connect it to the classical empirical Bayes' methodology. We develop private personalized estimation under this framework. We then use our generative framework for learning, which unifies several known personalized FL algorithms and also suggests new ones; we propose and study a new algorithm AdaPeD based on a Knowledge Distillation, which numerically outperforms several known algorithms. We also develop privacy for personalized learning methods with guarantees for user-level privacy and composition. We numerically evaluate the performance as well as the privacy for both the estimation and learning problems, demonstrating the advantages of our proposed methods.
Renyi Differential Privacy of the Subsampled Shuffle Model in Distributed Learning
Jul 19, 2021

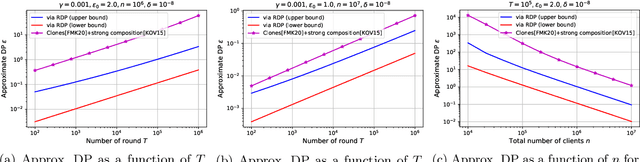

Abstract:We study privacy in a distributed learning framework, where clients collaboratively build a learning model iteratively through interactions with a server from whom we need privacy. Motivated by stochastic optimization and the federated learning (FL) paradigm, we focus on the case where a small fraction of data samples are randomly sub-sampled in each round to participate in the learning process, which also enables privacy amplification. To obtain even stronger local privacy guarantees, we study this in the shuffle privacy model, where each client randomizes its response using a local differentially private (LDP) mechanism and the server only receives a random permutation (shuffle) of the clients' responses without their association to each client. The principal result of this paper is a privacy-optimization performance trade-off for discrete randomization mechanisms in this sub-sampled shuffle privacy model. This is enabled through a new theoretical technique to analyze the Renyi Differential Privacy (RDP) of the sub-sampled shuffle model. We numerically demonstrate that, for important regimes, with composition our bound yields significant improvement in privacy guarantee over the state-of-the-art approximate Differential Privacy (DP) guarantee (with strong composition) for sub-sampled shuffled models. We also demonstrate numerically significant improvement in privacy-learning performance operating point using real data sets.
A Field Guide to Federated Optimization
Jul 14, 2021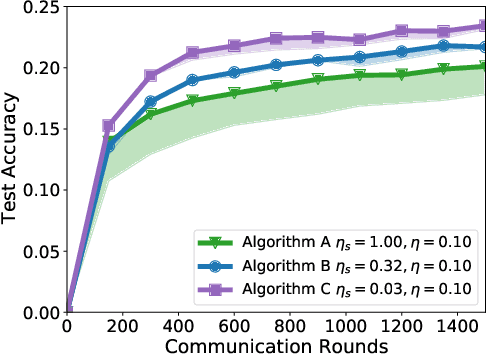


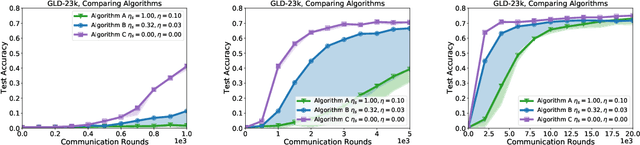
Abstract:Federated learning and analytics are a distributed approach for collaboratively learning models (or statistics) from decentralized data, motivated by and designed for privacy protection. The distributed learning process can be formulated as solving federated optimization problems, which emphasize communication efficiency, data heterogeneity, compatibility with privacy and system requirements, and other constraints that are not primary considerations in other problem settings. This paper provides recommendations and guidelines on formulating, designing, evaluating and analyzing federated optimization algorithms through concrete examples and practical implementation, with a focus on conducting effective simulations to infer real-world performance. The goal of this work is not to survey the current literature, but to inspire researchers and practitioners to design federated learning algorithms that can be used in various practical applications.
On the Renyi Differential Privacy of the Shuffle Model
May 11, 2021



Abstract:The central question studied in this paper is Renyi Differential Privacy (RDP) guarantees for general discrete local mechanisms in the shuffle privacy model. In the shuffle model, each of the $n$ clients randomizes its response using a local differentially private (LDP) mechanism and the untrusted server only receives a random permutation (shuffle) of the client responses without association to each client. The principal result in this paper is the first non-trivial RDP guarantee for general discrete local randomization mechanisms in the shuffled privacy model, and we develop new analysis techniques for deriving our results which could be of independent interest. In applications, such an RDP guarantee is most useful when we use it for composing several private interactions. We numerically demonstrate that, for important regimes, with composition our bound yields an improvement in privacy guarantee by a factor of $8\times$ over the state-of-the-art approximate Differential Privacy (DP) guarantee (with standard composition) for shuffled models. Moreover, combining with Poisson subsampling, our result leads to at least $10\times$ improvement over subsampled approximate DP with standard composition.
Shuffled Model of Federated Learning: Privacy, Communication and Accuracy Trade-offs
Aug 17, 2020
Abstract:We consider a distributed empirical risk minimization (ERM) optimization problem with communication efficiency and privacy requirements, motivated by the federated learning (FL) framework. Unique challenges to the traditional ERM problem in the context of FL include (i) need to provide privacy guarantees on clients' data, (ii) compress the communication between clients and the server, since clients might have low-bandwidth links, (iii) work with a dynamic client population at each round of communication between the server and the clients, as a small fraction of clients are sampled at each round. To address these challenges we develop (optimal) communication-efficient schemes for private mean estimation for several $\ell_p$ spaces, enabling efficient gradient aggregation for each iteration of the optimization solution of the ERM. We also provide lower and upper bounds for mean estimation with privacy and communication constraints for arbitrary $\ell_p$ spaces. To get the overall communication, privacy, and optimization performance operation point, we combine this with privacy amplification opportunities inherent to this setup. Our solution takes advantage of the inherent privacy amplification provided by client sampling and data sampling at each client (through Stochastic Gradient Descent) as well as the recently developed privacy framework using anonymization, which effectively presents to the server responses that are randomly shuffled with respect to the clients. Putting these together, we demonstrate that one can get the same privacy, optimization-performance operating point developed in recent methods that use full-precision communication, but at a much lower communication cost, i.e., effectively getting communication efficiency for "free".
Successive Refinement of Privacy
May 24, 2020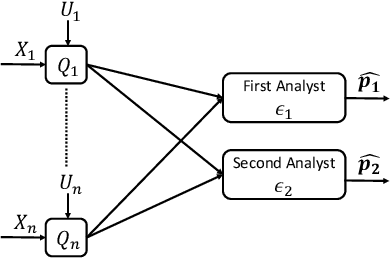



Abstract:This work examines a novel question: how much randomness is needed to achieve local differential privacy (LDP)? A motivating scenario is providing {\em multiple levels of privacy} to multiple analysts, either for distribution or for heavy-hitter estimation, using the \emph{same} (randomized) output. We call this setting \emph{successive refinement of privacy}, as it provides hierarchical access to the raw data with different privacy levels. For example, the same randomized output could enable one analyst to reconstruct the input, while another can only estimate the distribution subject to LDP requirements. This extends the classical Shannon (wiretap) security setting to local differential privacy. We provide (order-wise) tight characterizations of privacy-utility-randomness trade-offs in several cases for distribution estimation, including the standard LDP setting under a randomness constraint. We also provide a non-trivial privacy mechanism for multi-level privacy. Furthermore, we show that we cannot reuse random keys over time while preserving privacy of each user.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge