Renyi Differential Privacy of the Subsampled Shuffle Model in Distributed Learning
Paper and Code
Jul 19, 2021

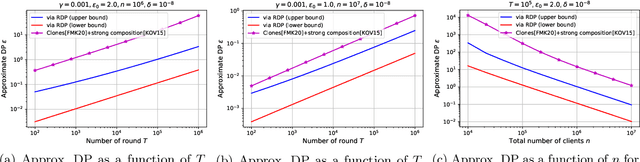

We study privacy in a distributed learning framework, where clients collaboratively build a learning model iteratively through interactions with a server from whom we need privacy. Motivated by stochastic optimization and the federated learning (FL) paradigm, we focus on the case where a small fraction of data samples are randomly sub-sampled in each round to participate in the learning process, which also enables privacy amplification. To obtain even stronger local privacy guarantees, we study this in the shuffle privacy model, where each client randomizes its response using a local differentially private (LDP) mechanism and the server only receives a random permutation (shuffle) of the clients' responses without their association to each client. The principal result of this paper is a privacy-optimization performance trade-off for discrete randomization mechanisms in this sub-sampled shuffle privacy model. This is enabled through a new theoretical technique to analyze the Renyi Differential Privacy (RDP) of the sub-sampled shuffle model. We numerically demonstrate that, for important regimes, with composition our bound yields significant improvement in privacy guarantee over the state-of-the-art approximate Differential Privacy (DP) guarantee (with strong composition) for sub-sampled shuffled models. We also demonstrate numerically significant improvement in privacy-learning performance operating point using real data sets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge