ICQuant: Index Coding enables Low-bit LLM Quantization

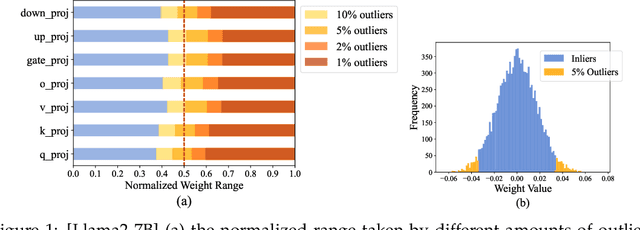
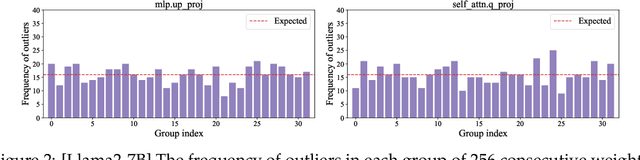
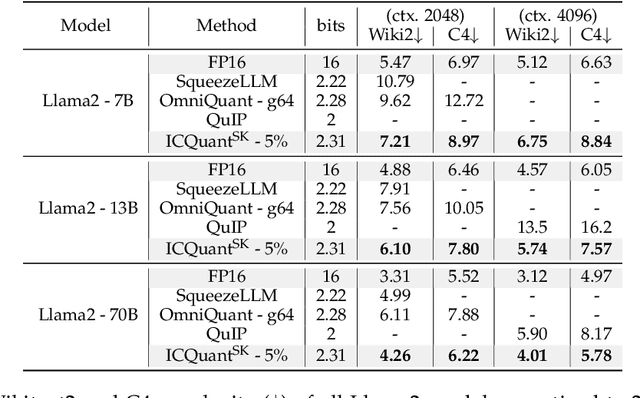
The rapid deployment of Large Language Models (LLMs) highlights the need for efficient low-bit post-training quantization (PTQ), due to their high memory costs. A key challenge in weight quantization is the presence of outliers, which inflate quantization ranges and lead to large errors. While a number of outlier suppression techniques have been proposed, they either: fail to effectively shrink the quantization range, or incur (relatively) high bit overhead. In this paper, we present ICQuant, a novel framework that leverages outlier statistics to design an efficient index coding scheme for outlier-aware weight-only quantization. Compared to existing outlier suppression techniques requiring $\approx 1$ bit overhead to halve the quantization range, ICQuant requires only $\approx 0.3$ bits; a significant saving in extreme compression regimes (e.g., 2-3 bits per weight). ICQuant can be used on top of any existing quantizers to eliminate outliers, improving the quantization quality. Using just 2.3 bits per weight and simple scalar quantizers, ICQuant improves the zero-shot accuracy of the 2-bit Llama3-70B model by up to 130% and 150% relative to QTIP and QuIP#; and it achieves comparable performance to the best-known fine-tuned quantizer (PV-tuning) without fine-tuning.

Does Feedback Help in Bandits with Arm Erasures?

We study a distributed multi-armed bandit (MAB) problem over arm erasure channels, motivated by the increasing adoption of MAB algorithms over communication-constrained networks. In this setup, the learner communicates the chosen arm to play to an agent over an erasure channel with probability $\epsilon \in [0,1)$; if an erasure occurs, the agent continues pulling the last successfully received arm; the learner always observes the reward of the arm pulled. In past work, we considered the case where the agent cannot convey feedback to the learner, and thus the learner does not know whether the arm played is the requested or the last successfully received one. In this paper, we instead consider the case where the agent can send feedback to the learner on whether the arm request was received, and thus the learner exactly knows which arm was played. Surprisingly, we prove that erasure feedback does not improve the worst-case regret upper bound order over the previously studied no-feedback setting. In particular, we prove a regret lower bound of $\Omega(\sqrt{KT} + K / (1 - \epsilon))$, where $K$ is the number of arms and $T$ the time horizon, that matches no-feedback upper bounds up to logarithmic factors. We note however that the availability of feedback enables simpler algorithm designs that may achieve better constants (albeit not better order) regret bounds; we design one such algorithm and evaluate its performance numerically.

Learning for Bandits under Action Erasures

We consider a novel multi-arm bandit (MAB) setup, where a learner needs to communicate the actions to distributed agents over erasure channels, while the rewards for the actions are directly available to the learner through external sensors. In our model, while the distributed agents know if an action is erased, the central learner does not (there is no feedback), and thus does not know whether the observed reward resulted from the desired action or not. We propose a scheme that can work on top of any (existing or future) MAB algorithm and make it robust to action erasures. Our scheme results in a worst-case regret over action-erasure channels that is at most a factor of $O(1/\sqrt{1-\epsilon})$ away from the no-erasure worst-case regret of the underlying MAB algorithm, where $\epsilon$ is the erasure probability. We also propose a modification of the successive arm elimination algorithm and prove that its worst-case regret is $\Tilde{O}(\sqrt{KT}+K/(1-\epsilon))$, which we prove is optimal by providing a matching lower bound.

Multi-Agent Bandit Learning through Heterogeneous Action Erasure Channels

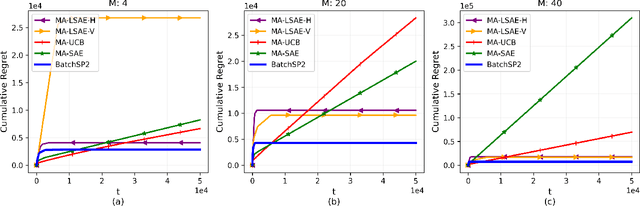
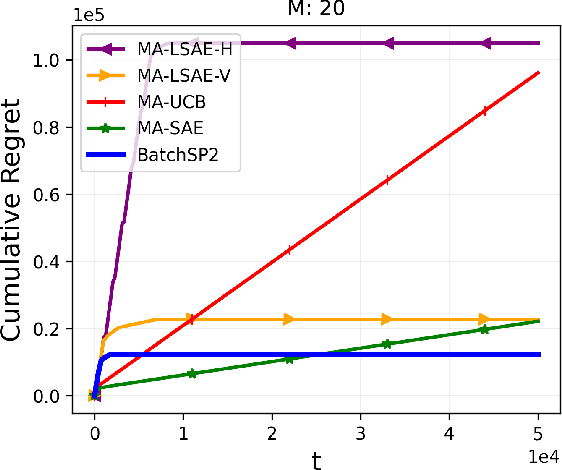
Multi-Armed Bandit (MAB) systems are witnessing an upswing in applications within multi-agent distributed environments, leading to the advancement of collaborative MAB algorithms. In such settings, communication between agents executing actions and the primary learner making decisions can hinder the learning process. A prevalent challenge in distributed learning is action erasure, often induced by communication delays and/or channel noise. This results in agents possibly not receiving the intended action from the learner, subsequently leading to misguided feedback. In this paper, we introduce novel algorithms that enable learners to interact concurrently with distributed agents across heterogeneous action erasure channels with different action erasure probabilities. We illustrate that, in contrast to existing bandit algorithms, which experience linear regret, our algorithms assure sub-linear regret guarantees. Our proposed solutions are founded on a meticulously crafted repetition protocol and scheduling of learning across heterogeneous channels. To our knowledge, these are the first algorithms capable of effectively learning through heterogeneous action erasure channels. We substantiate the superior performance of our algorithm through numerical experiments, emphasizing their practical significance in addressing issues related to communication constraints and delays in multi-agent environments.

Proactive Resilient Transmission and Scheduling Mechanisms for mmWave Networks

This paper aims to develop resilient transmission mechanisms to suitably distribute traffic across multiple paths in an arbitrary millimeter-wave (mmWave) network. The main contributions include: (a) the development of proactive transmission mechanisms that build resilience against network disruptions in advance, while achieving a high end-to-end packet rate; (b) the design of a heuristic path selection algorithm that efficiently selects (in polynomial time in the network size) multiple proactively resilient paths with high packet rates; and (c) the development of a hybrid scheduling algorithm that combines the proposed path selection algorithm with a deep reinforcement learning (DRL) based online approach for decentralized adaptation to blocked links and failed paths. To achieve resilience to link failures, a state-of-the-art Soft Actor-Critic DRL algorithm, which adapts the information flow through the network, is investigated. The proposed scheduling algorithm robustly adapts to link failures over different topologies, channel and blockage realizations while offering a superior performance to alternative algorithms.

Contexts can be Cheap: Solving Stochastic Contextual Bandits with Linear Bandit Algorithms

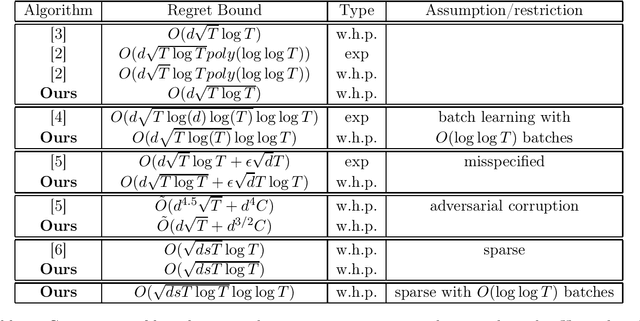
In this paper, we address the stochastic contextual linear bandit problem, where a decision maker is provided a context (a random set of actions drawn from a distribution). The expected reward of each action is specified by the inner product of the action and an unknown parameter. The goal is to design an algorithm that learns to play as close as possible to the unknown optimal policy after a number of action plays. This problem is considered more challenging than the linear bandit problem, which can be viewed as a contextual bandit problem with a \emph{fixed} context. Surprisingly, in this paper, we show that the stochastic contextual problem can be solved as if it is a linear bandit problem. In particular, we establish a novel reduction framework that converts every stochastic contextual linear bandit instance to a linear bandit instance, when the context distribution is known. When the context distribution is unknown, we establish an algorithm that reduces the stochastic contextual instance to a sequence of linear bandit instances with small misspecifications and achieves nearly the same worst-case regret bound as the algorithm that solves the misspecified linear bandit instances. As a consequence, our results imply a $O(d\sqrt{T\log T})$ high-probability regret bound for contextual linear bandits, making progress in resolving an open problem in (Li et al., 2019), (Li et al., 2021). Our reduction framework opens up a new way to approach stochastic contextual linear bandit problems, and enables improved regret bounds in a number of instances including the batch setting, contextual bandits with misspecifications, contextual bandits with sparse unknown parameters, and contextual bandits with adversarial corruption.

Differentially Private Stochastic Linear Bandits: (Almost) for Free

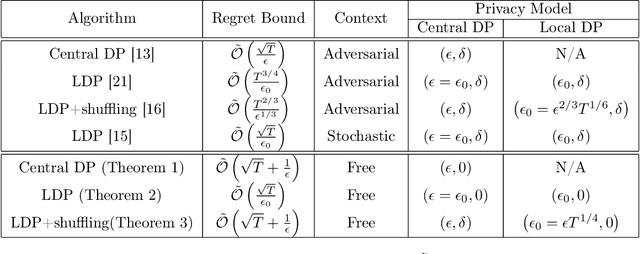
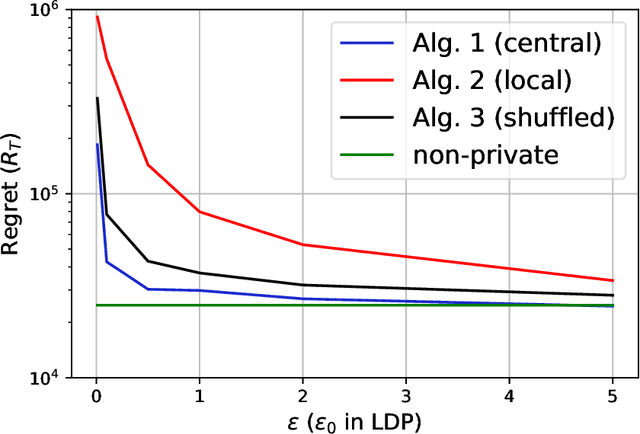
In this paper, we propose differentially private algorithms for the problem of stochastic linear bandits in the central, local and shuffled models. In the central model, we achieve almost the same regret as the optimal non-private algorithms, which means we get privacy for free. In particular, we achieve a regret of $\tilde{O}(\sqrt{T}+\frac{1}{\epsilon})$ matching the known lower bound for private linear bandits, while the best previously known algorithm achieves $\tilde{O}(\frac{1}{\epsilon}\sqrt{T})$. In the local case, we achieve a regret of $\tilde{O}(\frac{1}{\epsilon}{\sqrt{T}})$ which matches the non-private regret for constant $\epsilon$, but suffers a regret penalty when $\epsilon$ is small. In the shuffled model, we also achieve regret of $\tilde{O}(\sqrt{T}+\frac{1}{\epsilon})$ %for small $\epsilon$ as in the central case, while the best previously known algorithm suffers a regret of $\tilde{O}(\frac{1}{\epsilon}{T^{3/5}})$. Our numerical evaluation validates our theoretical results.

Learning in Distributed Contextual Linear Bandits Without Sharing the Context

Contextual linear bandits is a rich and theoretically important model that has many practical applications. Recently, this setup gained a lot of interest in applications over wireless where communication constraints can be a performance bottleneck, especially when the contexts come from a large $d$-dimensional space. In this paper, we consider a distributed memoryless contextual linear bandit learning problem, where the agents who observe the contexts and take actions are geographically separated from the learner who performs the learning while not seeing the contexts. We assume that contexts are generated from a distribution and propose a method that uses $\approx 5d$ bits per context for the case of unknown context distribution and $0$ bits per context if the context distribution is known, while achieving nearly the same regret bound as if the contexts were directly observable. The former bound improves upon existing bounds by a $\log(T)$ factor, where $T$ is the length of the horizon, while the latter achieves information theoretical tightness.

Solving Multi-Arm Bandit Using a Few Bits of Communication

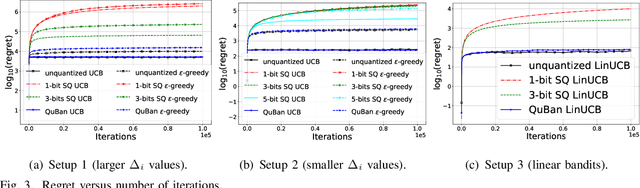
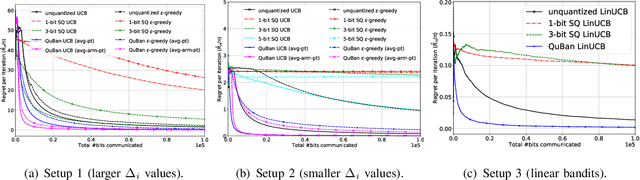
The multi-armed bandit (MAB) problem is an active learning framework that aims to select the best among a set of actions by sequentially observing rewards. Recently, it has become popular for a number of applications over wireless networks, where communication constraints can form a bottleneck. Existing works usually fail to address this issue and can become infeasible in certain applications. In this paper we address the communication problem by optimizing the communication of rewards collected by distributed agents. By providing nearly matching upper and lower bounds, we tightly characterize the number of bits needed per reward for the learner to accurately learn without suffering additional regret. In particular, we establish a generic reward quantization algorithm, QuBan, that can be applied on top of any (no-regret) MAB algorithm to form a new communication-efficient counterpart, that requires only a few (as low as 3) bits to be sent per iteration while preserving the same regret bound. Our lower bound is established via constructing hard instances from a subgaussian distribution. Our theory is further corroborated by numerically experiments.

A Reinforcement Learning Approach for Scheduling in mmWave Networks

We consider a source that wishes to communicate with a destination at a desired rate, over a mmWave network where links are subject to blockage and nodes to failure (e.g., in a hostile military environment). To achieve resilience to link and node failures, we here explore a state-of-the-art Soft Actor-Critic (SAC) deep reinforcement learning algorithm, that adapts the information flow through the network, without using knowledge of the link capacities or network topology. Numerical evaluations show that our algorithm can achieve the desired rate even in dynamic environments and it is robust against blockage.