Solving Multi-Arm Bandit Using a Few Bits of Communication
Paper and Code
Nov 11, 2021

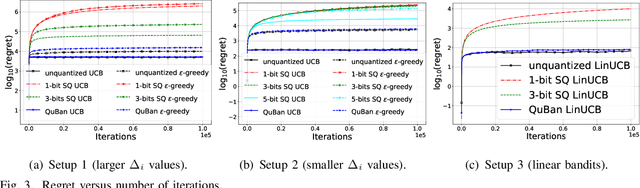
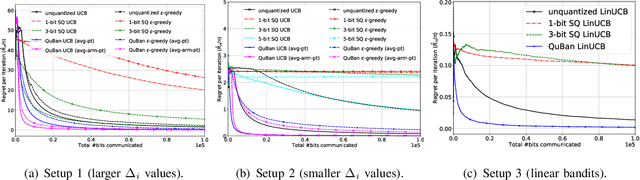
The multi-armed bandit (MAB) problem is an active learning framework that aims to select the best among a set of actions by sequentially observing rewards. Recently, it has become popular for a number of applications over wireless networks, where communication constraints can form a bottleneck. Existing works usually fail to address this issue and can become infeasible in certain applications. In this paper we address the communication problem by optimizing the communication of rewards collected by distributed agents. By providing nearly matching upper and lower bounds, we tightly characterize the number of bits needed per reward for the learner to accurately learn without suffering additional regret. In particular, we establish a generic reward quantization algorithm, QuBan, that can be applied on top of any (no-regret) MAB algorithm to form a new communication-efficient counterpart, that requires only a few (as low as 3) bits to be sent per iteration while preserving the same regret bound. Our lower bound is established via constructing hard instances from a subgaussian distribution. Our theory is further corroborated by numerically experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge