Hierarchical Bayes Approach to Personalized Federated Unsupervised Learning

Statistical heterogeneity of clients' local data is an important characteristic in federated learning, motivating personalized algorithms tailored to the local data statistics. Though there has been a plethora of algorithms proposed for personalized supervised learning, discovering the structure of local data through personalized unsupervised learning is less explored. We initiate a systematic study of such personalized unsupervised learning by developing algorithms based on optimization criteria inspired by a hierarchical Bayesian statistical framework. We develop adaptive algorithms that discover the balance between using limited local data and collaborative information. We do this in the context of two unsupervised learning tasks: personalized dimensionality reduction and personalized diffusion models. We develop convergence analyses for our adaptive algorithms which illustrate the dependence on problem parameters (e.g., heterogeneity, local sample size). We also develop a theoretical framework for personalized diffusion models, which shows the benefits of collaboration even under heterogeneity. We finally evaluate our proposed algorithms using synthetic and real data, demonstrating the effective sample amplification for personalized tasks, induced through collaboration, despite data heterogeneity.

MADA: Meta-Adaptive Optimizers through hyper-gradient Descent

Since Adam was introduced, several novel adaptive optimizers for deep learning have been proposed. These optimizers typically excel in some tasks but may not outperform Adam uniformly across all tasks. In this work, we introduce Meta-Adaptive Optimizers (MADA), a unified optimizer framework that can generalize several known optimizers and dynamically learn the most suitable one during training. The key idea in MADA is to parameterize the space of optimizers and search through it using hyper-gradient descent. Numerical results suggest that MADA is robust against sub-optimally tuned hyper-parameters, and outperforms Adam, Lion, and Adan with their default hyper-parameters, often even with optimized hyper-parameters. We also propose AVGrad, a variant of AMSGrad where the maximum operator is replaced with averaging, and observe that it performs better within MADA. Finally, we provide a convergence analysis to show that interpolation of optimizers (specifically, AVGrad and Adam) can improve their error bounds (up to constants), hinting at an advantage for meta-optimizers.

A Generative Framework for Personalized Learning and Estimation: Theory, Algorithms, and Privacy

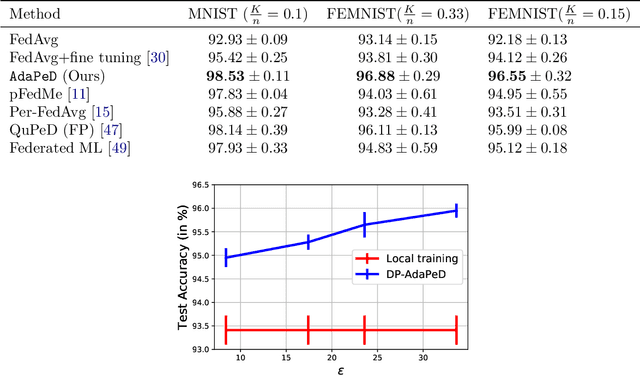
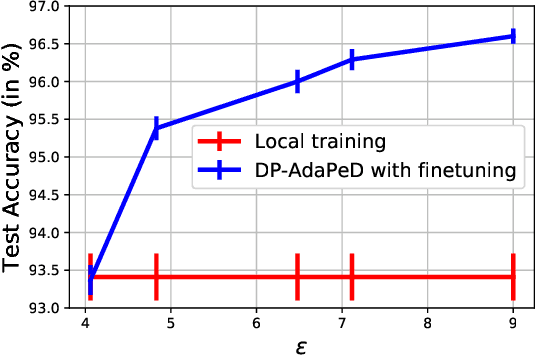
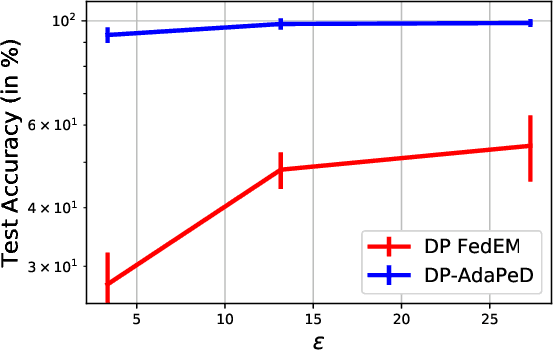
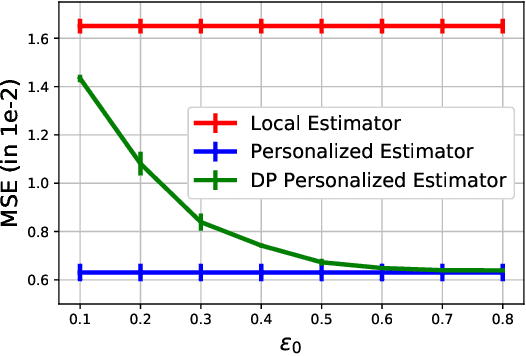
A distinguishing characteristic of federated learning is that the (local) client data could have statistical heterogeneity. This heterogeneity has motivated the design of personalized learning, where individual (personalized) models are trained, through collaboration. There have been various personalization methods proposed in literature, with seemingly very different forms and methods ranging from use of a single global model for local regularization and model interpolation, to use of multiple global models for personalized clustering, etc. In this work, we begin with a generative framework that could potentially unify several different algorithms as well as suggest new algorithms. We apply our generative framework to personalized estimation, and connect it to the classical empirical Bayes' methodology. We develop private personalized estimation under this framework. We then use our generative framework for learning, which unifies several known personalized FL algorithms and also suggests new ones; we propose and study a new algorithm AdaPeD based on a Knowledge Distillation, which numerically outperforms several known algorithms. We also develop privacy for personalized learning methods with guarantees for user-level privacy and composition. We numerically evaluate the performance as well as the privacy for both the estimation and learning problems, demonstrating the advantages of our proposed methods.

QuPeD: Quantized Personalization via Distillation with Applications to Federated Learning

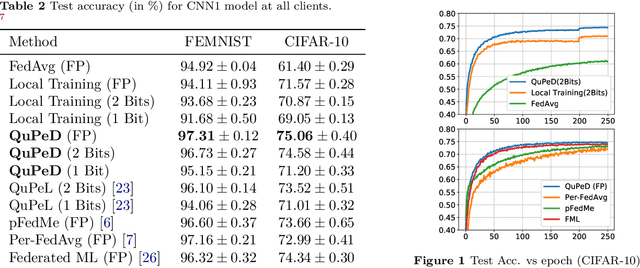
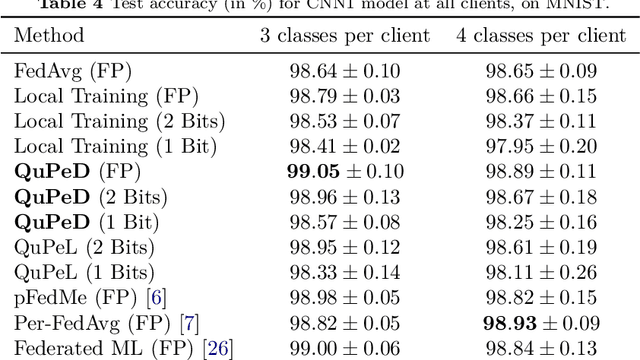
Traditionally, federated learning (FL) aims to train a single global model while collaboratively using multiple clients and a server. Two natural challenges that FL algorithms face are heterogeneity in data across clients and collaboration of clients with {\em diverse resources}. In this work, we introduce a \textit{quantized} and \textit{personalized} FL algorithm QuPeD that facilitates collective (personalized model compression) training via \textit{knowledge distillation} (KD) among clients who have access to heterogeneous data and resources. For personalization, we allow clients to learn \textit{compressed personalized models} with different quantization parameters and model dimensions/structures. Towards this, first we propose an algorithm for learning quantized models through a relaxed optimization problem, where quantization values are also optimized over. When each client participating in the (federated) learning process has different requirements for the compressed model (both in model dimension and precision), we formulate a compressed personalization framework by introducing knowledge distillation loss for local client objectives collaborating through a global model. We develop an alternating proximal gradient update for solving this compressed personalization problem, and analyze its convergence properties. Numerically, we validate that QuPeD outperforms competing personalized FL methods, FedAvg, and local training of clients in various heterogeneous settings.

QuPeL: Quantized Personalization with Applications to Federated Learning

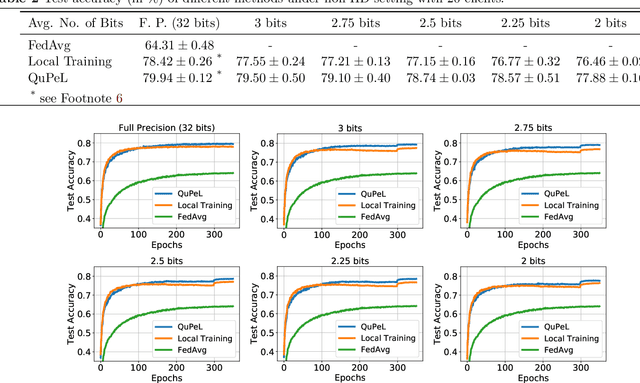
Traditionally, federated learning (FL) aims to train a single global model while collaboratively using multiple clients and a server. Two natural challenges that FL algorithms face are heterogeneity in data across clients and collaboration of clients with {\em diverse resources}. In this work, we introduce a \textit{quantized} and \textit{personalized} FL algorithm QuPeL that facilitates collective training with heterogeneous clients while respecting resource diversity. For personalization, we allow clients to learn \textit{compressed personalized models} with different quantization parameters depending on their resources. Towards this, first we propose an algorithm for learning quantized models through a relaxed optimization problem, where quantization values are also optimized over. When each client participating in the (federated) learning process has different requirements of the quantized model (both in value and precision), we formulate a quantized personalization framework by introducing a penalty term for local client objectives against a globally trained model to encourage collaboration. We develop an alternating proximal gradient update for solving this quantized personalization problem, and we analyze its convergence properties. Numerically, we show that optimizing over the quantization levels increases the performance and we validate that QuPeL outperforms both FedAvg and local training of clients in a heterogeneous setting.