Representation Transfer Learning via Multiple Pre-trained models for Linear Regression

In this paper, we consider the problem of learning a linear regression model on a data domain of interest (target) given few samples. To aid learning, we are provided with a set of pre-trained regression models that are trained on potentially different data domains (sources). Assuming a representation structure for the data generating linear models at the sources and the target domains, we propose a representation transfer based learning method for constructing the target model. The proposed scheme is comprised of two phases: (i) utilizing the different source representations to construct a representation that is adapted to the target data, and (ii) using the obtained model as an initialization to a fine-tuning procedure that re-trains the entire (over-parameterized) regression model on the target data. For each phase of the training method, we provide excess risk bounds for the learned model compared to the true data generating target model. The derived bounds show a gain in sample complexity for our proposed method compared to the baseline method of not leveraging source representations when achieving the same excess risk, therefore, theoretically demonstrating the effectiveness of transfer learning for linear regression.

Semantic rule Web-based Diagnosis and Treatment of Vector-Borne Diseases using SWRL rules

Vector-borne diseases (VBDs) are a kind of infection caused through the transmission of vectors generated by the bites of infected parasites, bacteria, and viruses, such as ticks, mosquitoes, triatomine bugs, blackflies, and sandflies. If these diseases are not properly treated within a reasonable time frame, the mortality rate may rise. In this work, we propose a set of ontologies that will help in the diagnosis and treatment of vector-borne diseases. For developing VBD's ontology, electronic health records taken from the Indian Health Records website, text data generated from Indian government medical mobile applications, and doctors' prescribed handwritten notes of patients are used as input. This data is then converted into correct text using Optical Character Recognition (OCR) and a spelling checker after pre-processing. Natural Language Processing (NLP) is applied for entity extraction from text data for making Resource Description Framework (RDF) medical data with the help of the Patient Clinical Data (PCD) ontology. Afterwards, Basic Formal Ontology (BFO), National Vector Borne Disease Control Program (NVBDCP) guidelines, and RDF medical data are used to develop ontologies for VBDs, and Semantic Web Rule Language (SWRL) rules are applied for diagnosis and treatment. The developed ontology helps in the construction of decision support systems (DSS) for the NVBDCP to control these diseases.

Alternating Mahalanobis Distance Minimization for Stable and Accurate CP Decomposition

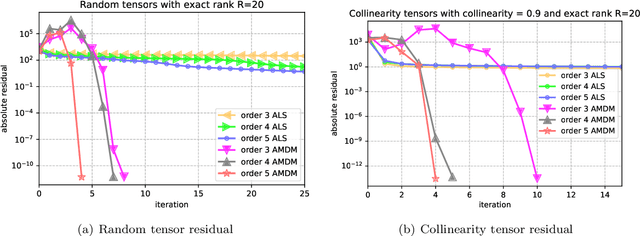
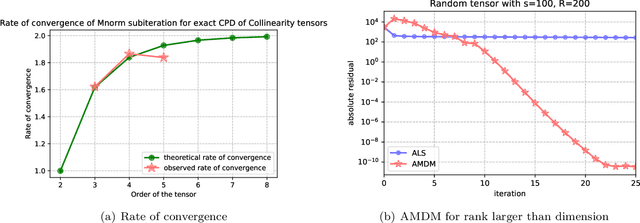
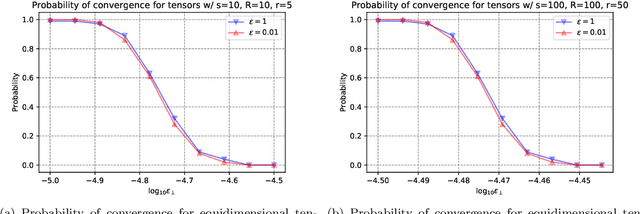
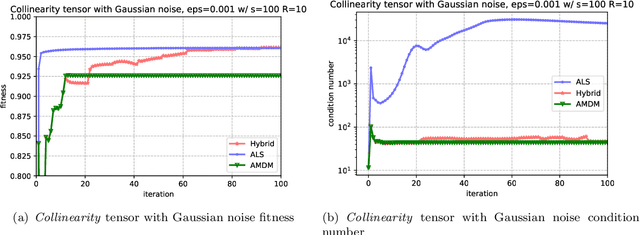
CP decomposition (CPD) is prevalent in chemometrics, signal processing, data mining and many more fields. While many algorithms have been proposed to compute the CPD, alternating least squares (ALS) remains one of the most widely used algorithm for computing the decomposition. Recent works have introduced the notion of eigenvalues and singular values of a tensor and explored applications of eigenvectors and singular vectors in areas like signal processing, data analytics and in various other fields. We introduce a new formulation for deriving singular values and vectors of a tensor by considering the critical points of a function different from what is used in the previous work. Computing these critical points in an alternating manner motivates an alternating optimization algorithm which corresponds to alternating least squares algorithm in the matrix case. However, for tensors with order greater than equal to $3$, it minimizes an objective function which is different from the commonly used least squares loss. Alternating optimization of this new objective leads to simple updates to the factor matrices with the same asymptotic computational cost as ALS. We show that a subsweep of this algorithm can achieve a superlinear convergence rate for exact CPD with known rank and verify it experimentally. We then view the algorithm as optimizing a Mahalanobis distance with respect to each factor with ground metric dependent on the other factors. This perspective allows us to generalize our approach to interpolate between updates corresponding to the ALS and the new algorithm to manage the tradeoff between stability and fitness of the decomposition. Our experimental results show that for approximating synthetic and real-world tensors, this algorithm and its variants converge to a better conditioned decomposition with comparable and sometimes better fitness as compared to the ALS algorithm.

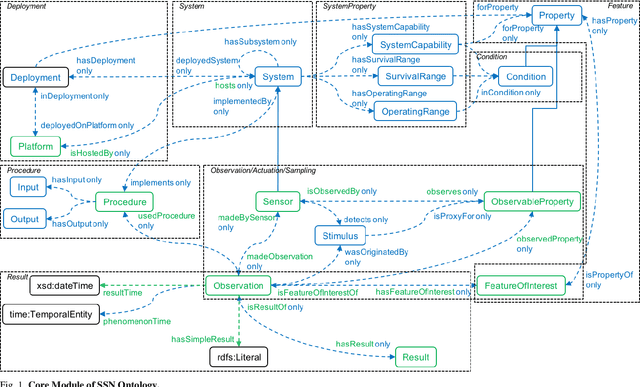
Semantic Sensor Network Ontology based Decision Support System for Forest Fire Management

The forests are significant assets for every country. When it gets destroyed, it may negatively impact the environment, and forest fire is one of the primary causes. Fire weather indices are widely used to measure fire danger and are used to issue bushfire warnings. It can also be used to predict the demand for emergency management resources. Sensor networks have grown in popularity in data collection and processing capabilities for a variety of applications in industries such as medical, environmental monitoring, home automation etc. Semantic sensor networks can collect various climatic circumstances like wind speed, temperature, and relative humidity. However, estimating fire weather indices is challenging due to the various issues involved in processing the data streams generated by the sensors. Hence, the importance of forest fire detection has increased day by day. The underlying Semantic Sensor Network (SSN) ontologies are built to allow developers to create rules for calculating fire weather indices and also the convert dataset into Resource Description Framework (RDF). This research describes the various steps involved in developing rules for calculating fire weather indices. Besides, this work presents a Web-based mapping interface to help users visualize the changes in fire weather indices over time. With the help of the inference rule, it designed a decision support system using the SSN ontology and query on it through SPARQL. The proposed fire management system acts according to the situation, supports reasoning and the general semantics of the open-world followed by all the ontologies

Decentralized Multi-Task Stochastic Optimization With Compressed Communications

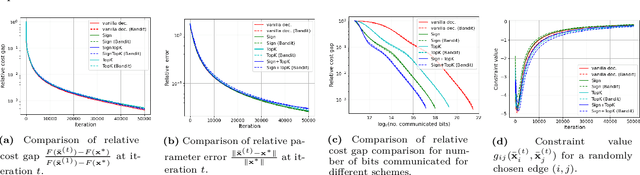
We consider a multi-agent network where each node has a stochastic (local) cost function that depends on the decision variable of that node and a random variable, and further the decision variables of neighboring nodes are pairwise constrained. There is an aggregate objective function for the network, composed additively of the expected values of the local cost functions at the nodes, and the overall goal of the network is to obtain the minimizing solution to this aggregate objective function subject to all the pairwise constraints. This is to be achieved at the node level using decentralized information and local computation, with exchanges of only compressed information allowed by neighboring nodes. The paper develops algorithms and obtains performance bounds for two different models of local information availability at the nodes: (i) sample feedback, where each node has direct access to samples of the local random variable to evaluate its local cost, and (ii) bandit feedback, where samples of the random variables are not available, but only the values of the local cost functions at two random points close to the decision are available to each node. For both models, with compressed communication between neighbors, we have developed decentralized saddle-point algorithms that deliver performances no different (in order sense) from those without communication compression; specifically, we show that deviation from the global minimum value and violations of the constraints are upper-bounded by $\mathcal{O}(T^{-\frac{1}{2}})$ and $\mathcal{O}(T^{-\frac{1}{4}})$, respectively, where $T$ is the number of iterations. Numerical examples provided in the paper corroborate these bounds and demonstrate the communication efficiency of the proposed method.

QuPeD: Quantized Personalization via Distillation with Applications to Federated Learning

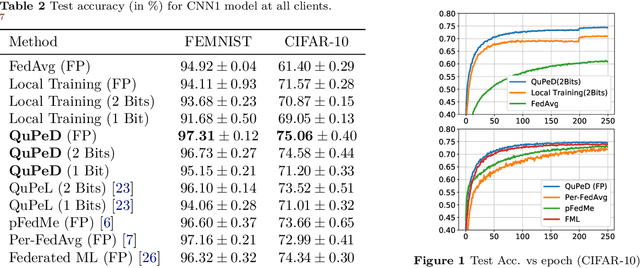
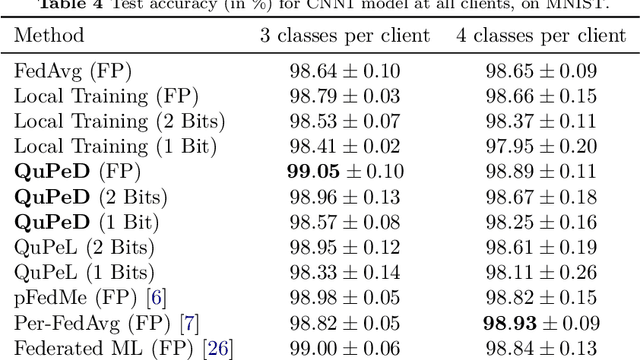
Traditionally, federated learning (FL) aims to train a single global model while collaboratively using multiple clients and a server. Two natural challenges that FL algorithms face are heterogeneity in data across clients and collaboration of clients with {\em diverse resources}. In this work, we introduce a \textit{quantized} and \textit{personalized} FL algorithm QuPeD that facilitates collective (personalized model compression) training via \textit{knowledge distillation} (KD) among clients who have access to heterogeneous data and resources. For personalization, we allow clients to learn \textit{compressed personalized models} with different quantization parameters and model dimensions/structures. Towards this, first we propose an algorithm for learning quantized models through a relaxed optimization problem, where quantization values are also optimized over. When each client participating in the (federated) learning process has different requirements for the compressed model (both in model dimension and precision), we formulate a compressed personalization framework by introducing knowledge distillation loss for local client objectives collaborating through a global model. We develop an alternating proximal gradient update for solving this compressed personalization problem, and analyze its convergence properties. Numerically, we validate that QuPeD outperforms competing personalized FL methods, FedAvg, and local training of clients in various heterogeneous settings.

Augmented Tensor Decomposition with Stochastic Optimization

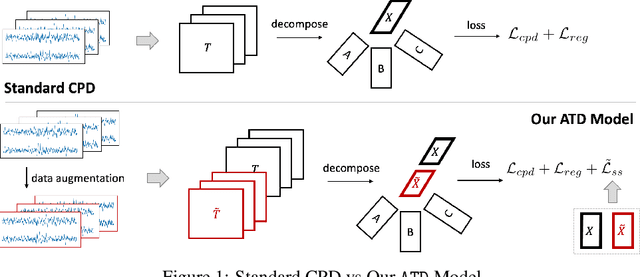
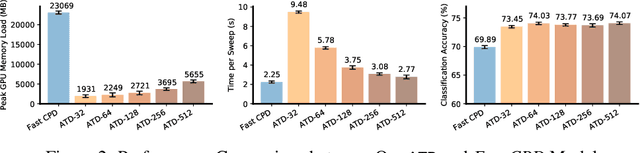
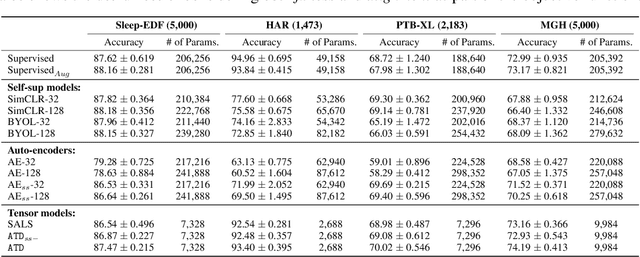
Tensor decompositions are powerful tools for dimensionality reduction and feature interpretation of multidimensional data such as signals. Existing tensor decomposition objectives (e.g., Frobenius norm) are designed for fitting raw data under statistical assumptions, which may not align with downstream classification tasks. Also, real-world tensor data are usually high-ordered and have large dimensions with millions or billions of entries. Thus, it is expensive to decompose the whole tensor with traditional algorithms. In practice, raw tensor data also contains redundant information while data augmentation techniques may be used to smooth out noise in samples. This paper addresses the above challenges by proposing augmented tensor decomposition (ATD), which effectively incorporates data augmentations to boost downstream classification. To reduce the memory footprint of the decomposition, we propose a stochastic algorithm that updates the factor matrices in a batch fashion. We evaluate ATD on multiple signal datasets. It shows comparable or better performance (e.g., up to 15% in accuracy) over self-supervised and autoencoder baselines with less than 5% of model parameters, achieves 0.6% ~ 1.3% accuracy gain over other tensor-based baselines, and reduces the memory footprint by 9X when compared to standard tensor decomposition algorithms.

MTC: Multiresolution Tensor Completion from Partial and Coarse Observations

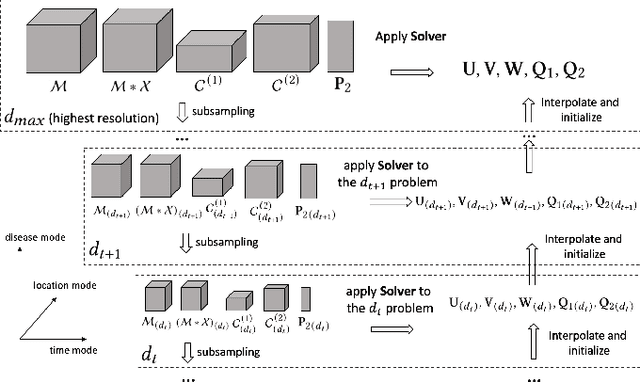
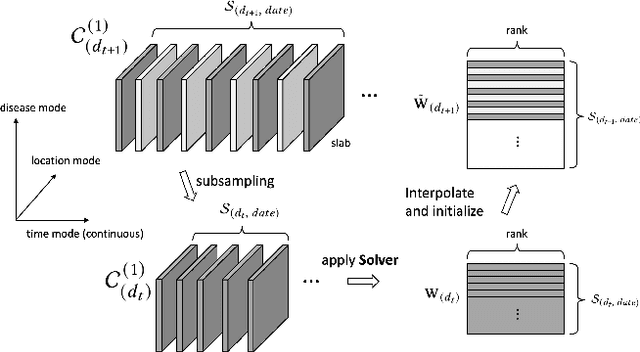
Existing tensor completion formulation mostly relies on partial observations from a single tensor. However, tensors extracted from real-world data are often more complex due to: (i) Partial observation: Only a small subset (e.g., 5%) of tensor elements are available. (ii) Coarse observation: Some tensor modes only present coarse and aggregated patterns (e.g., monthly summary instead of daily reports). In this paper, we are given a subset of the tensor and some aggregated/coarse observations (along one or more modes) and seek to recover the original fine-granular tensor with low-rank factorization. We formulate a coupled tensor completion problem and propose an efficient Multi-resolution Tensor Completion model (MTC) to solve the problem. Our MTC model explores tensor mode properties and leverages the hierarchy of resolutions to recursively initialize an optimization setup, and optimizes on the coupled system using alternating least squares. MTC ensures low computational and space complexity. We evaluate our model on two COVID-19 related spatio-temporal tensors. The experiments show that MTC could provide 65.20% and 75.79% percentage of fitness (PoF) in tensor completion with only 5% fine granular observations, which is 27.96% relative improvement over the best baseline. To evaluate the learned low-rank factors, we also design a tensor prediction task for daily and cumulative disease case predictions, where MTC achieves 50% in PoF and 30% relative improvements over the best baseline.

QuPeL: Quantized Personalization with Applications to Federated Learning

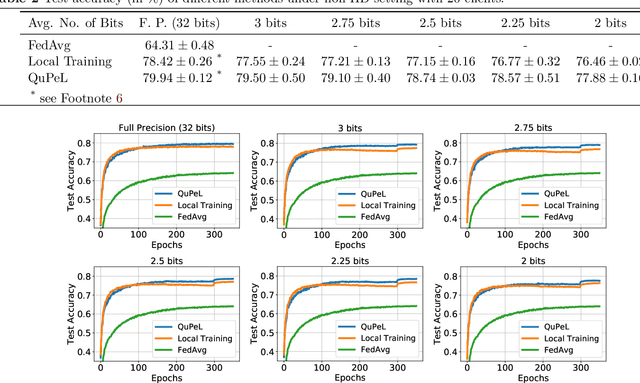
Traditionally, federated learning (FL) aims to train a single global model while collaboratively using multiple clients and a server. Two natural challenges that FL algorithms face are heterogeneity in data across clients and collaboration of clients with {\em diverse resources}. In this work, we introduce a \textit{quantized} and \textit{personalized} FL algorithm QuPeL that facilitates collective training with heterogeneous clients while respecting resource diversity. For personalization, we allow clients to learn \textit{compressed personalized models} with different quantization parameters depending on their resources. Towards this, first we propose an algorithm for learning quantized models through a relaxed optimization problem, where quantization values are also optimized over. When each client participating in the (federated) learning process has different requirements of the quantized model (both in value and precision), we formulate a quantized personalization framework by introducing a penalty term for local client objectives against a globally trained model to encourage collaboration. We develop an alternating proximal gradient update for solving this quantized personalization problem, and we analyze its convergence properties. Numerically, we show that optimizing over the quantization levels increases the performance and we validate that QuPeL outperforms both FedAvg and local training of clients in a heterogeneous setting.

SQuARM-SGD: Communication-Efficient Momentum SGD for Decentralized Optimization

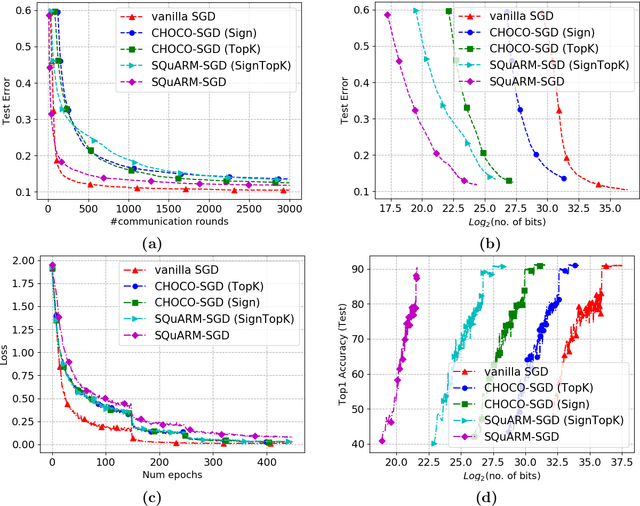
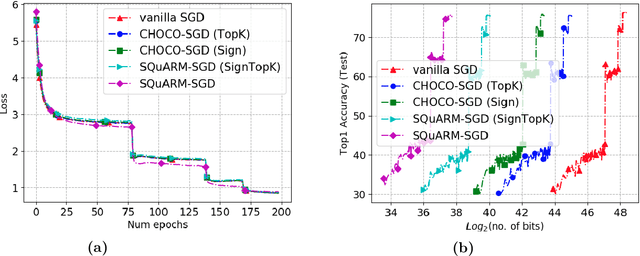
In this paper, we consider the problem of communication-efficient decentralized training of large-scale machine learning models over a network. We propose and analyze SQuARM-SGD, an algorithm for decentralized training, which employs {\em momentum} and {\em compressed communication} between nodes regulated by a locally computable triggering condition in stochastic gradient descent (SGD). In SQuARM-SGD, each node performs a fixed number of local SGD steps using Nesterov's momentum and then sends sparisified and quantized updates to its neighbors only when there is a significant change in the model parameters since the last time communication occurred. We provide convergence guarantees of our algorithm for (smooth) strongly convex and non-convex objectives, and show that SQuARM-SGD converges at a rate of $\mathcal{O}\left(\nicefrac{1}{nT}\right)$ for strongly convex objectives, while for non-convex objectives it convergences at a rate of $\mathcal{O}\left(\nicefrac{1}{\sqrt{nT}}\right)$, thus matching the convergence rate of \emph{vanilla} distributed SGD in both these settings. We corroborate our theoretical understanding with experiments and compare the performance of our algorithm with the state-of-the-art, showing that without sacrificing much on the accuracy, SQuARM-SGD converges at a similar rate while saving significantly in total communicated bits.