Decentralized Nonconvex Optimization with Guaranteed Privacy and Accuracy

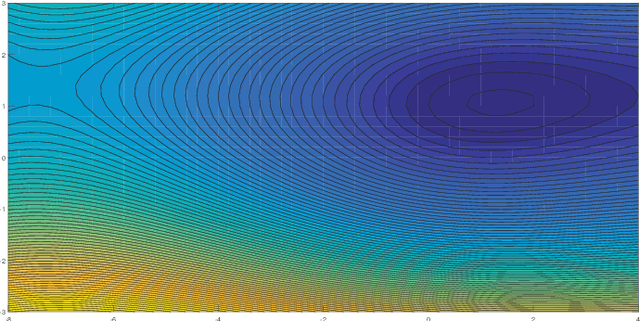
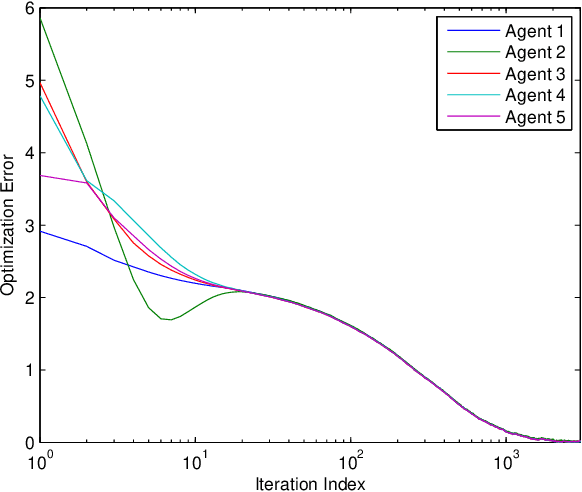
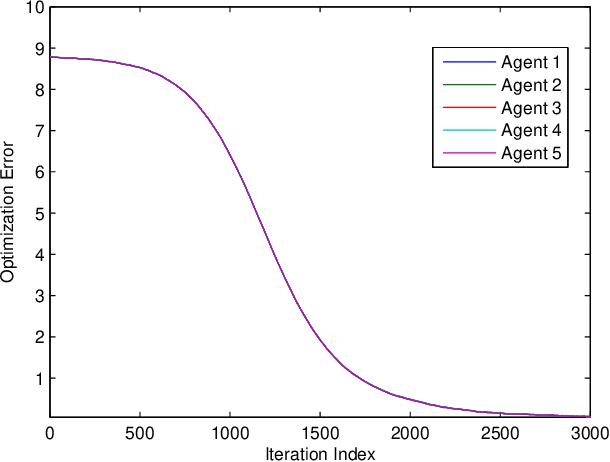
Privacy protection and nonconvexity are two challenging problems in decentralized optimization and learning involving sensitive data. Despite some recent advances addressing each of the two problems separately, no results have been reported that have theoretical guarantees on both privacy protection and saddle/maximum avoidance in decentralized nonconvex optimization. We propose a new algorithm for decentralized nonconvex optimization that can enable both rigorous differential privacy and saddle/maximum avoiding performance. The new algorithm allows the incorporation of persistent additive noise to enable rigorous differential privacy for data samples, gradients, and intermediate optimization variables without losing provable convergence, and thus circumventing the dilemma of trading accuracy for privacy in differential privacy design. More interestingly, the algorithm is theoretically proven to be able to efficiently { guarantee accuracy by avoiding} convergence to local maxima and saddle points, which has not been reported before in the literature on decentralized nonconvex optimization. The algorithm is efficient in both communication (it only shares one variable in each iteration) and computation (it is encryption-free), and hence is promising for large-scale nonconvex optimization and learning involving high-dimensional optimization parameters. Numerical experiments for both a decentralized estimation problem and an Independent Component Analysis (ICA) problem confirm the effectiveness of the proposed approach.

Quantization enabled Privacy Protection in Decentralized Stochastic Optimization

By enabling multiple agents to cooperatively solve a global optimization problem in the absence of a central coordinator, decentralized stochastic optimization is gaining increasing attention in areas as diverse as machine learning, control, and sensor networks. Since the associated data usually contain sensitive information, such as user locations and personal identities, privacy protection has emerged as a crucial need in the implementation of decentralized stochastic optimization. In this paper, we propose a decentralized stochastic optimization algorithm that is able to guarantee provable convergence accuracy even in the presence of aggressive quantization errors that are proportional to the amplitude of quantization inputs. The result applies to both convex and non-convex objective functions, and enables us to exploit aggressive quantization schemes to obfuscate shared information, and hence enables privacy protection without losing provable optimization accuracy. In fact, by using a {stochastic} ternary quantization scheme, which quantizes any value to three numerical levels, we achieve quantization-based rigorous differential privacy in decentralized stochastic optimization, which has not been reported before. In combination with the presented quantization scheme, the proposed algorithm ensures, for the first time, rigorous differential privacy in decentralized stochastic optimization without losing provable convergence accuracy. Simulation results for a distributed estimation problem as well as numerical experiments for decentralized learning on a benchmark machine learning dataset confirm the effectiveness of the proposed approach.

Decentralized Multi-Task Stochastic Optimization With Compressed Communications

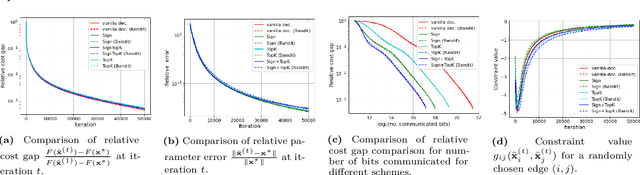
We consider a multi-agent network where each node has a stochastic (local) cost function that depends on the decision variable of that node and a random variable, and further the decision variables of neighboring nodes are pairwise constrained. There is an aggregate objective function for the network, composed additively of the expected values of the local cost functions at the nodes, and the overall goal of the network is to obtain the minimizing solution to this aggregate objective function subject to all the pairwise constraints. This is to be achieved at the node level using decentralized information and local computation, with exchanges of only compressed information allowed by neighboring nodes. The paper develops algorithms and obtains performance bounds for two different models of local information availability at the nodes: (i) sample feedback, where each node has direct access to samples of the local random variable to evaluate its local cost, and (ii) bandit feedback, where samples of the random variables are not available, but only the values of the local cost functions at two random points close to the decision are available to each node. For both models, with compressed communication between neighbors, we have developed decentralized saddle-point algorithms that deliver performances no different (in order sense) from those without communication compression; specifically, we show that deviation from the global minimum value and violations of the constraints are upper-bounded by $\mathcal{O}(T^{-\frac{1}{2}})$ and $\mathcal{O}(T^{-\frac{1}{4}})$, respectively, where $T$ is the number of iterations. Numerical examples provided in the paper corroborate these bounds and demonstrate the communication efficiency of the proposed method.

Decentralized Q-Learning in Zero-sum Markov Games

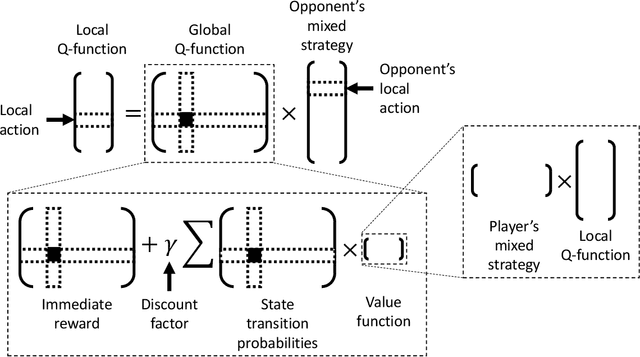
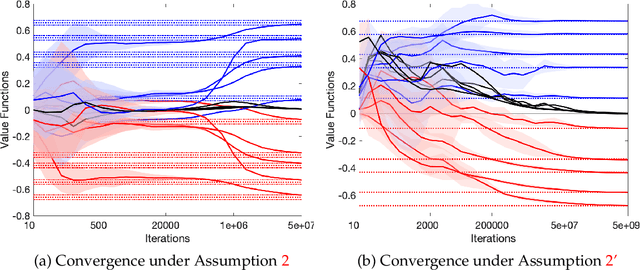
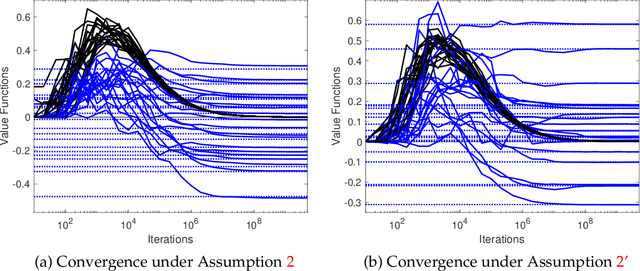
We study multi-agent reinforcement learning (MARL) in infinite-horizon discounted zero-sum Markov games. We focus on the practical but challenging setting of decentralized MARL, where agents make decisions without coordination by a centralized controller, but only based on their own payoffs and local actions executed. The agents need not observe the opponent's actions or payoffs, possibly being even oblivious to the presence of the opponent, nor be aware of the zero-sum structure of the underlying game, a setting also referred to as radically uncoupled in the literature of learning in games. In this paper, we develop for the first time a radically uncoupled Q-learning dynamics that is both rational and convergent: the learning dynamics converges to the best response to the opponent's strategy when the opponent follows an asymptotically stationary strategy; the value function estimates converge to the payoffs at a Nash equilibrium when both agents adopt the dynamics. The key challenge in this decentralized setting is the non-stationarity of the learning environment from an agent's perspective, since both her own payoffs and the system evolution depend on the actions of other agents, and each agent adapts their policies simultaneously and independently. To address this issue, we develop a two-timescale learning dynamics where each agent updates her local Q-function and value function estimates concurrently, with the latter happening at a slower timescale.

The Confluence of Networks, Games and Learning

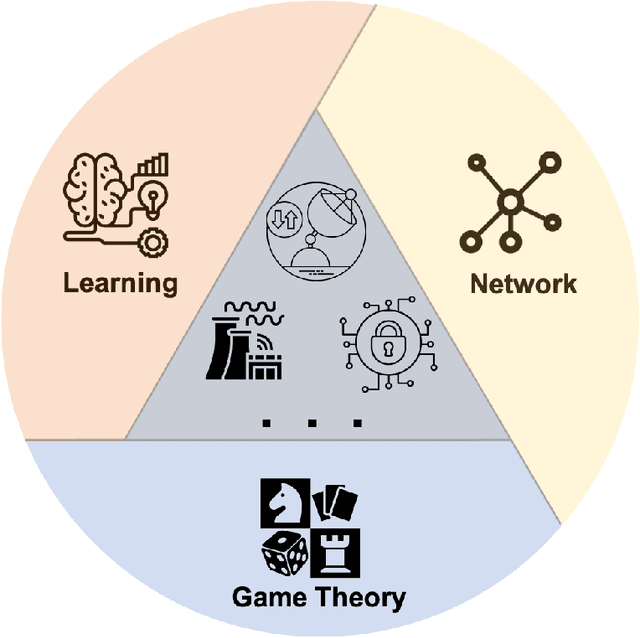
Recent years have witnessed significant advances in technologies and services in modern network applications, including smart grid management, wireless communication, cybersecurity as well as multi-agent autonomous systems. Considering the heterogeneous nature of networked entities, emerging network applications call for game-theoretic models and learning-based approaches in order to create distributed network intelligence that responds to uncertainties and disruptions in a dynamic or an adversarial environment. This paper articulates the confluence of networks, games and learning, which establishes a theoretical underpinning for understanding multi-agent decision-making over networks. We provide an selective overview of game-theoretic learning algorithms within the framework of stochastic approximation theory, and associated applications in some representative contexts of modern network systems, such as the next generation wireless communication networks, the smart grid and distributed machine learning. In addition to existing research works on game-theoretic learning over networks, we highlight several new angles and research endeavors on learning in games that are related to recent developments in artificial intelligence. Some of the new angles extrapolate from our own research interests. The overall objective of the paper is to provide the reader a clear picture of the strengths and challenges of adopting game-theoretic learning methods within the context of network systems, and further to identify fruitful future research directions on both theoretical and applied studies.

A Multi-Agent Off-Policy Actor-Critic Algorithm for Distributed Reinforcement Learning

This paper extends off-policy reinforcement learning to the multi-agent case in which a set of networked agents communicating with their neighbors according to a time-varying graph collaboratively evaluates and improves a target policy while following a distinct behavior policy. To this end, the paper develops a multi-agent version of emphatic temporal difference learning for off-policy policy evaluation, and proves convergence under linear function approximation. The paper then leverages this result, in conjunction with a novel multi-agent off-policy policy gradient theorem and recent work in both multi-agent on-policy and single-agent off-policy actor-critic methods, to develop and give convergence guarantees for a new multi-agent off-policy actor-critic algorithm.

A Game Theoretical Error-Correction Framework for Secure Traffic-Sign Classification

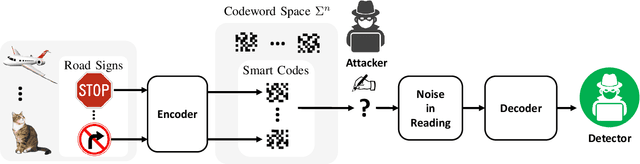
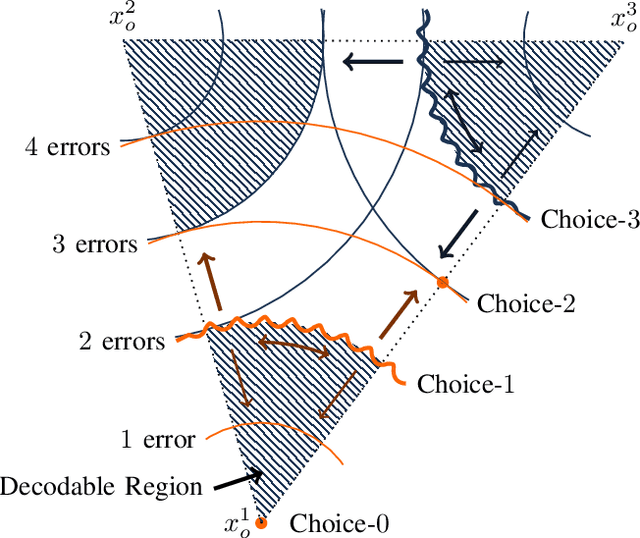
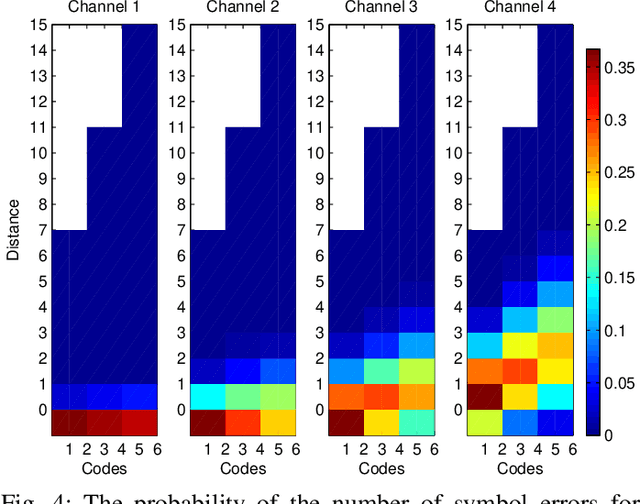
We introduce a game theoretical error-correction framework to design classification algorithms that are reliable even in adversarial environments, with a specific focus on traffic-sign classification. Machine learning algorithms possess inherent vulnerabilities against maliciously crafted inputs especially at high dimensional input spaces. We seek to achieve reliable and timely performance in classification by redesigning the input space physically to significantly lower dimensions. Traffic-sign classification is an important use-case enabling the redesign of the inputs since traffic-signs have already been designed for their easy recognition by human drivers. We encode the original input samples to, e.g., strings of bits, through error-correction methods that can provide certain distance guarantees in-between any two different encoded inputs. And we model the interaction between the defense and the adversary as a game. Then, we analyze the underlying game using the concept of hierarchical equilibrium, where the defense strategies are designed by taking into account the best possible attack against them. At large scale, for computational simplicity, we provide an approximate solution, where we transform the problem into an efficient linear program with substantially small size compared to the original size of the entire input space. Finally, we examine the performance of the proposed scheme over different traffic-sign classification scenarios.

Game-Theoretic Analysis of the Hegselmann-Krause Model for Opinion Dynamics in Finite Dimensions

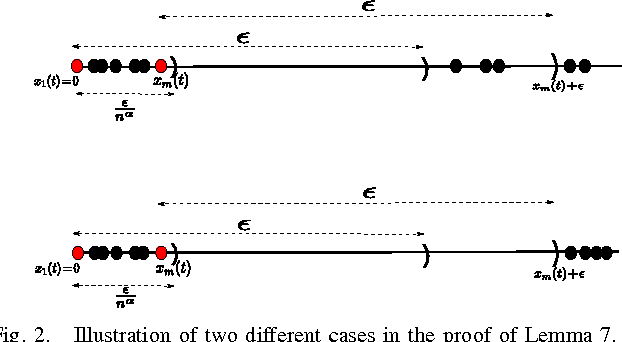
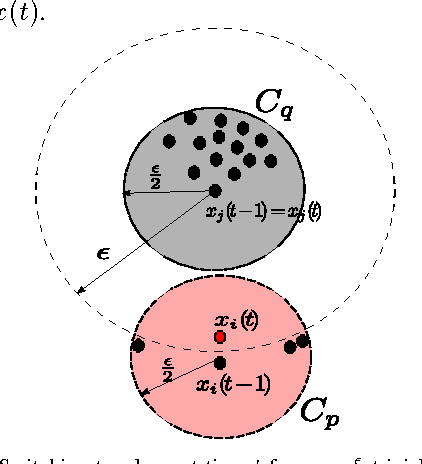
We consider the Hegselmann-Krause model for opinion dynamics and study the evolution of the system under various settings. We first analyze the termination time of the synchronous Hegselmann-Krause dynamics in arbitrary finite dimensions and show that the termination time in general only depends on the number of agents involved in the dynamics. To the best of our knowledge, that is the sharpest bound for the termination time of such dynamics that removes dependency of the termination time from the dimension of the ambient space. This answers an open question in [1] on how to obtain a tighter upper bound for the termination time. Furthermore, we study the asynchronous Hegselmann-Krause model from a novel game-theoretic approach and show that the evolution of an asynchronous Hegselmann-Krause model is equivalent to a sequence of best response updates in a well-designed potential game. We then provide a polynomial upper bound for the expected time and expected number of switching topologies until the dynamic reaches an arbitrarily small neighborhood of its equilibrium points, provided that the agents update uniformly at random. This is a step toward analysis of heterogeneous Hegselmann-Krause dynamics. Finally, we consider the heterogeneous Hegselmann-Krause dynamics and provide a necessary condition for the finite termination time of such dynamics. In particular, we sketch some future directions toward more detailed analysis of the heterogeneous Hegselmann-Krause model.

Adaptive-Rate Compressive Sensing Using Side Information

We provide two novel adaptive-rate compressive sensing (CS) strategies for sparse, time-varying signals using side information. Our first method utilizes extra cross-validation measurements, and the second one exploits extra low-resolution measurements. Unlike the majority of current CS techniques, we do not assume that we know an upper bound on the number of significant coefficients that comprise the images in the video sequence. Instead, we use the side information to predict the number of significant coefficients in the signal at the next time instant. For each image in the video sequence, our techniques specify a fixed number of spatially-multiplexed CS measurements to acquire, and adjust this quantity from image to image. Our strategies are developed in the specific context of background subtraction for surveillance video, and we experimentally validate the proposed methods on real video sequences.

Lyapunov stochastic stability and control of robust dynamic coalitional games with transferable utilities

This paper considers a dynamic game with transferable utilities (TU), where the characteristic function is a continuous-time bounded mean ergodic process. A central planner interacts continuously over time with the players by choosing the instantaneous allocations subject to budget constraints. Before the game starts, the central planner knows the nature of the process (bounded mean ergodic), the bounded set from which the coalitions' values are sampled, and the long run average coalitions' values. On the other hand, he has no knowledge of the underlying probability function generating the coalitions' values. Our goal is to find allocation rules that use a measure of the extra reward that a coalition has received up to the current time by re-distributing the budget among the players. The objective is two-fold: i) guaranteeing convergence of the average allocations to the core (or a specific point in the core) of the average game, ii) driving the coalitions' excesses to an a priori given cone. The resulting allocation rules are robust as they guarantee the aforementioned convergence properties despite the uncertain and time-varying nature of the coaltions' values. We highlight three main contributions. First, we design an allocation rule based on full observation of the extra reward so that the average allocation approaches a specific point in the core of the average game, while the coalitions' excesses converge to an a priori given direction. Second, we design a new allocation rule based on partial observation on the extra reward so that the average allocation converges to the core of the average game, while the coalitions' excesses converge to an a priori given cone. And third, we establish connections to approachability theory and attainability theory.