Stochastic Convergence Results for Regularized Actor-Critic Methods

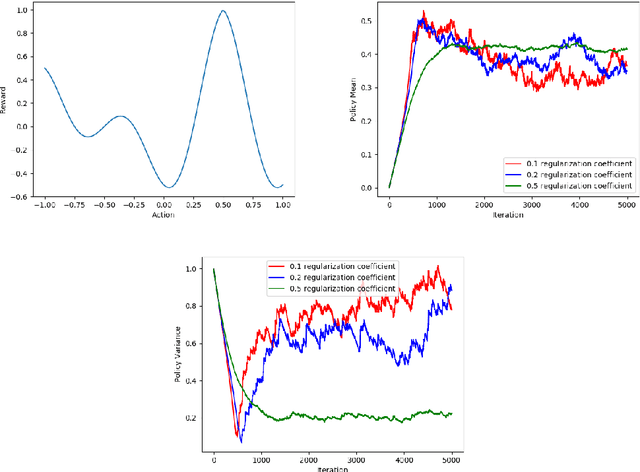
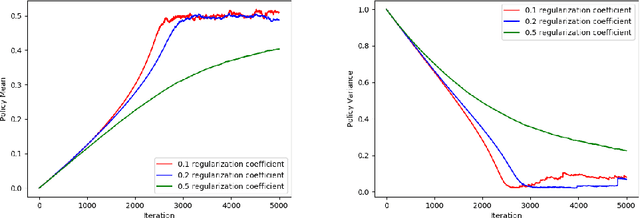
In this paper, we present a stochastic convergence proof, under suitable conditions, of a certain class of actor-critic algorithms for finding approximate solutions to entropy-regularized MDPs using the machinery of stochastic approximation. To obtain this overall result, we provide three fundamental results that are all of both practical and theoretical interest: we prove the convergence of policy evaluation with general regularizers when using linear approximation architectures, we derive an entropy-regularized policy gradient theorem, and we show convergence of entropy-regularized policy improvement. We also provide a simple, illustrative empirical study corroborating our theoretical results. To the best of our knowledge, this is the first time such results have been provided for approximate solution methods for regularized MDPs.

A Multi-Agent Off-Policy Actor-Critic Algorithm for Distributed Reinforcement Learning

This paper extends off-policy reinforcement learning to the multi-agent case in which a set of networked agents communicating with their neighbors according to a time-varying graph collaboratively evaluates and improves a target policy while following a distinct behavior policy. To this end, the paper develops a multi-agent version of emphatic temporal difference learning for off-policy policy evaluation, and proves convergence under linear function approximation. The paper then leverages this result, in conjunction with a novel multi-agent off-policy policy gradient theorem and recent work in both multi-agent on-policy and single-agent off-policy actor-critic methods, to develop and give convergence guarantees for a new multi-agent off-policy actor-critic algorithm.