Stochastic Convergence Results for Regularized Actor-Critic Methods

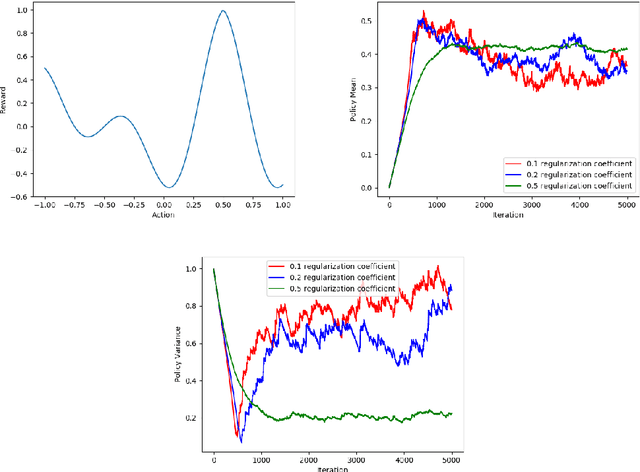
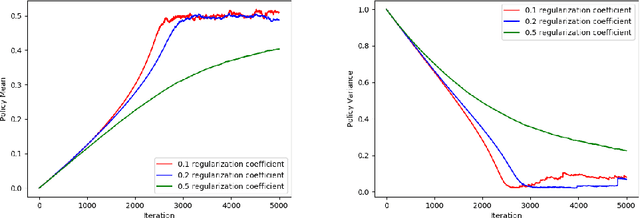
In this paper, we present a stochastic convergence proof, under suitable conditions, of a certain class of actor-critic algorithms for finding approximate solutions to entropy-regularized MDPs using the machinery of stochastic approximation. To obtain this overall result, we provide three fundamental results that are all of both practical and theoretical interest: we prove the convergence of policy evaluation with general regularizers when using linear approximation architectures, we derive an entropy-regularized policy gradient theorem, and we show convergence of entropy-regularized policy improvement. We also provide a simple, illustrative empirical study corroborating our theoretical results. To the best of our knowledge, this is the first time such results have been provided for approximate solution methods for regularized MDPs.