Strategizing against Q-learners: A Control-theoretical Approach

In this paper, we explore the susceptibility of the Q-learning algorithm (a classical and widely used reinforcement learning method) to strategic manipulation of sophisticated opponents in games. We quantify how much a strategically sophisticated agent can exploit a naive Q-learner if she knows the opponent's Q-learning algorithm. To this end, we formulate the strategic actor's problem as a Markov decision process (with a continuum state space encompassing all possible Q-values) as if the Q-learning algorithm is the underlying dynamical system. We also present a quantization-based approximation scheme to tackle the continuum state space and analyze its performance both analytically and numerically.

Efficient-Q Learning for Stochastic Games

We present the new efficient-Q learning dynamics for stochastic games beyond the recent concentration of progress on provable convergence to possibly inefficient equilibrium. We let agents follow the log-linear learning dynamics in stage games whose payoffs are the Q-functions and estimate the Q-functions iteratively with a vanishing stepsize. This (implicitly) two-timescale dynamic makes stage games relatively stationary for the log-linear update so that the agents can track the efficient equilibrium of stage games. We show that the Q-function estimates converge to the Q-function associated with the efficient equilibrium in identical-interest stochastic games, almost surely, with an approximation error induced by the softmax response in the log-linear update. The key idea is to approximate the dynamics with a fictional scenario where Q-function estimates are stationary over finite-length epochs. We then couple the dynamics in the main and fictional scenarios to show that the approximation error decays to zero due to the vanishing stepsize.

Independent Learning in Stochastic Games

Reinforcement learning (RL) has recently achieved tremendous successes in many artificial intelligence applications. Many of the forefront applications of RL involve multiple agents, e.g., playing chess and Go games, autonomous driving, and robotics. Unfortunately, the framework upon which classical RL builds is inappropriate for multi-agent learning, as it assumes an agent's environment is stationary and does not take into account the adaptivity of other agents. In this review paper, we present the model of stochastic games for multi-agent learning in dynamic environments. We focus on the development of simple and independent learning dynamics for stochastic games: each agent is myopic and chooses best-response type actions to other agents' strategy without any coordination with her opponent. There has been limited progress on developing convergent best-response type independent learning dynamics for stochastic games. We present our recently proposed simple and independent learning dynamics that guarantee convergence in zero-sum stochastic games, together with a review of other contemporaneous algorithms for dynamic multi-agent learning in this setting. Along the way, we also reexamine some classical results from both the game theory and RL literature, to situate both the conceptual contributions of our independent learning dynamics, and the mathematical novelties of our analysis. We hope this review paper serves as an impetus for the resurgence of studying independent and natural learning dynamics in game theory, for the more challenging settings with a dynamic environment.

Decentralized Q-Learning in Zero-sum Markov Games

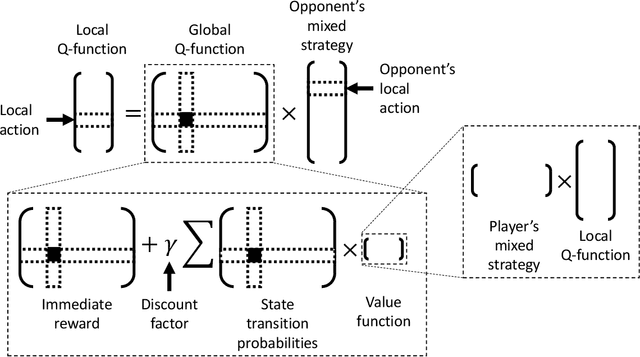
We study multi-agent reinforcement learning (MARL) in infinite-horizon discounted zero-sum Markov games. We focus on the practical but challenging setting of decentralized MARL, where agents make decisions without coordination by a centralized controller, but only based on their own payoffs and local actions executed. The agents need not observe the opponent's actions or payoffs, possibly being even oblivious to the presence of the opponent, nor be aware of the zero-sum structure of the underlying game, a setting also referred to as radically uncoupled in the literature of learning in games. In this paper, we develop for the first time a radically uncoupled Q-learning dynamics that is both rational and convergent: the learning dynamics converges to the best response to the opponent's strategy when the opponent follows an asymptotically stationary strategy; the value function estimates converge to the payoffs at a Nash equilibrium when both agents adopt the dynamics. The key challenge in this decentralized setting is the non-stationarity of the learning environment from an agent's perspective, since both her own payoffs and the system evolution depend on the actions of other agents, and each agent adapts their policies simultaneously and independently. To address this issue, we develop a two-timescale learning dynamics where each agent updates her local Q-function and value function estimates concurrently, with the latter happening at a slower timescale.

Fictitious play in zero-sum stochastic games

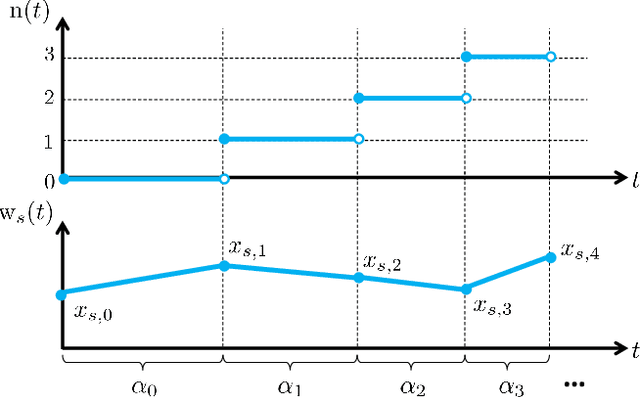
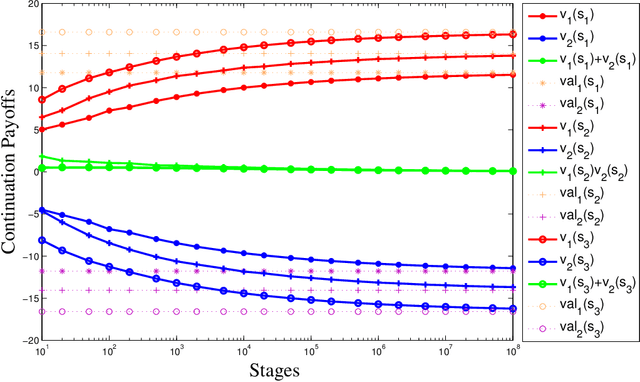
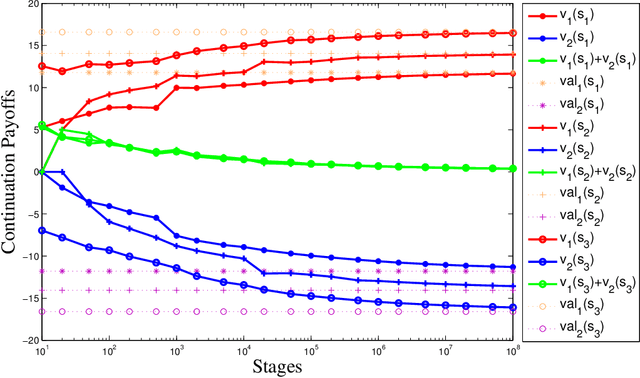
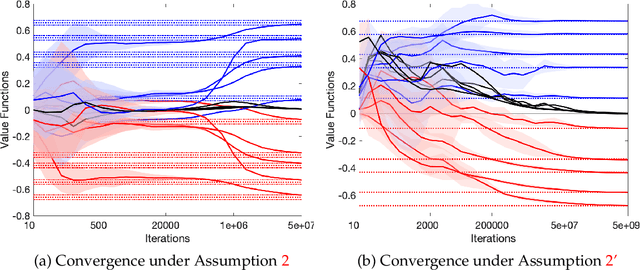
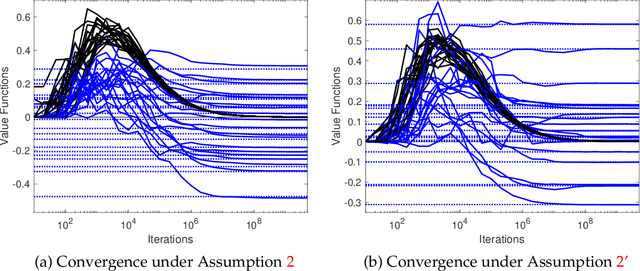
We present fictitious play dynamics for the general class of stochastic games and analyze its convergence properties in zero-sum stochastic games. Our dynamics involves agents forming beliefs on opponent strategy and their own continuation payoff (Q-function), and playing a myopic best response using estimated continuation payoffs. Agents update their beliefs at states visited from observations of opponent actions. A key property of the learning dynamics is that update of the beliefs on Q-functions occurs at a slower timescale than update of the beliefs on strategies. We show both in the model-based and model-free cases (without knowledge of agent payoff functions and state transition probabilities), the beliefs on strategies converge to a stationary mixed Nash equilibrium of the zero-sum stochastic game.

A Game Theoretical Error-Correction Framework for Secure Traffic-Sign Classification

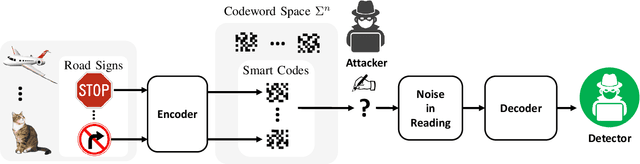
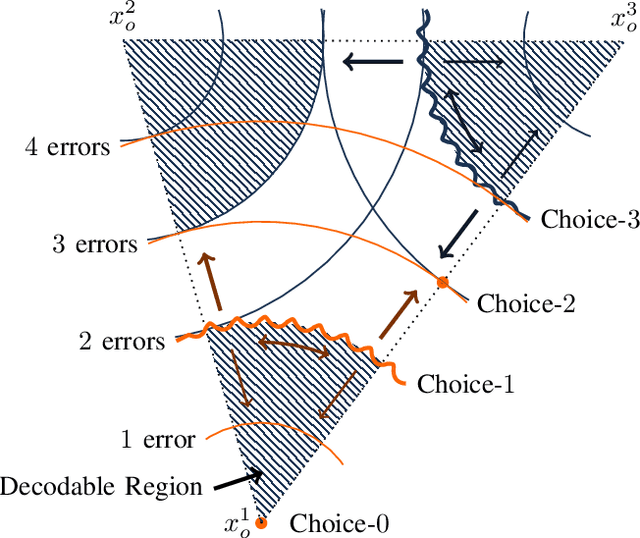
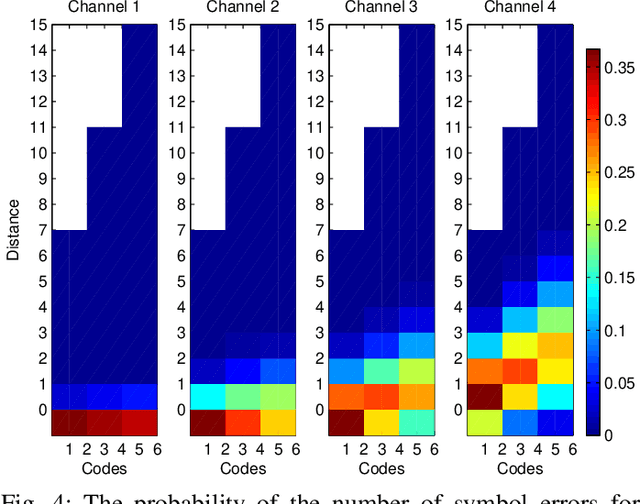
We introduce a game theoretical error-correction framework to design classification algorithms that are reliable even in adversarial environments, with a specific focus on traffic-sign classification. Machine learning algorithms possess inherent vulnerabilities against maliciously crafted inputs especially at high dimensional input spaces. We seek to achieve reliable and timely performance in classification by redesigning the input space physically to significantly lower dimensions. Traffic-sign classification is an important use-case enabling the redesign of the inputs since traffic-signs have already been designed for their easy recognition by human drivers. We encode the original input samples to, e.g., strings of bits, through error-correction methods that can provide certain distance guarantees in-between any two different encoded inputs. And we model the interaction between the defense and the adversary as a game. Then, we analyze the underlying game using the concept of hierarchical equilibrium, where the defense strategies are designed by taking into account the best possible attack against them. At large scale, for computational simplicity, we provide an approximate solution, where we transform the problem into an efficient linear program with substantially small size compared to the original size of the entire input space. Finally, we examine the performance of the proposed scheme over different traffic-sign classification scenarios.

Reliable Intersection Control in Non-cooperative Environments

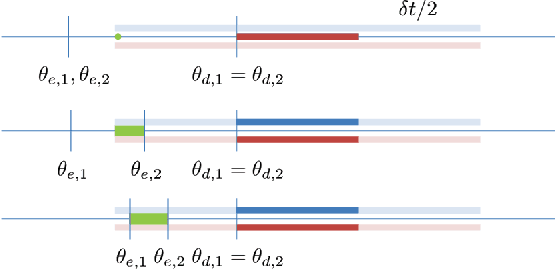
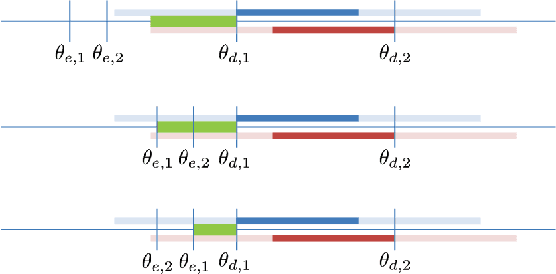
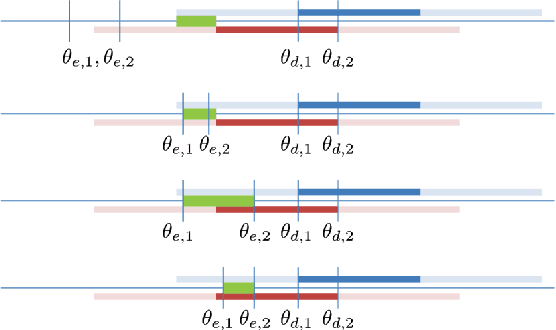
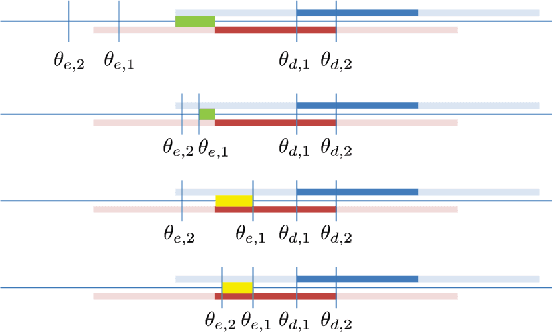
We propose a reliable intersection control mechanism for strategic autonomous and connected vehicles (agents) in non-cooperative environments. Each agent has access to his/her earliest possible and desired passing times, and reports a passing time to the intersection manager, who allocates the intersection temporally to the agents in a First-Come-First-Serve basis. However, the agents might have conflicting interests and can take actions strategically. To this end, we analyze the strategic behaviors of the agents and formulate Nash equilibria for all possible scenarios. Furthermore, among all Nash equilibria we identify a socially optimal equilibrium that leads to a fair intersection allocation, and correspondingly we describe a strategy-proof intersection mechanism, which achieves reliable intersection control such that the strategic agents do not have any incentive to misreport their passing times strategically.

Team-Optimal Distributed MMSE Estimation in General and Tree Networks

We construct team-optimal estimation algorithms over distributed networks for state estimation in the finite-horizon mean-square error (MSE) sense. Here, we have a distributed collection of agents with processing and cooperation capabilities. These agents observe noisy samples of a desired state through a linear model and seek to learn this state by interacting with each other. Although this problem has attracted significant attention and been studied extensively in fields including machine learning and signal processing, all the well-known strategies do not achieve team-optimal learning performance in the finite-horizon MSE sense. To this end, we formulate the finite-horizon distributed minimum MSE (MMSE) when there is no restriction on the size of the disclosed information, i.e., oracle performance, over an arbitrary network topology. Subsequently, we show that exchange of local estimates is sufficient to achieve the oracle performance only over certain network topologies. By inspecting these network structures, we propose recursive algorithms achieving the oracle performance through the disclosure of local estimates. For practical implementations we also provide approaches to reduce the complexity of the algorithms through the time-windowing of the observations. Finally, in the numerical examples, we demonstrate the superior performance of the introduced algorithms in the finite-horizon MSE sense due to optimal estimation.

Predicting Nearly As Well As the Optimal Twice Differentiable Regressor

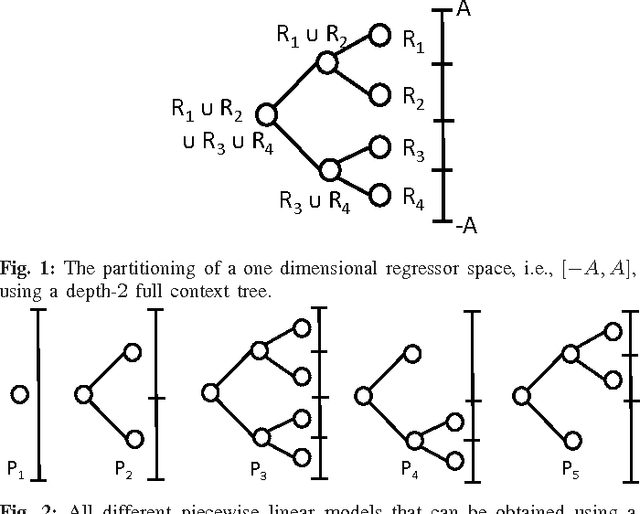
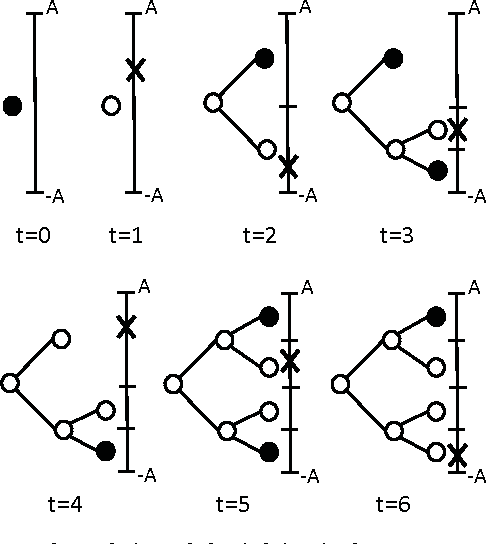
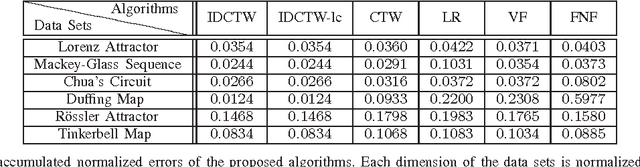
We study nonlinear regression of real valued data in an individual sequence manner, where we provide results that are guaranteed to hold without any statistical assumptions. We address the convergence and undertraining issues of conventional nonlinear regression methods and introduce an algorithm that elegantly mitigates these issues via an incremental hierarchical structure, (i.e., via an incremental decision tree). Particularly, we present a piecewise linear (or nonlinear) regression algorithm that partitions the regressor space in a data driven manner and learns a linear model at each region. Unlike the conventional approaches, our algorithm gradually increases the number of disjoint partitions on the regressor space in a sequential manner according to the observed data. Through this data driven approach, our algorithm sequentially and asymptotically achieves the performance of the optimal twice differentiable regression function for any data sequence with an unknown and arbitrary length. The computational complexity of the introduced algorithm is only logarithmic in the data length under certain regularity conditions. We provide the explicit description of the algorithm and demonstrate the significant gains for the well-known benchmark real data sets and chaotic signals.

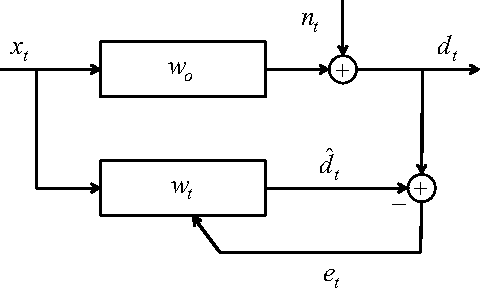
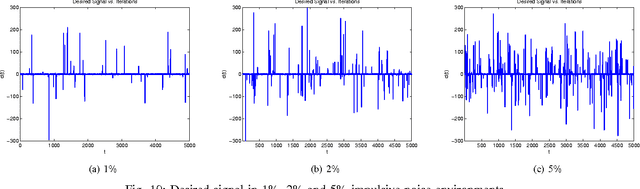
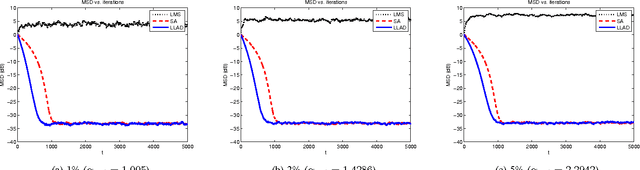
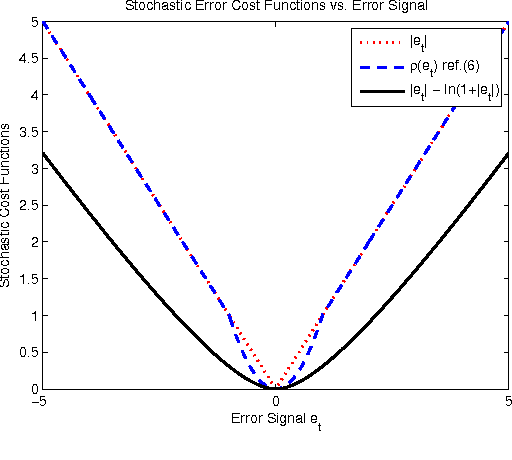
A Novel Family of Adaptive Filtering Algorithms Based on The Logarithmic Cost

We introduce a novel family of adaptive filtering algorithms based on a relative logarithmic cost. The new family intrinsically combines the higher and lower order measures of the error into a single continuous update based on the error amount. We introduce important members of this family of algorithms such as the least mean logarithmic square (LMLS) and least logarithmic absolute difference (LLAD) algorithms that improve the convergence performance of the conventional algorithms. However, our approach and analysis are generic such that they cover other well-known cost functions as described in the paper. The LMLS algorithm achieves comparable convergence performance with the least mean fourth (LMF) algorithm and extends the stability bound on the step size. The LLAD and least mean square (LMS) algorithms demonstrate similar convergence performance in impulse-free noise environments while the LLAD algorithm is robust against impulsive interferences and outperforms the sign algorithm (SA). We analyze the transient, steady state and tracking performance of the introduced algorithms and demonstrate the match of the theoretical analyzes and simulation results. We show the extended stability bound of the LMLS algorithm and analyze the robustness of the LLAD algorithm against impulsive interferences. Finally, we demonstrate the performance of our algorithms in different scenarios through numerical examples.