Data-Driven Approximations of Chance Constrained Programs in Nonstationary Environments

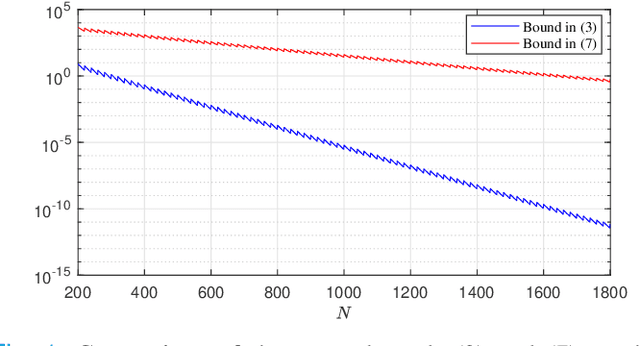
We study sample average approximations (SAA) of chance constrained programs. SAA methods typically approximate the actual distribution in the chance constraint using an empirical distribution constructed from random samples assumed to be independent and identically distributed according to the actual distribution. In this paper, we consider a nonstationary variant of this problem, where the random samples are assumed to be independently drawn in a sequential fashion from an unknown and possibly time-varying distribution. This nonstationarity may be driven by changing environmental conditions present in many real-world applications. To account for the potential nonstationarity in the data generation process, we propose a novel robust SAA method exploiting information about the Wasserstein distance between the sequence of data-generating distributions and the actual chance constraint distribution. As a key result, we obtain distribution-free estimates of the sample size required to ensure that the robust SAA method will yield solutions that are feasible for the chance constraint under the actual distribution with high confidence.

Fictitious play in zero-sum stochastic games

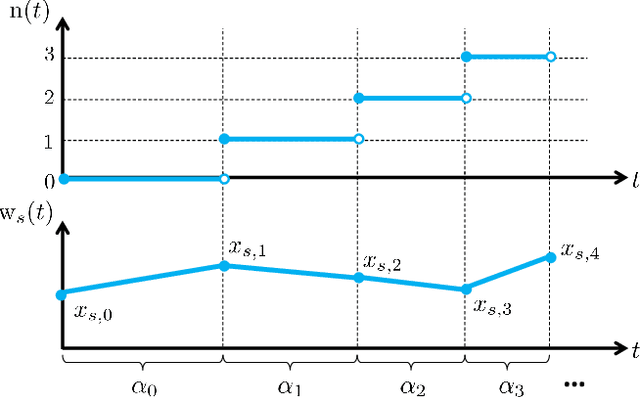
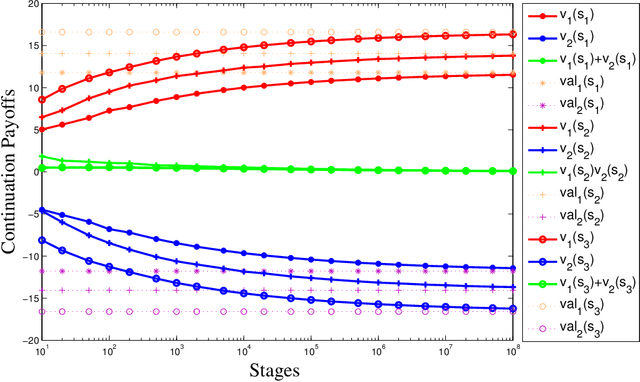
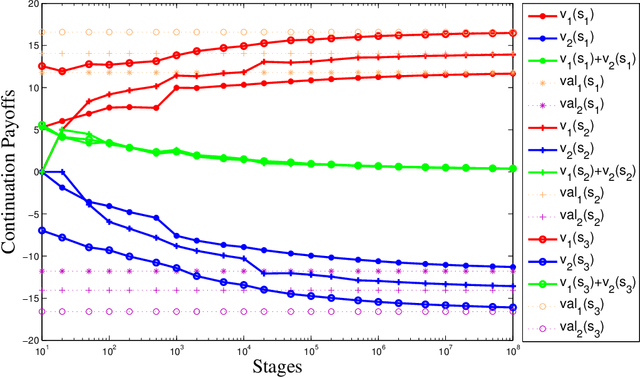
We present fictitious play dynamics for the general class of stochastic games and analyze its convergence properties in zero-sum stochastic games. Our dynamics involves agents forming beliefs on opponent strategy and their own continuation payoff (Q-function), and playing a myopic best response using estimated continuation payoffs. Agents update their beliefs at states visited from observations of opponent actions. A key property of the learning dynamics is that update of the beliefs on Q-functions occurs at a slower timescale than update of the beliefs on strategies. We show both in the model-based and model-free cases (without knowledge of agent payoff functions and state transition probabilities), the beliefs on strategies converge to a stationary mixed Nash equilibrium of the zero-sum stochastic game.

Centrality measures for graphons: Accounting for uncertainty in networks

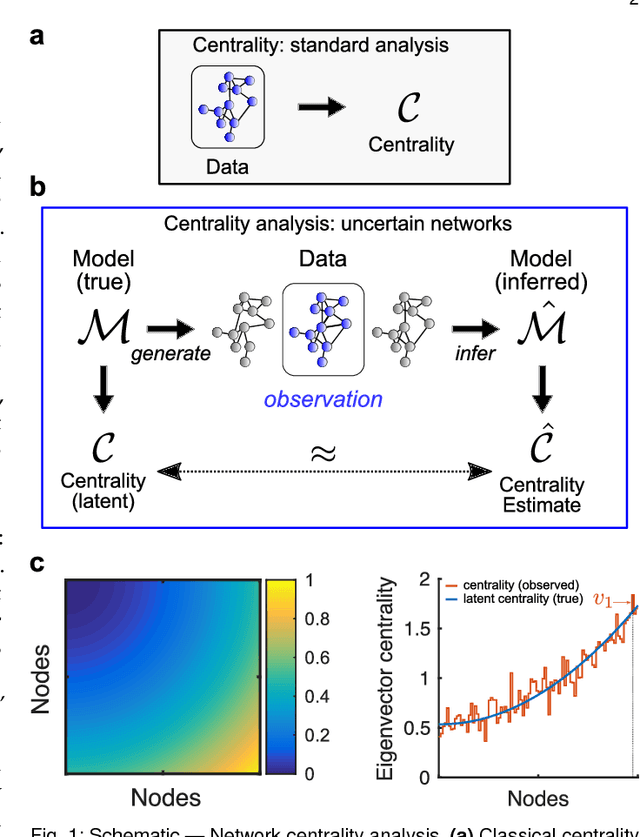
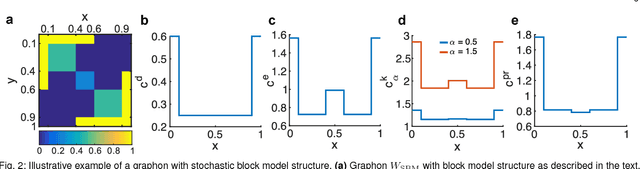
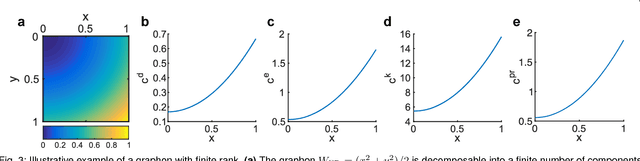
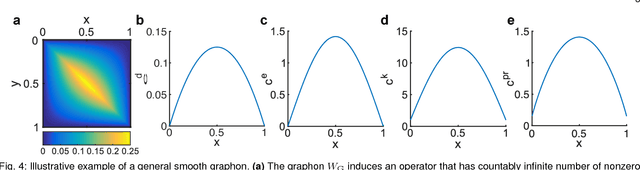
As relational datasets modeled as graphs keep increasing in size and their data-acquisition is permeated by uncertainty, graph-based analysis techniques can become computationally and conceptually challenging. In particular, node centrality measures rely on the assumption that the graph is perfectly known -- a premise not necessarily fulfilled for large, uncertain networks. Accordingly, centrality measures may fail to faithfully extract the importance of nodes in the presence of uncertainty. To mitigate these problems, we suggest a statistical approach based on graphon theory: we introduce formal definitions of centrality measures for graphons and establish their connections to classical graph centrality measures. A key advantage of this approach is that centrality measures defined at the modeling level of graphons are inherently robust to stochastic variations of specific graph realizations. Using the theory of linear integral operators, we define degree, eigenvector, Katz and PageRank centrality functions for graphons and establish concentration inequalities demonstrating that graphon centrality functions arise naturally as limits of their counterparts defined on sequences of graphs of increasing size. The same concentration inequalities also provide high-probability bounds between the graphon centrality functions and the centrality measures on any sampled graph, thereby establishing a measure of uncertainty of the measured centrality score.