A Distributionally Robust Approach to Regret Optimal Control using the Wasserstein Distance

This paper proposes a distributionally robust approach to regret optimal control of discrete-time linear dynamical systems with quadratic costs subject to stochastic additive disturbance on the state process. The underlying probability distribution of the disturbance process is unknown, but assumed to lie in a given ball of distributions defined in terms of the type-2 Wasserstein distance. In this framework, strictly causal linear disturbance feedback controllers are designed to minimize the worst-case expected regret. The regret incurred by a controller is defined as the difference between the cost it incurs in response to a realization of the disturbance process and the cost incurred by the optimal noncausal controller which has perfect knowledge of the disturbance process realization at the outset. Building on a well-established duality theory for optimal transport problems, we show how to equivalently reformulate this minimax regret optimal control problem as a tractable semidefinite program. The equivalent dual reformulation also allows us to characterize a worst-case distribution achieving the worst-case expected regret in relation to the distribution at the center of the Wasserstein ball.

Data-Driven Approximations of Chance Constrained Programs in Nonstationary Environments

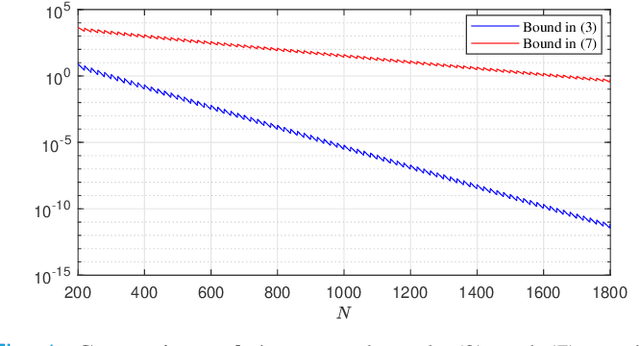
We study sample average approximations (SAA) of chance constrained programs. SAA methods typically approximate the actual distribution in the chance constraint using an empirical distribution constructed from random samples assumed to be independent and identically distributed according to the actual distribution. In this paper, we consider a nonstationary variant of this problem, where the random samples are assumed to be independently drawn in a sequential fashion from an unknown and possibly time-varying distribution. This nonstationarity may be driven by changing environmental conditions present in many real-world applications. To account for the potential nonstationarity in the data generation process, we propose a novel robust SAA method exploiting information about the Wasserstein distance between the sequence of data-generating distributions and the actual chance constraint distribution. As a key result, we obtain distribution-free estimates of the sample size required to ensure that the robust SAA method will yield solutions that are feasible for the chance constraint under the actual distribution with high confidence.