A Distributionally Robust Approach to Regret Optimal Control using the Wasserstein Distance

This paper proposes a distributionally robust approach to regret optimal control of discrete-time linear dynamical systems with quadratic costs subject to stochastic additive disturbance on the state process. The underlying probability distribution of the disturbance process is unknown, but assumed to lie in a given ball of distributions defined in terms of the type-2 Wasserstein distance. In this framework, strictly causal linear disturbance feedback controllers are designed to minimize the worst-case expected regret. The regret incurred by a controller is defined as the difference between the cost it incurs in response to a realization of the disturbance process and the cost incurred by the optimal noncausal controller which has perfect knowledge of the disturbance process realization at the outset. Building on a well-established duality theory for optimal transport problems, we show how to equivalently reformulate this minimax regret optimal control problem as a tractable semidefinite program. The equivalent dual reformulation also allows us to characterize a worst-case distribution achieving the worst-case expected regret in relation to the distribution at the center of the Wasserstein ball.

Data-Driven Approximations of Chance Constrained Programs in Nonstationary Environments

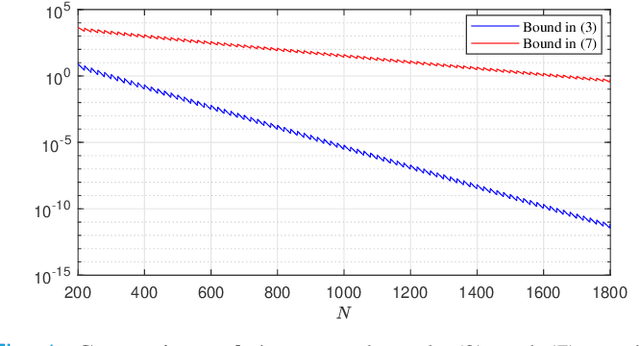
We study sample average approximations (SAA) of chance constrained programs. SAA methods typically approximate the actual distribution in the chance constraint using an empirical distribution constructed from random samples assumed to be independent and identically distributed according to the actual distribution. In this paper, we consider a nonstationary variant of this problem, where the random samples are assumed to be independently drawn in a sequential fashion from an unknown and possibly time-varying distribution. This nonstationarity may be driven by changing environmental conditions present in many real-world applications. To account for the potential nonstationarity in the data generation process, we propose a novel robust SAA method exploiting information about the Wasserstein distance between the sequence of data-generating distributions and the actual chance constraint distribution. As a key result, we obtain distribution-free estimates of the sample size required to ensure that the robust SAA method will yield solutions that are feasible for the chance constraint under the actual distribution with high confidence.

Exploring Adversarial Robustness of Multi-Sensor Perception Systems in Self Driving

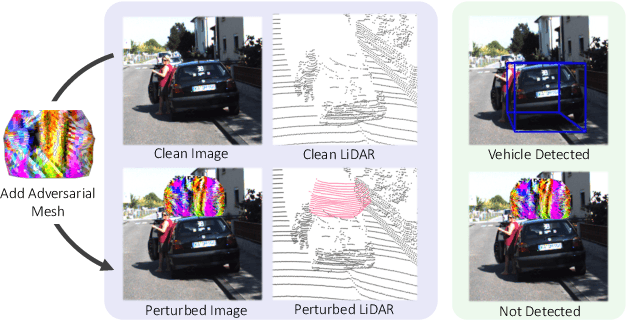
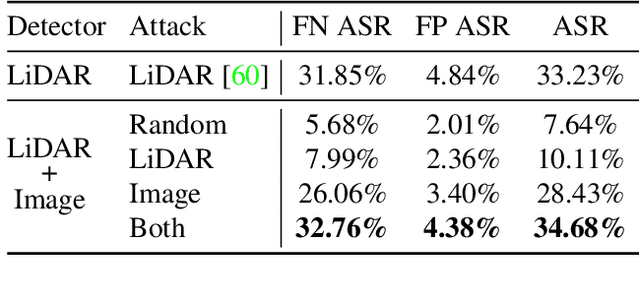
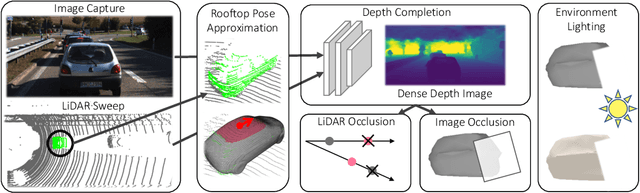
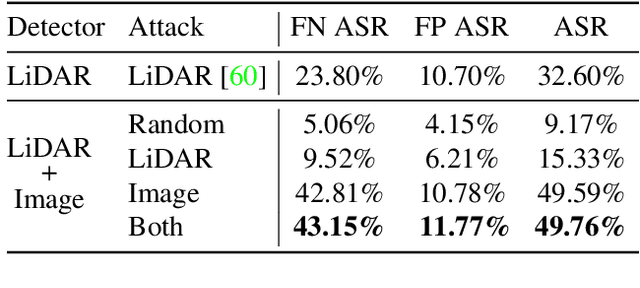
Modern self-driving perception systems have been shown to improve upon processing complementary inputs such as LiDAR with images. In isolation, 2D images have been found to be extremely vulnerable to adversarial attacks. Yet, there have been limited studies on the adversarial robustness of multi-modal models that fuse LiDAR features with image features. Furthermore, existing works do not consider physically realizable perturbations that are consistent across the input modalities. In this paper, we showcase practical susceptibilities of multi-sensor detection by placing an adversarial object on top of a host vehicle. We focus on physically realizable and input-agnostic attacks as they are feasible to execute in practice, and show that a single universal adversary can hide different host vehicles from state-of-the-art multi-modal detectors. Our experiments demonstrate that successful attacks are primarily caused by easily corrupted image features. Furthermore, we find that in modern sensor fusion methods which project image features into 3D, adversarial attacks can exploit the projection process to generate false positives across distant regions in 3D. Towards more robust multi-modal perception systems, we show that adversarial training with feature denoising can boost robustness to such attacks significantly. However, we find that standard adversarial defenses still struggle to prevent false positives which are also caused by inaccurate associations between 3D LiDAR points and 2D pixels.

Nonparametric Estimation of Uncertainty Sets for Robust Optimization

We investigate a data-driven approach to constructing uncertainty sets for robust optimization problems, where the uncertain problem parameters are modeled as random variables whose joint probability distribution is not known. Relying only on independent samples drawn from this distribution, we provide a nonparametric method to estimate uncertainty sets whose probability mass is guaranteed to approximate a given target mass within a given tolerance with high confidence. The nonparametric estimators that we consider are also shown to obey distribution-free finite-sample performance bounds that imply their convergence in probability to the given target mass. In addition to being efficient to compute, the proposed estimators result in uncertainty sets that yield computationally tractable robust optimization problems for a large family of constraint functions.

Safe Linear Stochastic Bandits

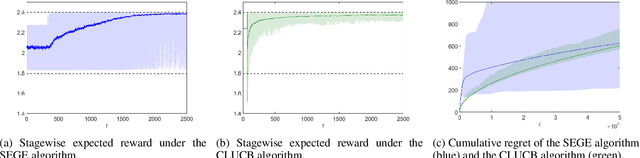
We introduce the safe linear stochastic bandit framework---a generalization of linear stochastic bandits---where, in each stage, the learner is required to select an arm with an expected reward that is no less than a predetermined (safe) threshold with high probability. We assume that the learner initially has knowledge of an arm that is known to be safe, but not necessarily optimal. Leveraging on this assumption, we introduce a learning algorithm that systematically combines known safe arms with exploratory arms to safely expand the set of safe arms over time, while facilitating safe greedy exploitation in subsequent stages. In addition to ensuring the satisfaction of the safety constraint at every stage of play, the proposed algorithm is shown to exhibit an expected regret that is no more than $O(\sqrt{T}\log (T))$ after $T$ stages of play.

Risk-Sensitive Learning and Pricing for Demand Response

We consider the setting in which an electric power utility seeks to curtail its peak electricity demand by offering a fixed group of customers a uniform price for reductions in consumption relative to their predetermined baselines. The underlying demand curve, which describes the aggregate reduction in consumption in response to the offered price, is assumed to be affine and subject to unobservable random shocks. Assuming that both the parameters of the demand curve and the distribution of the random shocks are initially unknown to the utility, we investigate the extent to which the utility might dynamically adjust its offered prices to maximize its cumulative risk-sensitive payoff over a finite number of $T$ days. In order to do so effectively, the utility must design its pricing policy to balance the tradeoff between the need to learn the unknown demand model (exploration) and maximize its payoff (exploitation) over time. In this paper, we propose such a pricing policy, which is shown to exhibit an expected payoff loss over $T$ days that is at most $O(\sqrt{T}\log(T))$, relative to an oracle pricing policy that knows the underlying demand model. Moreover, the proposed pricing policy is shown to yield a sequence of prices that converge to the oracle optimal prices in the mean square sense.

An Online Learning Approach to Buying and Selling Demand Response

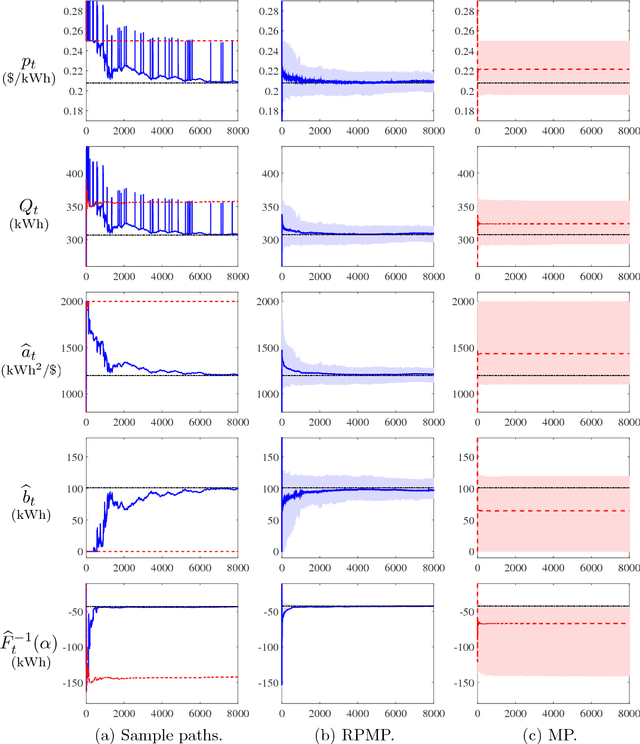
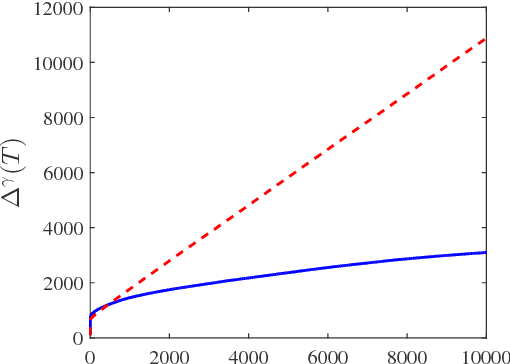
We adopt the perspective of an aggregator, which seeks to coordinate its purchase of demand reductions from a fixed group of residential electricity customers, with its sale of the aggregate demand reduction in a two-settlement wholesale energy market. The aggregator procures reductions in demand by offering its customers a uniform price for reductions in consumption relative to their predetermined baselines. Prior to its realization of the aggregate demand reduction, the aggregator must also determine how much energy to sell into the two-settlement energy market. In the day-ahead market, the aggregator commits to a forward contract, which calls for the delivery of energy in the real-time market. The underlying aggregate demand curve, which relates the aggregate demand reduction to the aggregator's offered price, is assumed to be affine and subject to unobservable, random shocks. Assuming that both the parameters of the demand curve and the distribution of the random shocks are initially unknown to the aggregator, we investigate the extent to which the aggregator might dynamically adapt its offered prices and forward contracts to maximize its expected profit over a time window of $T$ days. Specifically, we design a dynamic pricing and contract offering policy that resolves the aggregator's need to learn the unknown demand model with its desire to maximize its cumulative expected profit over time. In particular, the proposed pricing policy is proven to incur a regret over $T$ days that is no greater than $O(\log(T)\sqrt{T})$.