An Online Learning Approach to Buying and Selling Demand Response
Paper and Code
Dec 28, 2017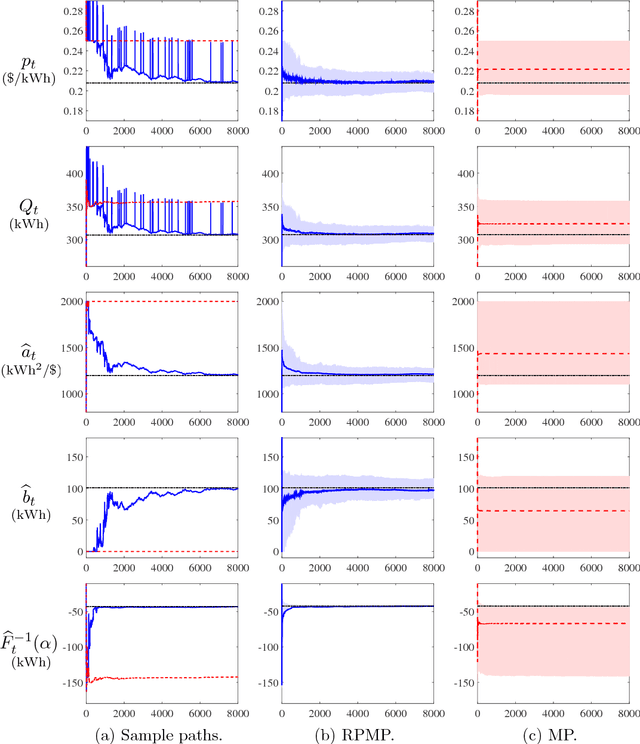
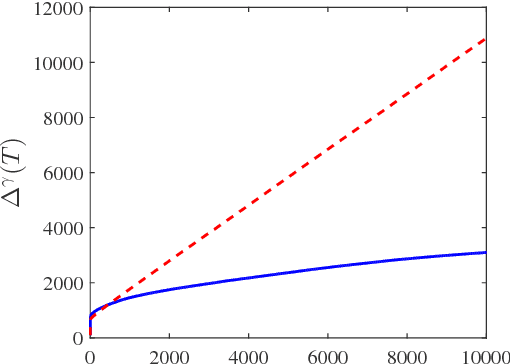
We adopt the perspective of an aggregator, which seeks to coordinate its purchase of demand reductions from a fixed group of residential electricity customers, with its sale of the aggregate demand reduction in a two-settlement wholesale energy market. The aggregator procures reductions in demand by offering its customers a uniform price for reductions in consumption relative to their predetermined baselines. Prior to its realization of the aggregate demand reduction, the aggregator must also determine how much energy to sell into the two-settlement energy market. In the day-ahead market, the aggregator commits to a forward contract, which calls for the delivery of energy in the real-time market. The underlying aggregate demand curve, which relates the aggregate demand reduction to the aggregator's offered price, is assumed to be affine and subject to unobservable, random shocks. Assuming that both the parameters of the demand curve and the distribution of the random shocks are initially unknown to the aggregator, we investigate the extent to which the aggregator might dynamically adapt its offered prices and forward contracts to maximize its expected profit over a time window of $T$ days. Specifically, we design a dynamic pricing and contract offering policy that resolves the aggregator's need to learn the unknown demand model with its desire to maximize its cumulative expected profit over time. In particular, the proposed pricing policy is proven to incur a regret over $T$ days that is no greater than $O(\log(T)\sqrt{T})$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge