Predicting Nearly As Well As the Optimal Twice Differentiable Regressor

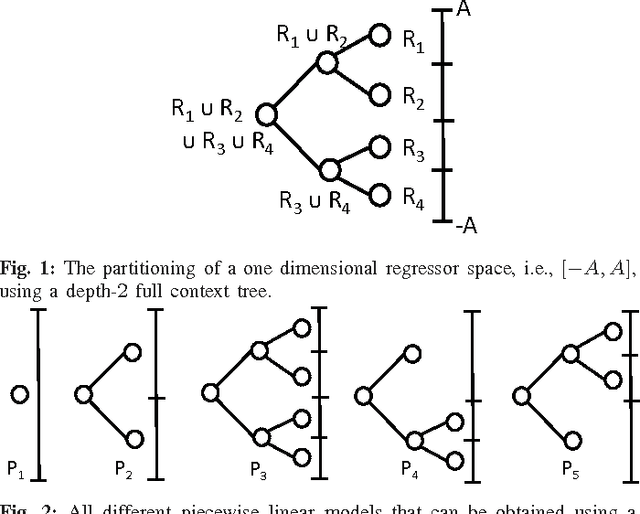
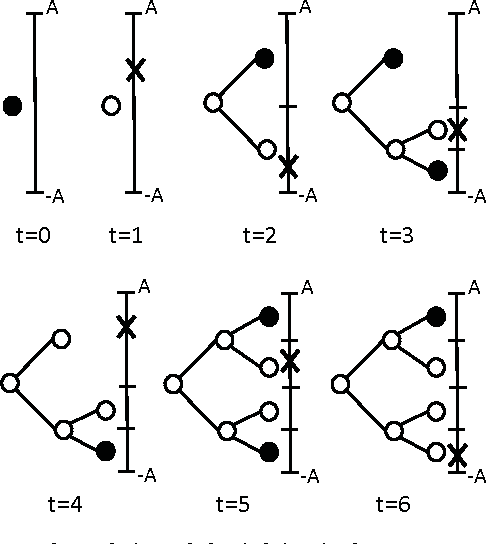
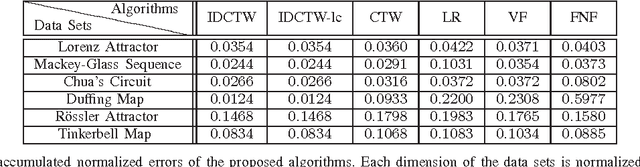
We study nonlinear regression of real valued data in an individual sequence manner, where we provide results that are guaranteed to hold without any statistical assumptions. We address the convergence and undertraining issues of conventional nonlinear regression methods and introduce an algorithm that elegantly mitigates these issues via an incremental hierarchical structure, (i.e., via an incremental decision tree). Particularly, we present a piecewise linear (or nonlinear) regression algorithm that partitions the regressor space in a data driven manner and learns a linear model at each region. Unlike the conventional approaches, our algorithm gradually increases the number of disjoint partitions on the regressor space in a sequential manner according to the observed data. Through this data driven approach, our algorithm sequentially and asymptotically achieves the performance of the optimal twice differentiable regression function for any data sequence with an unknown and arbitrary length. The computational complexity of the introduced algorithm is only logarithmic in the data length under certain regularity conditions. We provide the explicit description of the algorithm and demonstrate the significant gains for the well-known benchmark real data sets and chaotic signals.