Predicting Nearly As Well As the Optimal Twice Differentiable Regressor

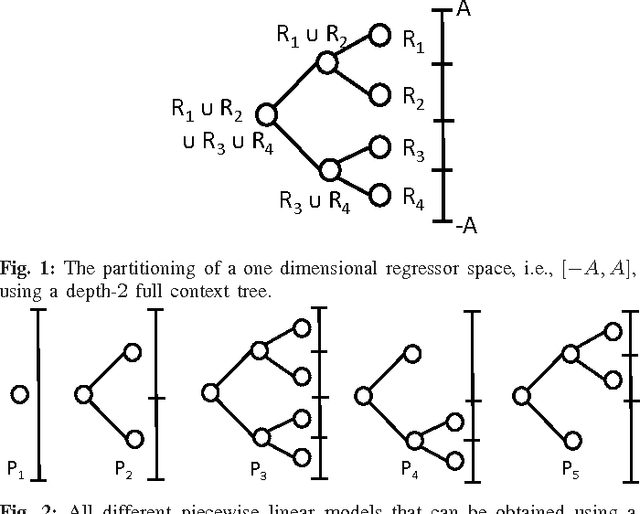
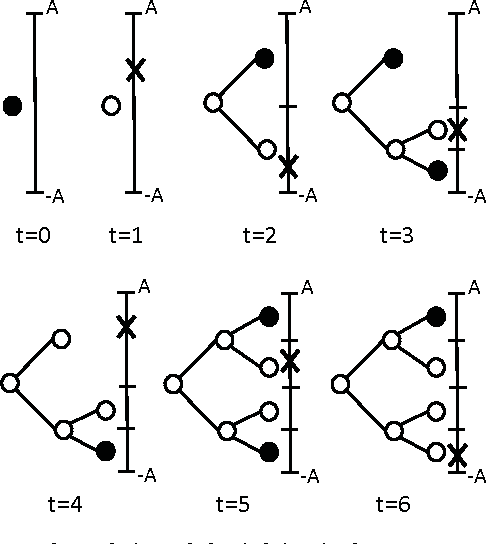
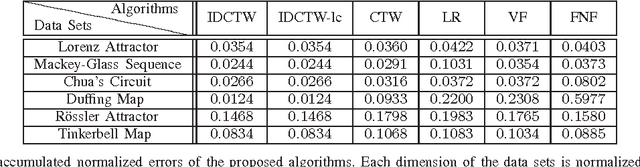
We study nonlinear regression of real valued data in an individual sequence manner, where we provide results that are guaranteed to hold without any statistical assumptions. We address the convergence and undertraining issues of conventional nonlinear regression methods and introduce an algorithm that elegantly mitigates these issues via an incremental hierarchical structure, (i.e., via an incremental decision tree). Particularly, we present a piecewise linear (or nonlinear) regression algorithm that partitions the regressor space in a data driven manner and learns a linear model at each region. Unlike the conventional approaches, our algorithm gradually increases the number of disjoint partitions on the regressor space in a sequential manner according to the observed data. Through this data driven approach, our algorithm sequentially and asymptotically achieves the performance of the optimal twice differentiable regression function for any data sequence with an unknown and arbitrary length. The computational complexity of the introduced algorithm is only logarithmic in the data length under certain regularity conditions. We provide the explicit description of the algorithm and demonstrate the significant gains for the well-known benchmark real data sets and chaotic signals.

A Unified Approach to Universal Prediction: Generalized Upper and Lower Bounds

We study sequential prediction of real-valued, arbitrary and unknown sequences under the squared error loss as well as the best parametric predictor out of a large, continuous class of predictors. Inspired by recent results from computational learning theory, we refrain from any statistical assumptions and define the performance with respect to the class of general parametric predictors. In particular, we present generic lower and upper bounds on this relative performance by transforming the prediction task into a parameter learning problem. We first introduce the lower bounds on this relative performance in the mixture of experts framework, where we show that for any sequential algorithm, there always exists a sequence for which the performance of the sequential algorithm is lower bounded by zero. We then introduce a sequential learning algorithm to predict such arbitrary and unknown sequences, and calculate upper bounds on its total squared prediction error for every bounded sequence. We further show that in some scenarios we achieve matching lower and upper bounds demonstrating that our algorithms are optimal in a strong minimax sense such that their performances cannot be improved further. As an interesting result we also prove that for the worst case scenario, the performance of randomized algorithms can be achieved by sequential algorithms so that randomized algorithms does not improve the performance.

A Comprehensive Approach to Universal Piecewise Nonlinear Regression Based on Trees

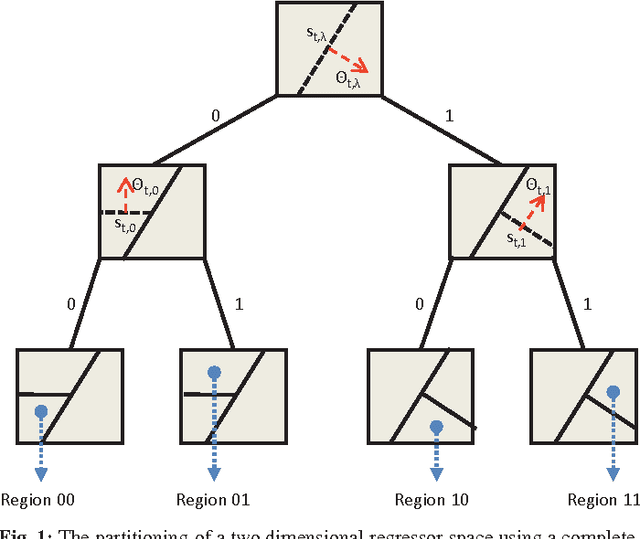
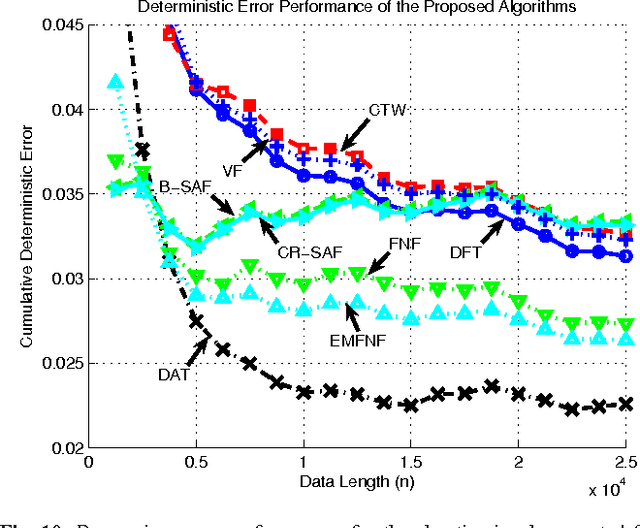
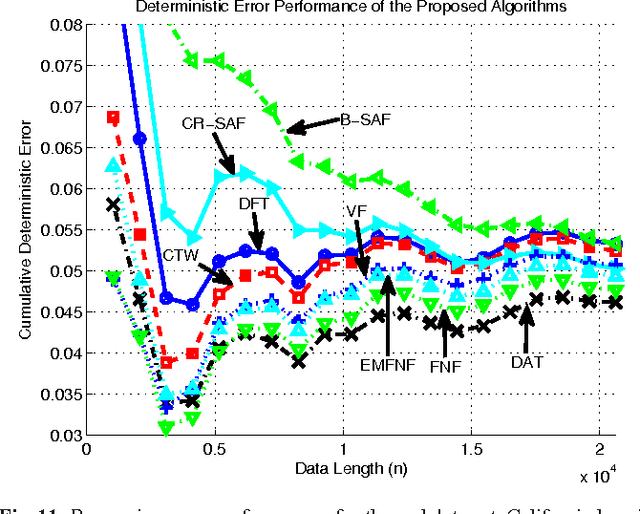
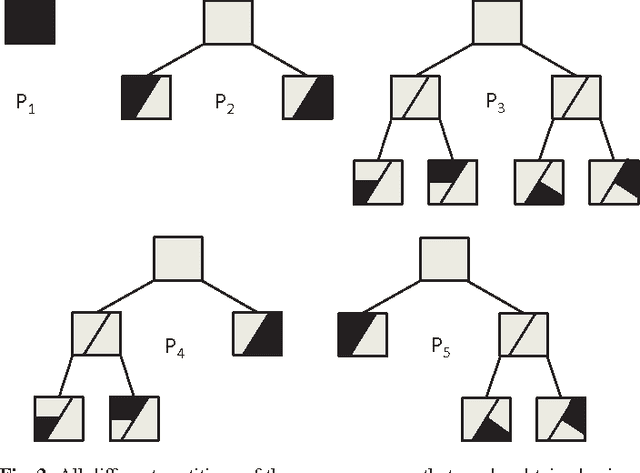
In this paper, we investigate adaptive nonlinear regression and introduce tree based piecewise linear regression algorithms that are highly efficient and provide significantly improved performance with guaranteed upper bounds in an individual sequence manner. We use a tree notion in order to partition the space of regressors in a nested structure. The introduced algorithms adapt not only their regression functions but also the complete tree structure while achieving the performance of the "best" linear mixture of a doubly exponential number of partitions, with a computational complexity only polynomial in the number of nodes of the tree. While constructing these algorithms, we also avoid using any artificial "weighting" of models (with highly data dependent parameters) and, instead, directly minimize the final regression error, which is the ultimate performance goal. The introduced methods are generic such that they can readily incorporate different tree construction methods such as random trees in their framework and can use different regressor or partitioning functions as demonstrated in the paper.

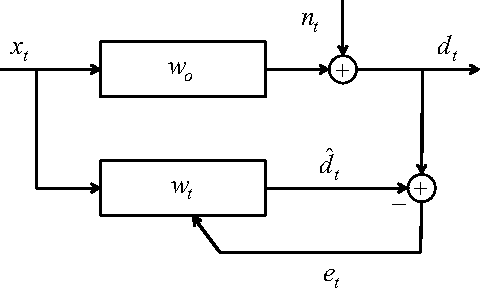
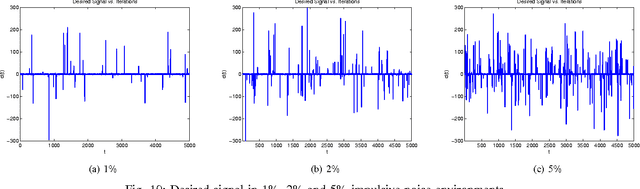
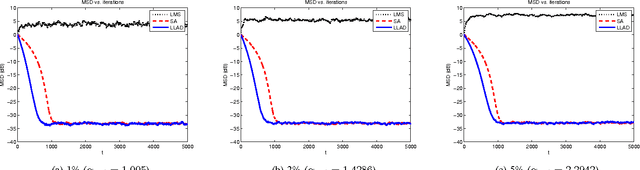
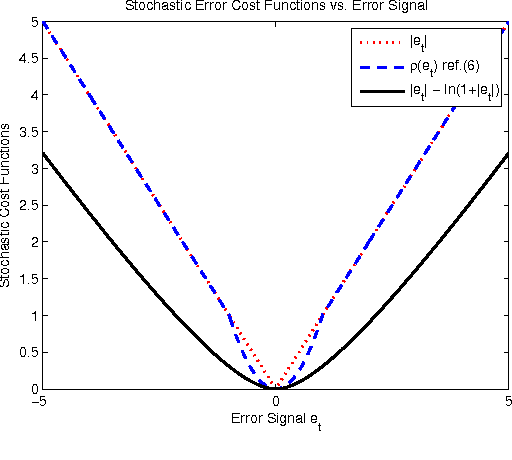
A Novel Family of Adaptive Filtering Algorithms Based on The Logarithmic Cost

We introduce a novel family of adaptive filtering algorithms based on a relative logarithmic cost. The new family intrinsically combines the higher and lower order measures of the error into a single continuous update based on the error amount. We introduce important members of this family of algorithms such as the least mean logarithmic square (LMLS) and least logarithmic absolute difference (LLAD) algorithms that improve the convergence performance of the conventional algorithms. However, our approach and analysis are generic such that they cover other well-known cost functions as described in the paper. The LMLS algorithm achieves comparable convergence performance with the least mean fourth (LMF) algorithm and extends the stability bound on the step size. The LLAD and least mean square (LMS) algorithms demonstrate similar convergence performance in impulse-free noise environments while the LLAD algorithm is robust against impulsive interferences and outperforms the sign algorithm (SA). We analyze the transient, steady state and tracking performance of the introduced algorithms and demonstrate the match of the theoretical analyzes and simulation results. We show the extended stability bound of the LMLS algorithm and analyze the robustness of the LLAD algorithm against impulsive interferences. Finally, we demonstrate the performance of our algorithms in different scenarios through numerical examples.