A Novel Family of Adaptive Filtering Algorithms Based on The Logarithmic Cost

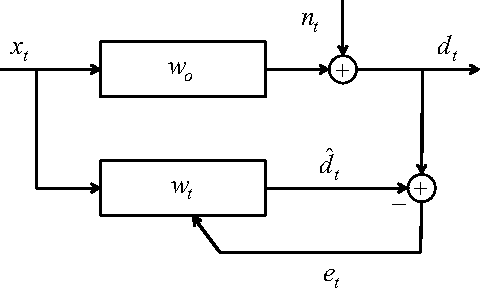
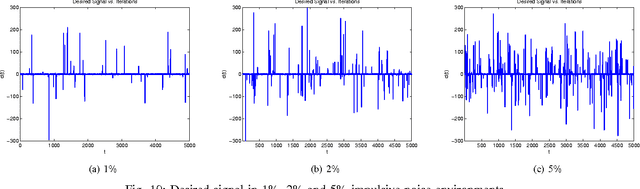
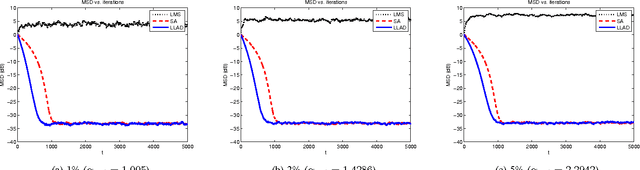
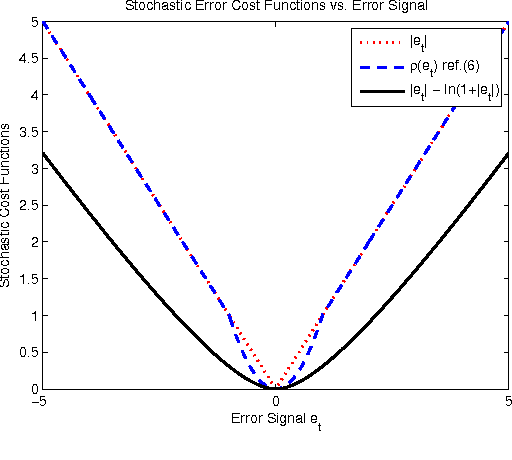
We introduce a novel family of adaptive filtering algorithms based on a relative logarithmic cost. The new family intrinsically combines the higher and lower order measures of the error into a single continuous update based on the error amount. We introduce important members of this family of algorithms such as the least mean logarithmic square (LMLS) and least logarithmic absolute difference (LLAD) algorithms that improve the convergence performance of the conventional algorithms. However, our approach and analysis are generic such that they cover other well-known cost functions as described in the paper. The LMLS algorithm achieves comparable convergence performance with the least mean fourth (LMF) algorithm and extends the stability bound on the step size. The LLAD and least mean square (LMS) algorithms demonstrate similar convergence performance in impulse-free noise environments while the LLAD algorithm is robust against impulsive interferences and outperforms the sign algorithm (SA). We analyze the transient, steady state and tracking performance of the introduced algorithms and demonstrate the match of the theoretical analyzes and simulation results. We show the extended stability bound of the LMLS algorithm and analyze the robustness of the LLAD algorithm against impulsive interferences. Finally, we demonstrate the performance of our algorithms in different scenarios through numerical examples.