Cognitive Insights and Stable Coalition Matching for Fostering Multi-Agent Cooperation

Cognitive abilities, such as Theory of Mind (ToM), play a vital role in facilitating cooperation in human social interactions. However, our study reveals that agents with higher ToM abilities may not necessarily exhibit better cooperative behavior compared to those with lower ToM abilities. To address this challenge, we propose a novel matching coalition mechanism that leverages the strengths of agents with different ToM levels by explicitly considering belief alignment and specialized abilities when forming coalitions. Our proposed matching algorithm seeks to find stable coalitions that maximize the potential for cooperative behavior and ensure long-term viability. By incorporating cognitive insights into the design of multi-agent systems, our work demonstrates the potential of leveraging ToM to create more sophisticated and human-like coordination strategies that foster cooperation and improve overall system performance.

Federated Learning With Energy Harvesting Devices: An MDP Framework

Federated learning (FL) requires edge devices to perform local training and exchange information with a parameter server, leading to substantial energy consumption. A critical challenge in practical FL systems is the rapid energy depletion of battery-limited edge devices, which curtails their operational lifespan and affects the learning performance. To address this issue, we apply energy harvesting technique in FL systems to extract ambient energy for continuously powering edge devices. We first establish the convergence bound for the wireless FL system with energy harvesting devices, illustrating that the convergence is impacted by partial device participation and packet drops, both of which depend on the energy supply. To accelerate the convergence, we formulate a joint device scheduling and power control problem and model it as a Markov decision process (MDP). By solving this MDP, we derive the optimal transmission policy and demonstrate that it possesses a monotone structure with respect to the battery and channel states. To overcome the curse of dimensionality caused by the exponential complexity of computing the optimal policy, we propose a low-complexity algorithm, which is asymptotically optimal as the number of devices increases. Furthermore, for unknown channels and harvested energy statistics, we develop a structure-enhanced deep reinforcement learning algorithm that leverages the monotone structure of the optimal policy to improve the training performance. Finally, extensive numerical experiments on real-world datasets are presented to validate the theoretical results and corroborate the effectiveness of the proposed algorithms.

Federated Unlearning: a Perspective of Stability and Fairness

This paper explores the multifaceted consequences of federated unlearning (FU) with data heterogeneity. We introduce key metrics for FU assessment, concentrating on verification, global stability, and local fairness, and investigate the inherent trade-offs. Furthermore, we formulate the unlearning process with data heterogeneity through an optimization framework. Our key contribution lies in a comprehensive theoretical analysis of the trade-offs in FU and provides insights into data heterogeneity's impacts on FU. Leveraging these insights, we propose FU mechanisms to manage the trade-offs, guiding further development for FU mechanisms. We empirically validate that our FU mechanisms effectively balance trade-offs, confirming insights derived from our theoretical analysis.

Decentralized Multi-Task Online Convex Optimization Under Random Link Failures

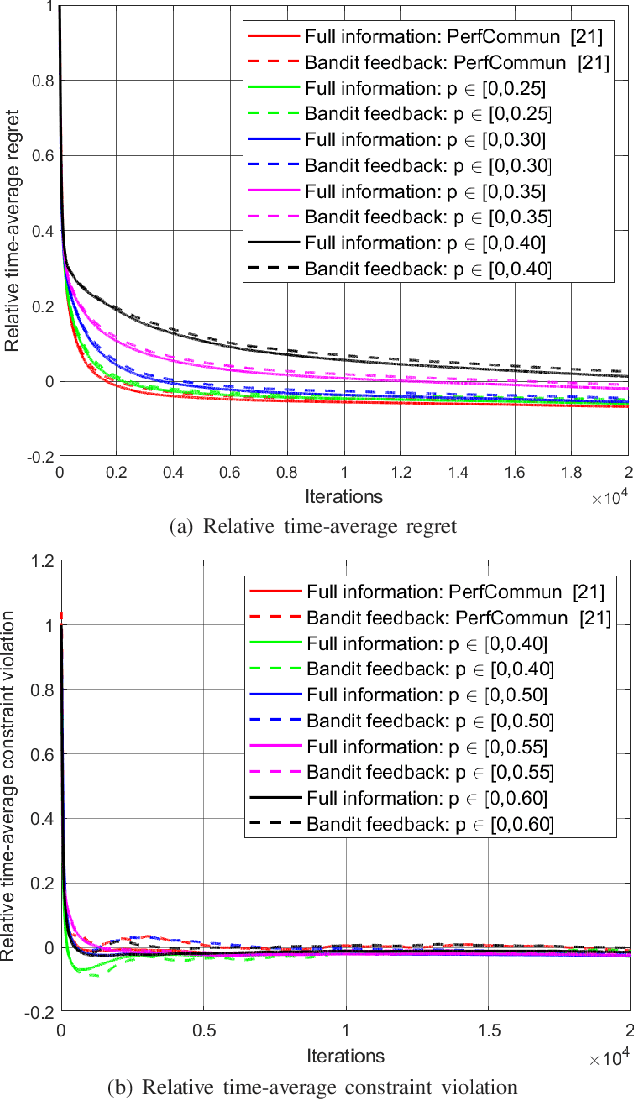
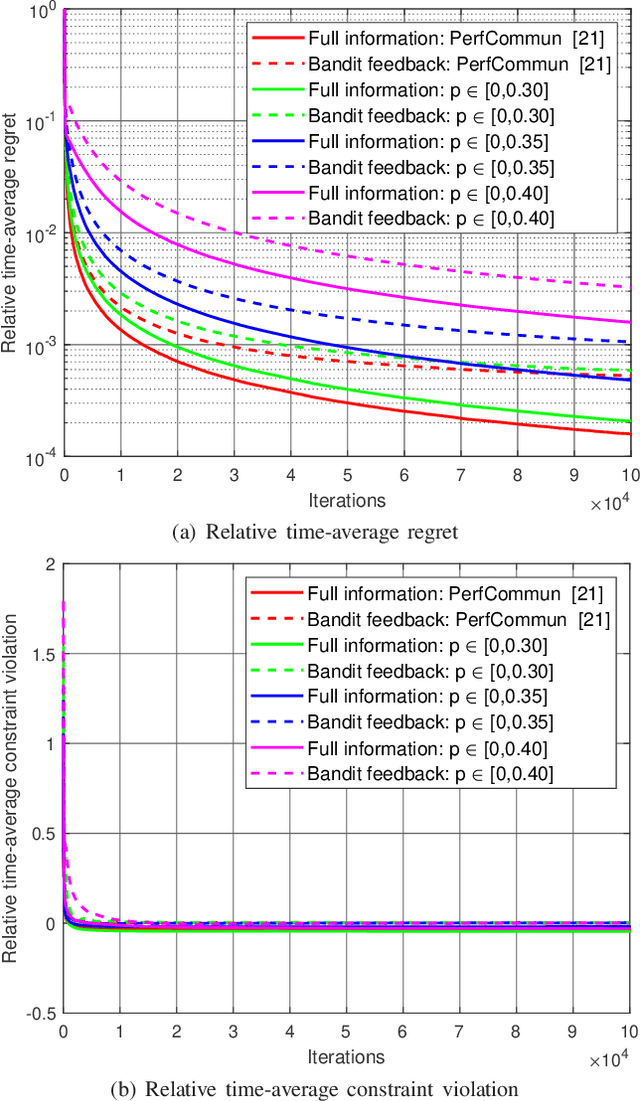
Decentralized optimization methods often entail information exchange between neighbors. Transmission failures can happen due to network congestion, hardware/software issues, communication outage, and other factors. In this paper, we investigate the random link failure problem in decentralized multi-task online convex optimization, where agents have individual decisions that are coupled with each other via pairwise constraints. Although widely used in constrained optimization, conventional saddle-point algorithms are not directly applicable here because of random packet dropping. To address this issue, we develop a robust decentralized saddle-point algorithm against random link failures with heterogeneous probabilities by replacing the missing decisions of neighbors with their latest received values. Then, by judiciously bounding the accumulated deviation stemming from this replacement, we first establish that our algorithm achieves $\mathcal{O}(\sqrt{T})$ regret and $\mathcal{O}(T^\frac{3}{4})$ constraint violations for the full information scenario, where the complete information on the local cost function is revealed to each agent at the end of each time slot. These two bounds match, in order sense, the performance bounds of algorithms with perfect communications. Further, we extend our algorithm and analysis to the two-point bandit feedback scenario, where only the values of the local cost function at two random points are disclosed to each agent sequentially. Performance bounds of the same orders as the full information case are derived. Finally, we corroborate the efficacy of the proposed algorithms and the analytical results through numerical simulations.

Zero-Regret Performative Prediction Under Inequality Constraints

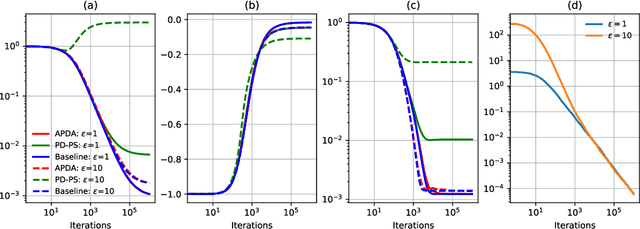
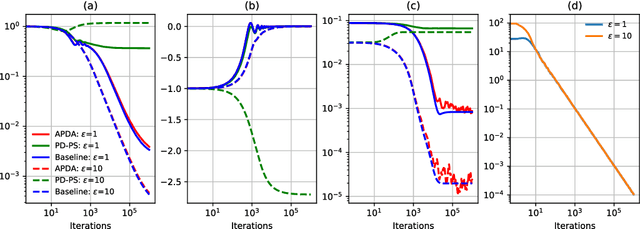
Performative prediction is a recently proposed framework where predictions guide decision-making and hence influence future data distributions. Such performative phenomena are ubiquitous in various areas, such as transportation, finance, public policy, and recommendation systems. To date, work on performative prediction has only focused on unconstrained scenarios, neglecting the fact that many real-world learning problems are subject to constraints. This paper bridges this gap by studying performative prediction under inequality constraints. Unlike most existing work that provides only performative stable points, we aim to find the optimal solutions. Anticipating performative gradients is a challenging task, due to the agnostic performative effect on data distributions. To address this issue, we first develop a robust primal-dual framework that requires only approximate gradients up to a certain accuracy, yet delivers the same order of performance as the stochastic primal-dual algorithm without performativity. Based on this framework, we then propose an adaptive primal-dual algorithm for location families. Our analysis demonstrates that the proposed adaptive primal-dual algorithm attains $\ca{O}(\sqrt{T})$ regret and constraint violations, using only $\sqrt{T} + 2T$ samples, where $T$ is the time horizon. To our best knowledge, this is the first study and analysis on the optimality of the performative prediction problem under inequality constraints. Finally, we validate the effectiveness of our algorithm and theoretical results through numerical simulations.

Decentralized Multi-Task Stochastic Optimization With Compressed Communications

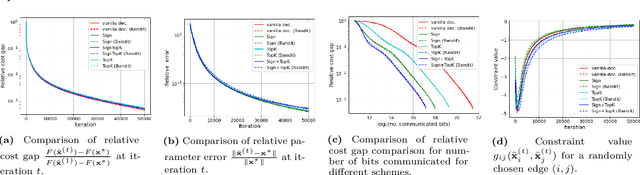
We consider a multi-agent network where each node has a stochastic (local) cost function that depends on the decision variable of that node and a random variable, and further the decision variables of neighboring nodes are pairwise constrained. There is an aggregate objective function for the network, composed additively of the expected values of the local cost functions at the nodes, and the overall goal of the network is to obtain the minimizing solution to this aggregate objective function subject to all the pairwise constraints. This is to be achieved at the node level using decentralized information and local computation, with exchanges of only compressed information allowed by neighboring nodes. The paper develops algorithms and obtains performance bounds for two different models of local information availability at the nodes: (i) sample feedback, where each node has direct access to samples of the local random variable to evaluate its local cost, and (ii) bandit feedback, where samples of the random variables are not available, but only the values of the local cost functions at two random points close to the decision are available to each node. For both models, with compressed communication between neighbors, we have developed decentralized saddle-point algorithms that deliver performances no different (in order sense) from those without communication compression; specifically, we show that deviation from the global minimum value and violations of the constraints are upper-bounded by $\mathcal{O}(T^{-\frac{1}{2}})$ and $\mathcal{O}(T^{-\frac{1}{4}})$, respectively, where $T$ is the number of iterations. Numerical examples provided in the paper corroborate these bounds and demonstrate the communication efficiency of the proposed method.