Stochastic Games for Smart Grid Energy Management with Prospect Prosumers

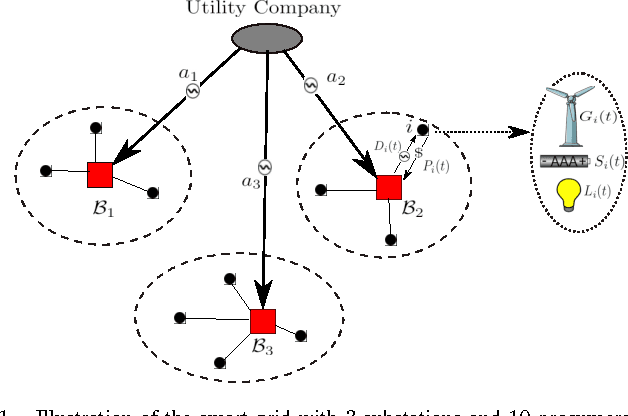
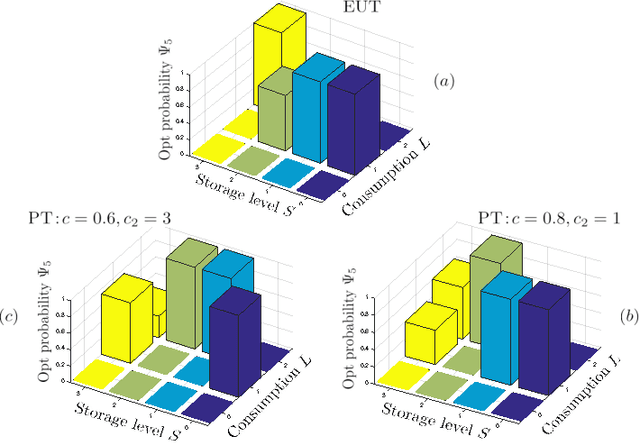
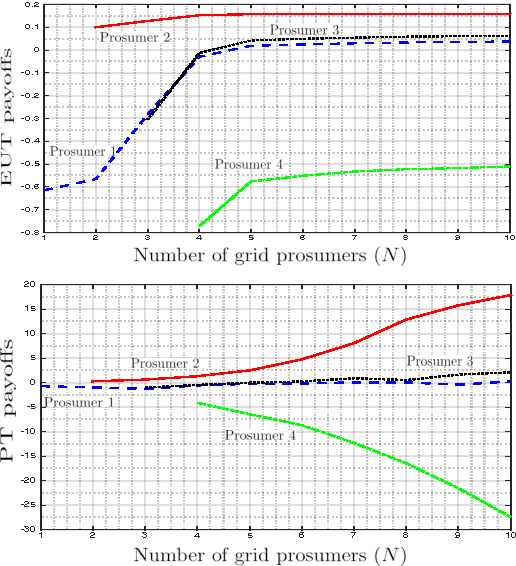
In this paper, the problem of smart grid energy management under stochastic dynamics is investigated. In the considered model, at the demand side, it is assumed that customers can act as prosumers who own renewable energy sources and can both produce and consume energy. Due to the coupling between the prosumers' decisions and the stochastic nature of renewable energy, the interaction among prosumers is formulated as a stochastic game, in which each prosumer seeks to maximize its payoff, in terms of revenues, by controlling its energy consumption and demand. In particular, the subjective behavior of prosumers is explicitly reflected into their payoff functions using prospect theory, a powerful framework that allows modeling real-life human choices. For this prospect-based stochastic game, it is shown that there always exists a stationary Nash equilibrium where the prosumers' trading policies in the equilibrium are independent of the time and their histories of the play. Moreover, a novel distributed algorithm with no information sharing among prosumers is proposed and shown to converge to an $\epsilon$-Nash equilibrium. On the other hand, at the supply side, the interaction between the utility company and the prosumers is formulated as an online optimization problem in which the utility company's goal is to learn its optimal energy allocation rules. For this case, it is shown that such an optimization problem admits a no-regret algorithm meaning that regardless of the actual outcome of the game among the prosumers, the utility company can follow a strategy that mitigates its allocation costs as if it knew the entire demand market a priori. Simulation results show the convergence of the proposed algorithms to their predicted outcomes and present new insights resulting from prospect theory that contribute toward more efficient energy management in the smart grids.

Game-Theoretic Analysis of the Hegselmann-Krause Model for Opinion Dynamics in Finite Dimensions

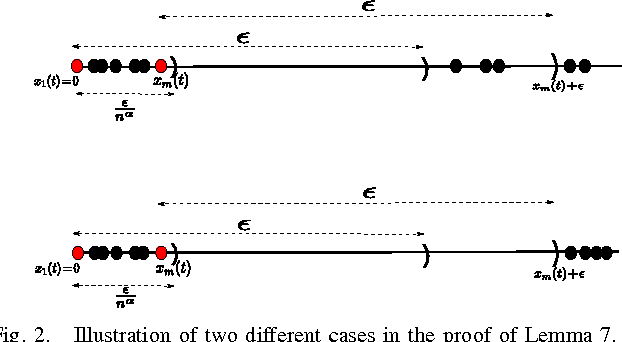
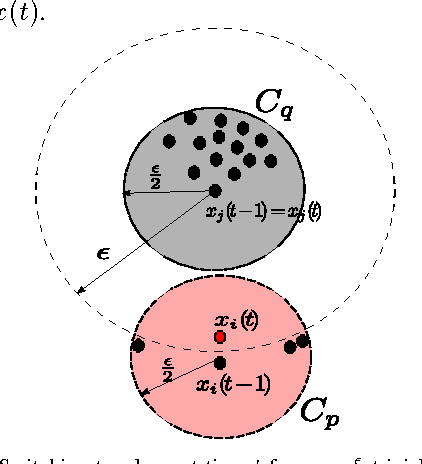
We consider the Hegselmann-Krause model for opinion dynamics and study the evolution of the system under various settings. We first analyze the termination time of the synchronous Hegselmann-Krause dynamics in arbitrary finite dimensions and show that the termination time in general only depends on the number of agents involved in the dynamics. To the best of our knowledge, that is the sharpest bound for the termination time of such dynamics that removes dependency of the termination time from the dimension of the ambient space. This answers an open question in [1] on how to obtain a tighter upper bound for the termination time. Furthermore, we study the asynchronous Hegselmann-Krause model from a novel game-theoretic approach and show that the evolution of an asynchronous Hegselmann-Krause model is equivalent to a sequence of best response updates in a well-designed potential game. We then provide a polynomial upper bound for the expected time and expected number of switching topologies until the dynamic reaches an arbitrarily small neighborhood of its equilibrium points, provided that the agents update uniformly at random. This is a step toward analysis of heterogeneous Hegselmann-Krause dynamics. Finally, we consider the heterogeneous Hegselmann-Krause dynamics and provide a necessary condition for the finite termination time of such dynamics. In particular, we sketch some future directions toward more detailed analysis of the heterogeneous Hegselmann-Krause model.