Decentralized Nonconvex Optimization with Guaranteed Privacy and Accuracy
Paper and Code
Dec 14, 2022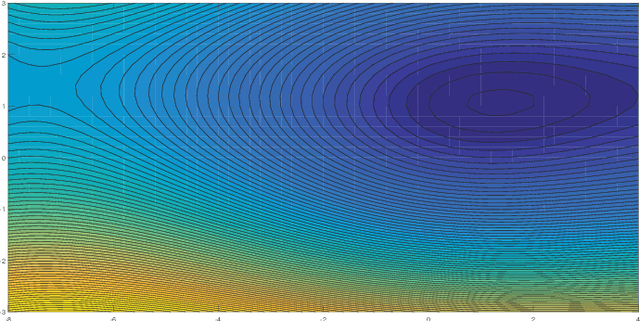
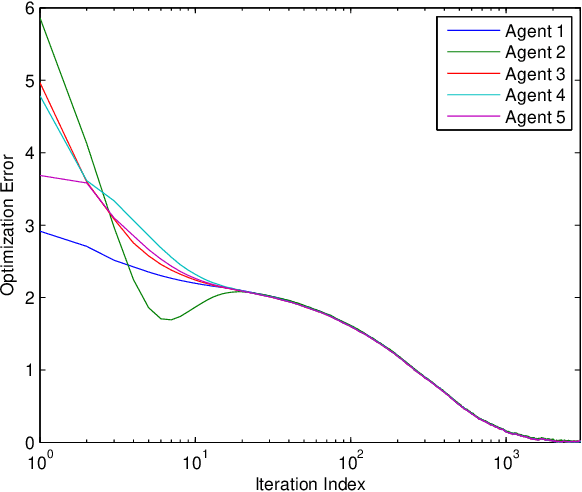
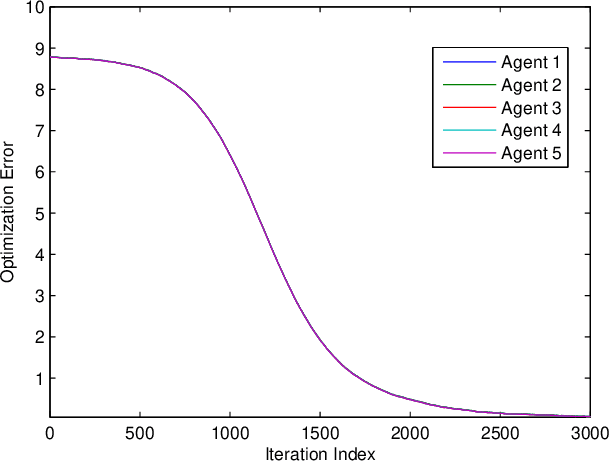
Privacy protection and nonconvexity are two challenging problems in decentralized optimization and learning involving sensitive data. Despite some recent advances addressing each of the two problems separately, no results have been reported that have theoretical guarantees on both privacy protection and saddle/maximum avoidance in decentralized nonconvex optimization. We propose a new algorithm for decentralized nonconvex optimization that can enable both rigorous differential privacy and saddle/maximum avoiding performance. The new algorithm allows the incorporation of persistent additive noise to enable rigorous differential privacy for data samples, gradients, and intermediate optimization variables without losing provable convergence, and thus circumventing the dilemma of trading accuracy for privacy in differential privacy design. More interestingly, the algorithm is theoretically proven to be able to efficiently { guarantee accuracy by avoiding} convergence to local maxima and saddle points, which has not been reported before in the literature on decentralized nonconvex optimization. The algorithm is efficient in both communication (it only shares one variable in each iteration) and computation (it is encryption-free), and hence is promising for large-scale nonconvex optimization and learning involving high-dimensional optimization parameters. Numerical experiments for both a decentralized estimation problem and an Independent Component Analysis (ICA) problem confirm the effectiveness of the proposed approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge