High-Dimensional Performance Modeling via Tensor Completion

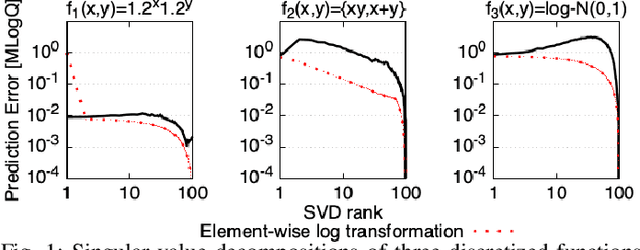
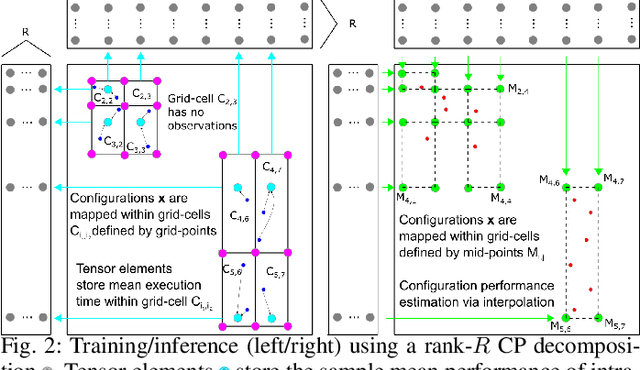
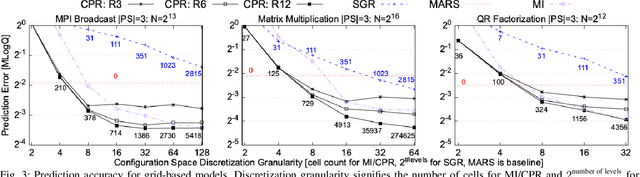
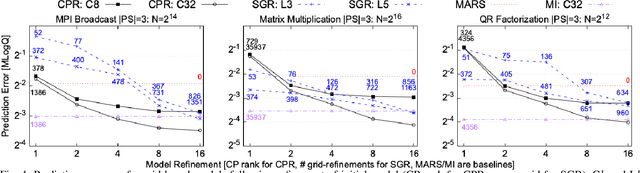
Performance tuning, software/hardware co-design, and job scheduling are among the many tasks that rely on models to predict application performance. We propose and evaluate low rank tensor decomposition for modeling application performance. We use tensors to represent regular grids that discretize the input and configuration domain of an application. Application execution times mapped within grid-cells are averaged and represented by tensor elements. We show that low-rank canonical-polyadic (CP) tensor decomposition is effective in approximating these tensors. We then employ tensor completion to optimize a CP decomposition given a sparse set of observed runtimes. We consider alternative piecewise/grid-based (P/G) and supervised learning models for six applications and demonstrate that P/G models are significantly more accurate relative to model size. Among P/G models, CP decomposition of regular grids (CPR) offers higher accuracy and memory-efficiency, faster optimization, and superior extensibility via user-selected loss functions and domain partitioning. CPR models achieve a 2.18x geometric mean decrease in mean prediction error relative to the most accurate alternative models of size $\le$10 kilobytes.

Cost-efficient Gaussian Tensor Network Embeddings for Tensor-structured Inputs

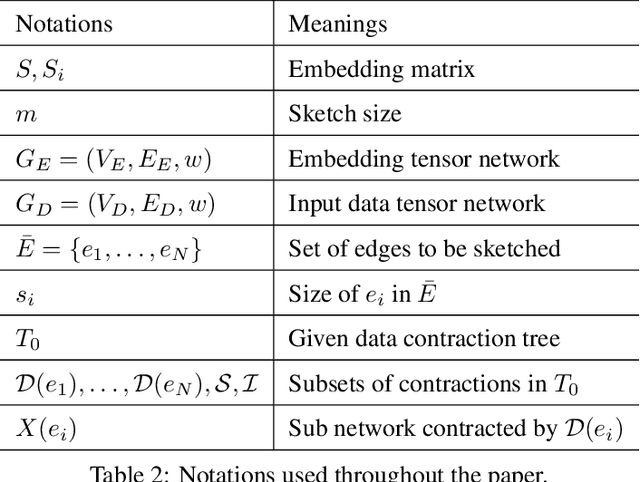
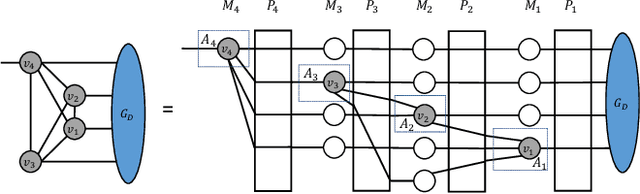
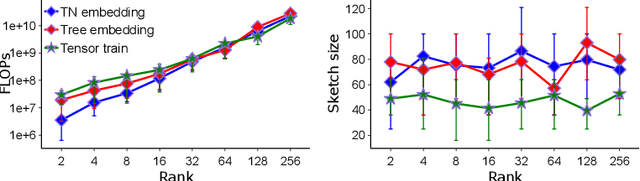
This work discusses tensor network embeddings, which are random matrices ($S$) with tensor network structure. These embeddings have been used to perform dimensionality reduction of tensor network structured inputs $x$ and accelerate applications such as tensor decomposition and kernel regression. Existing works have designed embeddings for inputs $x$ with specific structures, such that the computational cost for calculating $Sx$ is efficient. We provide a systematic way to design tensor network embeddings consisting of Gaussian random tensors, such that for inputs with more general tensor network structures, both the sketch size (row size of $S$) and the sketching computational cost are low. We analyze general tensor network embeddings that can be reduced to a sequence of sketching matrices. We provide a sufficient condition to quantify the accuracy of such embeddings and derive sketching asymptotic cost lower bounds using embeddings that satisfy this condition and have a sketch size lower than any input dimension. We then provide an algorithm to efficiently sketch input data using such embeddings. The sketch size of the embedding used in the algorithm has a linear dependence on the number of sketching dimensions of the input. Assuming tensor contractions are performed with classical dense matrix multiplication algorithms, this algorithm achieves asymptotic cost within a factor of $O(\sqrt{m})$ of our cost lower bound, where $m$ is the sketch size. Further, when each tensor in the input has a dimension that needs to be sketched, this algorithm yields the optimal sketching asymptotic cost. We apply our sketching analysis to inexact tensor decomposition optimization algorithms. We provide a sketching algorithm for CP decomposition that is asymptotically faster than existing work in multiple regimes, and show optimality of an existing algorithm for tensor train rounding.

Alternating Mahalanobis Distance Minimization for Stable and Accurate CP Decomposition

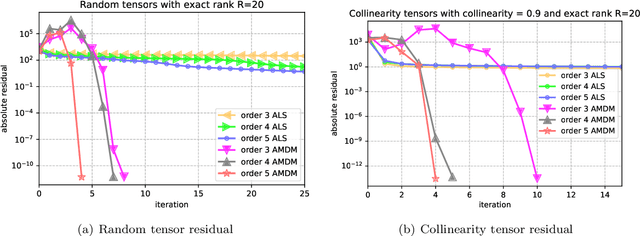
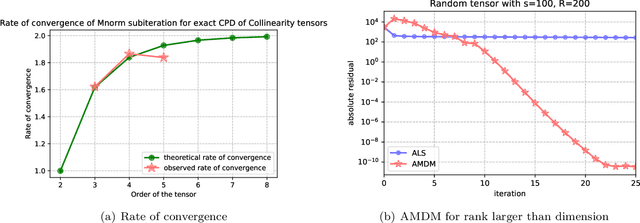
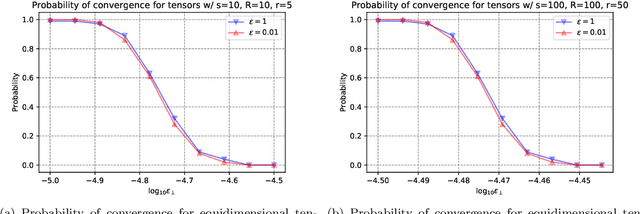
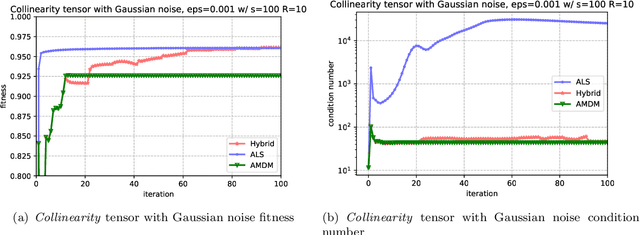
CP decomposition (CPD) is prevalent in chemometrics, signal processing, data mining and many more fields. While many algorithms have been proposed to compute the CPD, alternating least squares (ALS) remains one of the most widely used algorithm for computing the decomposition. Recent works have introduced the notion of eigenvalues and singular values of a tensor and explored applications of eigenvectors and singular vectors in areas like signal processing, data analytics and in various other fields. We introduce a new formulation for deriving singular values and vectors of a tensor by considering the critical points of a function different from what is used in the previous work. Computing these critical points in an alternating manner motivates an alternating optimization algorithm which corresponds to alternating least squares algorithm in the matrix case. However, for tensors with order greater than equal to $3$, it minimizes an objective function which is different from the commonly used least squares loss. Alternating optimization of this new objective leads to simple updates to the factor matrices with the same asymptotic computational cost as ALS. We show that a subsweep of this algorithm can achieve a superlinear convergence rate for exact CPD with known rank and verify it experimentally. We then view the algorithm as optimizing a Mahalanobis distance with respect to each factor with ground metric dependent on the other factors. This perspective allows us to generalize our approach to interpolate between updates corresponding to the ALS and the new algorithm to manage the tradeoff between stability and fitness of the decomposition. Our experimental results show that for approximating synthetic and real-world tensors, this algorithm and its variants converge to a better conditioned decomposition with comparable and sometimes better fitness as compared to the ALS algorithm.

Augmented Tensor Decomposition with Stochastic Optimization

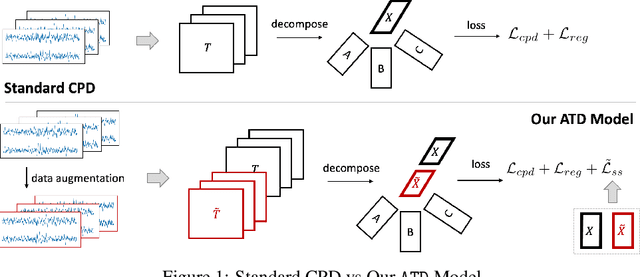
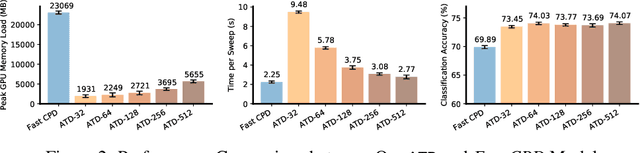
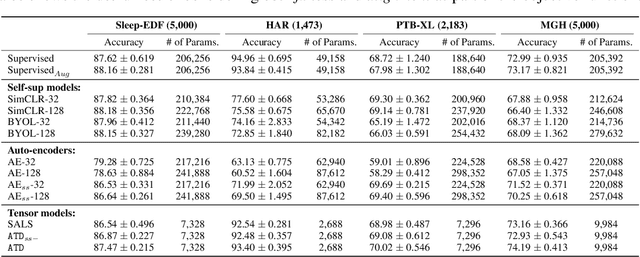
Tensor decompositions are powerful tools for dimensionality reduction and feature interpretation of multidimensional data such as signals. Existing tensor decomposition objectives (e.g., Frobenius norm) are designed for fitting raw data under statistical assumptions, which may not align with downstream classification tasks. Also, real-world tensor data are usually high-ordered and have large dimensions with millions or billions of entries. Thus, it is expensive to decompose the whole tensor with traditional algorithms. In practice, raw tensor data also contains redundant information while data augmentation techniques may be used to smooth out noise in samples. This paper addresses the above challenges by proposing augmented tensor decomposition (ATD), which effectively incorporates data augmentations to boost downstream classification. To reduce the memory footprint of the decomposition, we propose a stochastic algorithm that updates the factor matrices in a batch fashion. We evaluate ATD on multiple signal datasets. It shows comparable or better performance (e.g., up to 15% in accuracy) over self-supervised and autoencoder baselines with less than 5% of model parameters, achieves 0.6% ~ 1.3% accuracy gain over other tensor-based baselines, and reduces the memory footprint by 9X when compared to standard tensor decomposition algorithms.

MTC: Multiresolution Tensor Completion from Partial and Coarse Observations

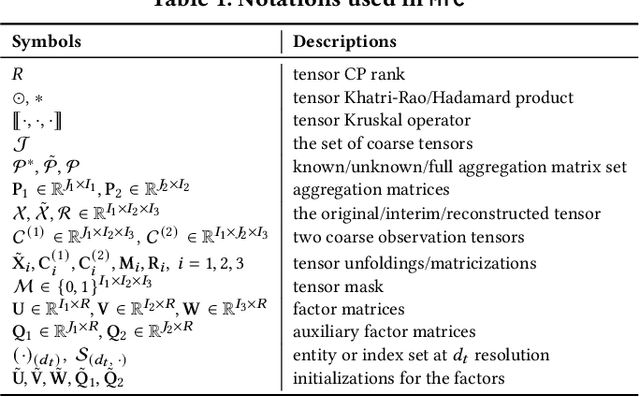
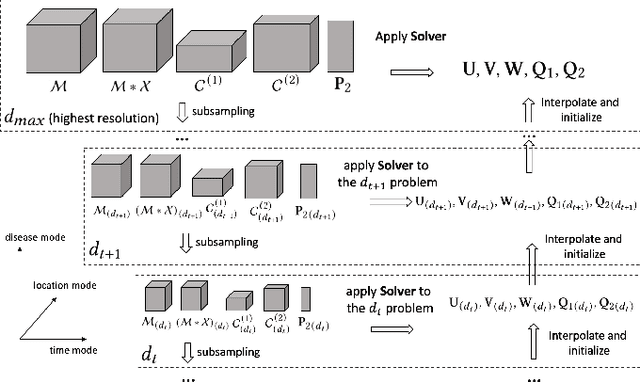
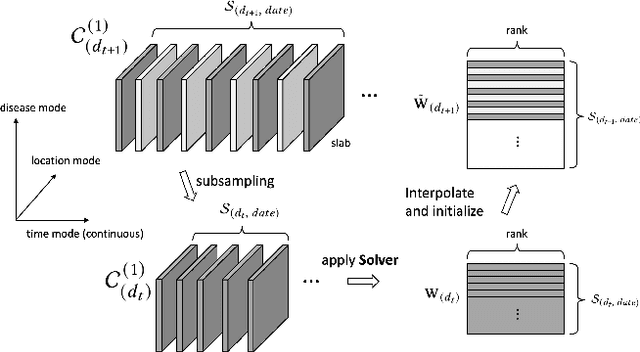
Existing tensor completion formulation mostly relies on partial observations from a single tensor. However, tensors extracted from real-world data are often more complex due to: (i) Partial observation: Only a small subset (e.g., 5%) of tensor elements are available. (ii) Coarse observation: Some tensor modes only present coarse and aggregated patterns (e.g., monthly summary instead of daily reports). In this paper, we are given a subset of the tensor and some aggregated/coarse observations (along one or more modes) and seek to recover the original fine-granular tensor with low-rank factorization. We formulate a coupled tensor completion problem and propose an efficient Multi-resolution Tensor Completion model (MTC) to solve the problem. Our MTC model explores tensor mode properties and leverages the hierarchy of resolutions to recursively initialize an optimization setup, and optimizes on the coupled system using alternating least squares. MTC ensures low computational and space complexity. We evaluate our model on two COVID-19 related spatio-temporal tensors. The experiments show that MTC could provide 65.20% and 75.79% percentage of fitness (PoF) in tensor completion with only 5% fine granular observations, which is 27.96% relative improvement over the best baseline. To evaluate the learned low-rank factors, we also design a tensor prediction task for daily and cumulative disease case predictions, where MTC achieves 50% in PoF and 30% relative improvements over the best baseline.

Fast and Accurate Randomized Algorithms for Low-rank Tensor Decompositions

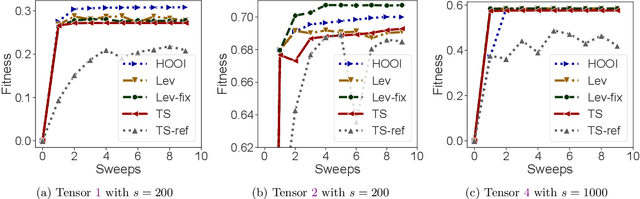
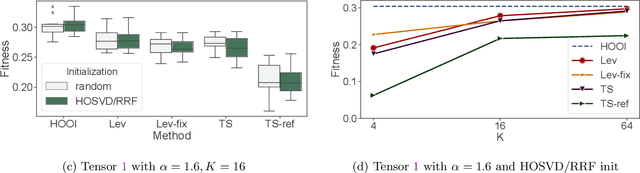
Low-rank Tucker and CP tensor decompositions are powerful tools in data analytics. The widely used alternating least squares (ALS) method, which solves a sequence of over-determined least squares subproblems, is inefficient for large and sparse tensors. We propose a fast and accurate sketched ALS algorithm for Tucker decomposition, which solves a sequence of sketched rank-constrained linear least squares subproblems. Theoretical sketch size upper bounds are provided to achieve $O(\epsilon)$-relative error for each subproblem with two sketching techniques, TensorSketch and leverage score sampling. Experimental results show that this new ALS algorithm, combined with a new initialization scheme based on randomized range finder, yields up to $22.0\%$ relative decomposition residual improvement compared to the state-of-the-art sketched randomized algorithm for Tucker decomposition of various synthetic datasets. This Tucker-ALS algorithm is further used to accelerate CP decomposition, by using randomized Tucker compression followed by CP decomposition of the Tucker core tensor. Experimental results show that this algorithm not only converges faster, but also yields more accurate CP decompositions.