High-Dimensional Performance Modeling via Tensor Completion

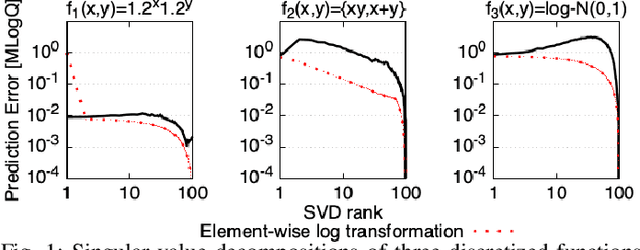
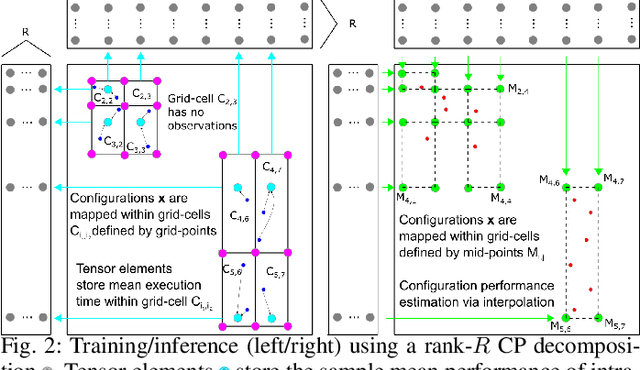
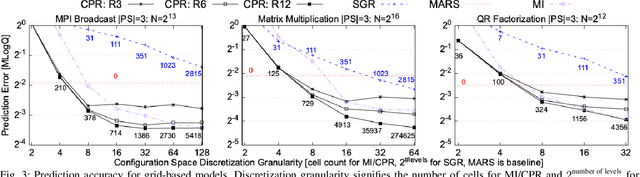
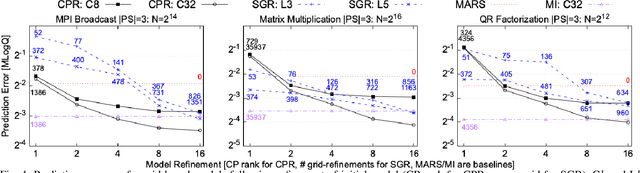
Performance tuning, software/hardware co-design, and job scheduling are among the many tasks that rely on models to predict application performance. We propose and evaluate low rank tensor decomposition for modeling application performance. We use tensors to represent regular grids that discretize the input and configuration domain of an application. Application execution times mapped within grid-cells are averaged and represented by tensor elements. We show that low-rank canonical-polyadic (CP) tensor decomposition is effective in approximating these tensors. We then employ tensor completion to optimize a CP decomposition given a sparse set of observed runtimes. We consider alternative piecewise/grid-based (P/G) and supervised learning models for six applications and demonstrate that P/G models are significantly more accurate relative to model size. Among P/G models, CP decomposition of regular grids (CPR) offers higher accuracy and memory-efficiency, faster optimization, and superior extensibility via user-selected loss functions and domain partitioning. CPR models achieve a 2.18x geometric mean decrease in mean prediction error relative to the most accurate alternative models of size $\le$10 kilobytes.