Leveraging the Human Ventral Visual Stream to Improve Neural Network Robustness

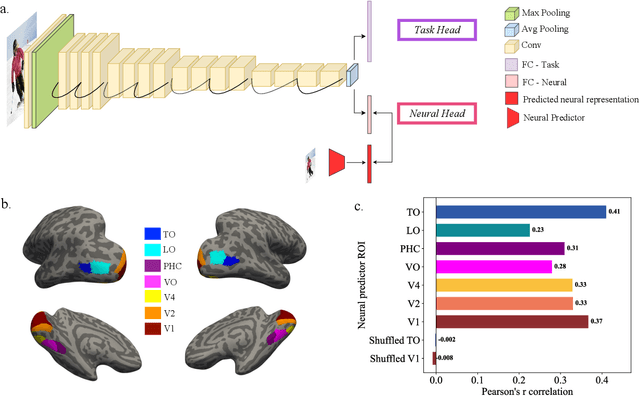
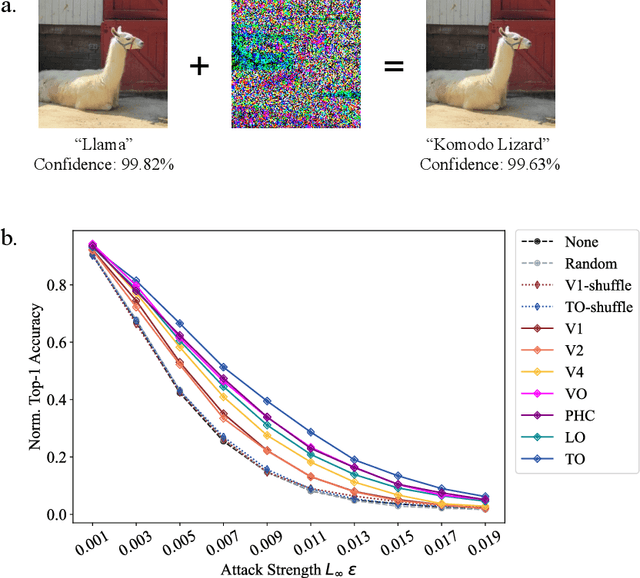
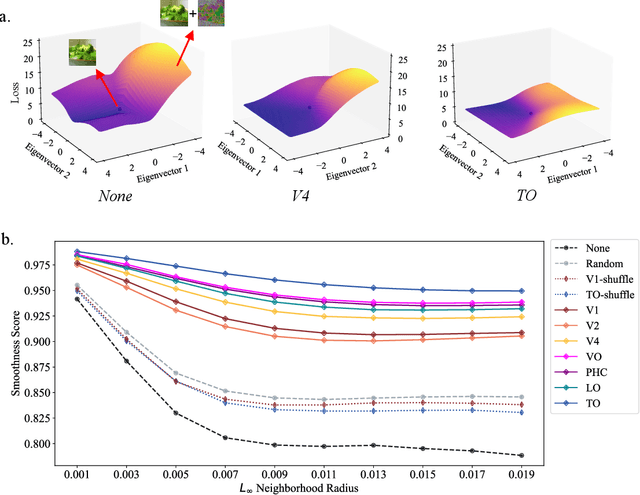
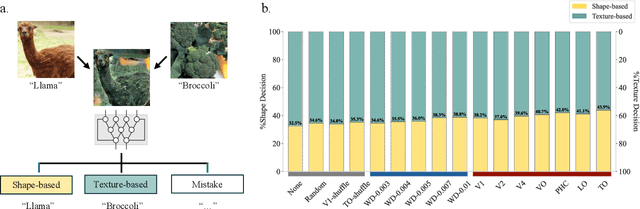
Human object recognition exhibits remarkable resilience in cluttered and dynamic visual environments. In contrast, despite their unparalleled performance across numerous visual tasks, Deep Neural Networks (DNNs) remain far less robust than humans, showing, for example, a surprising susceptibility to adversarial attacks involving image perturbations that are (almost) imperceptible to humans. Human object recognition likely owes its robustness, in part, to the increasingly resilient representations that emerge along the hierarchy of the ventral visual cortex. Here we show that DNNs, when guided by neural representations from a hierarchical sequence of regions in the human ventral visual stream, display increasing robustness to adversarial attacks. These neural-guided models also exhibit a gradual shift towards more human-like decision-making patterns and develop hierarchically smoother decision surfaces. Importantly, the resulting representational spaces differ in important ways from those produced by conventional smoothing methods, suggesting that such neural-guidance may provide previously unexplored robustness solutions. Our findings support the gradual emergence of human robustness along the ventral visual hierarchy and suggest that the key to DNN robustness may lie in increasing emulation of the human brain.

Cost-efficient Gaussian Tensor Network Embeddings for Tensor-structured Inputs

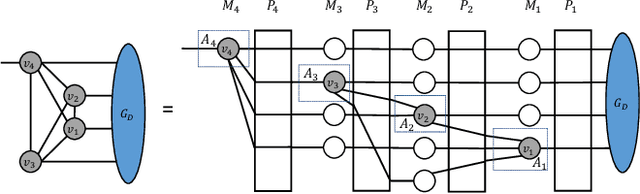
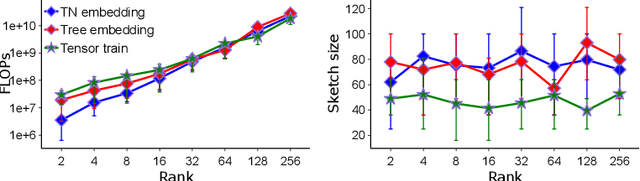
This work discusses tensor network embeddings, which are random matrices ($S$) with tensor network structure. These embeddings have been used to perform dimensionality reduction of tensor network structured inputs $x$ and accelerate applications such as tensor decomposition and kernel regression. Existing works have designed embeddings for inputs $x$ with specific structures, such that the computational cost for calculating $Sx$ is efficient. We provide a systematic way to design tensor network embeddings consisting of Gaussian random tensors, such that for inputs with more general tensor network structures, both the sketch size (row size of $S$) and the sketching computational cost are low. We analyze general tensor network embeddings that can be reduced to a sequence of sketching matrices. We provide a sufficient condition to quantify the accuracy of such embeddings and derive sketching asymptotic cost lower bounds using embeddings that satisfy this condition and have a sketch size lower than any input dimension. We then provide an algorithm to efficiently sketch input data using such embeddings. The sketch size of the embedding used in the algorithm has a linear dependence on the number of sketching dimensions of the input. Assuming tensor contractions are performed with classical dense matrix multiplication algorithms, this algorithm achieves asymptotic cost within a factor of $O(\sqrt{m})$ of our cost lower bound, where $m$ is the sketch size. Further, when each tensor in the input has a dimension that needs to be sketched, this algorithm yields the optimal sketching asymptotic cost. We apply our sketching analysis to inexact tensor decomposition optimization algorithms. We provide a sketching algorithm for CP decomposition that is asymptotically faster than existing work in multiple regimes, and show optimality of an existing algorithm for tensor train rounding.

MLPruning: A Multilevel Structured Pruning Framework for Transformer-based Models

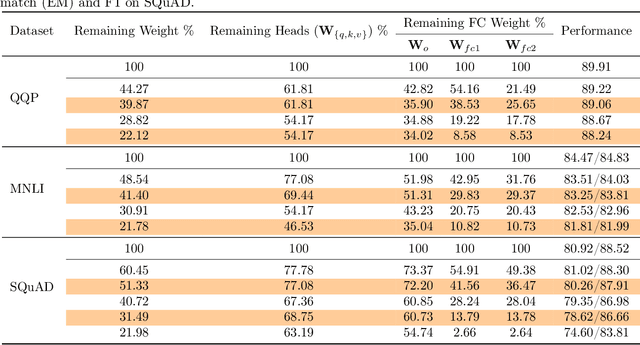
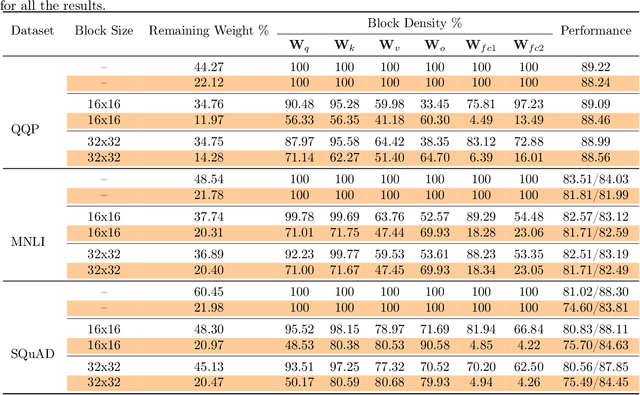
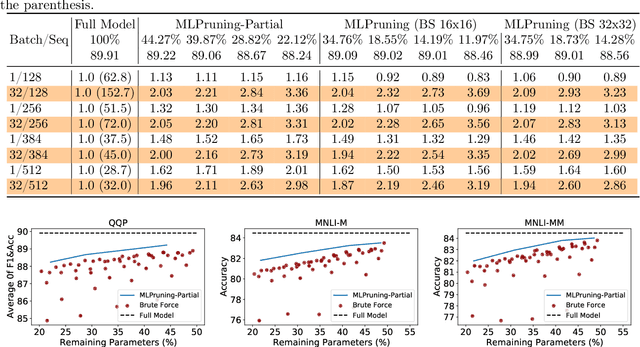
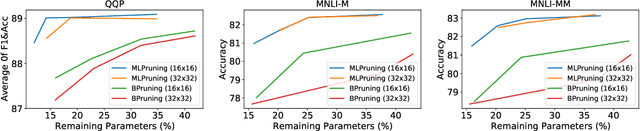
Pruning is an effective method to reduce the memory footprint and computational cost associated with large natural language processing models. However, current approaches either only explore head pruning, which has a limited pruning ratio, or only focus on unstructured pruning, which has negligible effects on the real inference time and/or power consumption. To address these challenges, we develop a novel MultiLevel structured Pruning (MLPruning) framework, which uses three different levels of structured pruning: head pruning, row pruning, and block-wise sparse pruning. We propose using a learnable Top-k threshold, which employs an adaptive regularization to adjust the regularization magnitude adaptively, to select appropriate pruning ratios for different weight matrices. We also propose a two-step pipeline to combine block-wise pruning with head/row pruning to achieve high structured pruning ratios with minimum accuracy degradation. Our empirical results show that for \bertbase, with \textapprox20\% of remaining weights, \OURS can achieve an accuracy that is comparable to the full model on QQP/MNLI/\squad, with up to \textapprox3.69x speedup. Our framework has been open sourced~\cite{codebase}.

Fast and Accurate Randomized Algorithms for Low-rank Tensor Decompositions

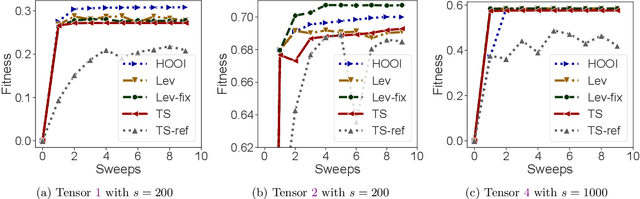
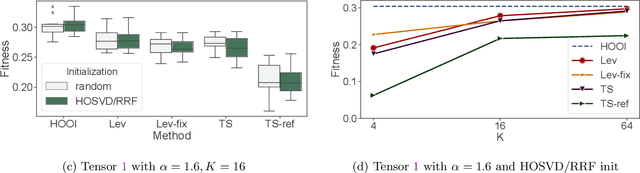
Low-rank Tucker and CP tensor decompositions are powerful tools in data analytics. The widely used alternating least squares (ALS) method, which solves a sequence of over-determined least squares subproblems, is inefficient for large and sparse tensors. We propose a fast and accurate sketched ALS algorithm for Tucker decomposition, which solves a sequence of sketched rank-constrained linear least squares subproblems. Theoretical sketch size upper bounds are provided to achieve $O(\epsilon)$-relative error for each subproblem with two sketching techniques, TensorSketch and leverage score sampling. Experimental results show that this new ALS algorithm, combined with a new initialization scheme based on randomized range finder, yields up to $22.0\%$ relative decomposition residual improvement compared to the state-of-the-art sketched randomized algorithm for Tucker decomposition of various synthetic datasets. This Tucker-ALS algorithm is further used to accelerate CP decomposition, by using randomized Tucker compression followed by CP decomposition of the Tucker core tensor. Experimental results show that this algorithm not only converges faster, but also yields more accurate CP decompositions.

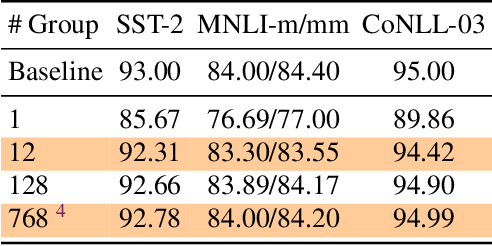
Q-BERT: Hessian Based Ultra Low Precision Quantization of BERT

Transformer based architectures have become de-facto models used for a range of Natural Language Processing tasks. In particular, the BERT based models achieved significant accuracy gain for GLUE tasks, CoNLL-03 and SQuAD. However, BERT based models have a prohibitive memory footprint and latency. As a result, deploying BERT based models in resource constrained environments has become a challenging task. In this work, we perform an extensive analysis of fine-tuned BERT models using second order Hessian information, and we use our results to propose a novel method for quantizing BERT models to ultra low precision. In particular, we propose a new group-wise quantization scheme, and we use a Hessian based mix-precision method to compress the model further. We extensively test our proposed method on BERT downstream tasks of SST-2, MNLI, CoNLL-03, and SQuAD. We can achieve comparable performance to baseline with at most $2.3\%$ performance degradation, even with ultra-low precision quantization down to 2 bits, corresponding up to $13\times$ compression of the model parameters, and up to $4\times$ compression of the embedding table as well as activations. Among all tasks, we observed the highest performance loss for BERT fine-tuned on SQuAD. By probing into the Hessian based analysis as well as visualization, we show that this is related to the fact that current training/fine-tuning strategy of BERT does not converge for SQuAD.

Inefficiency of K-FAC for Large Batch Size Training

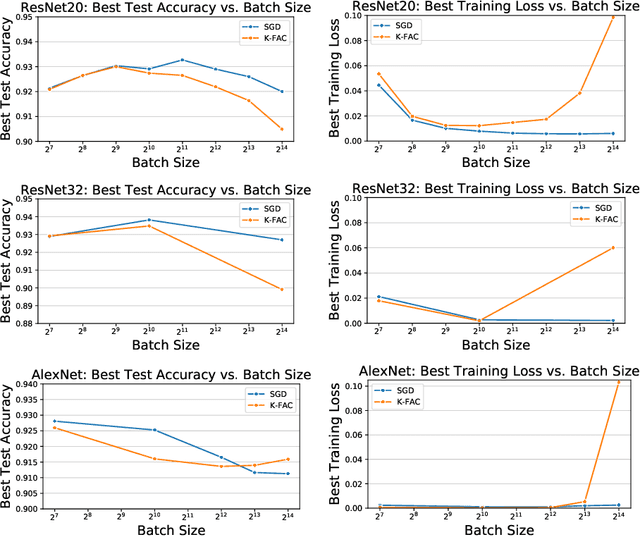
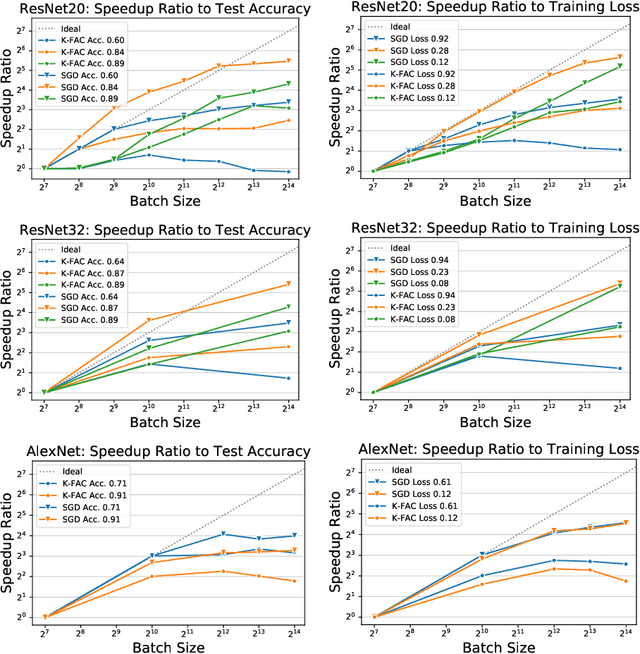
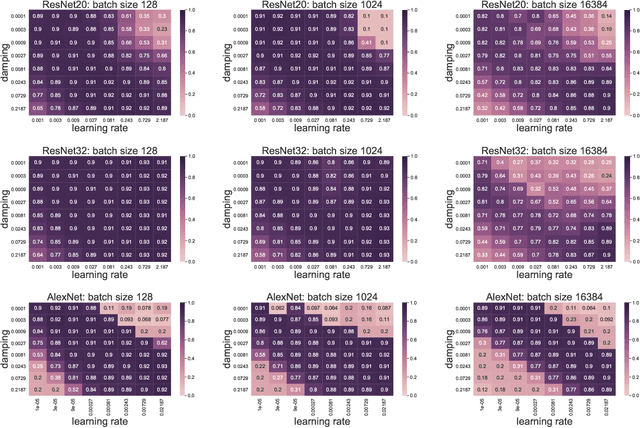
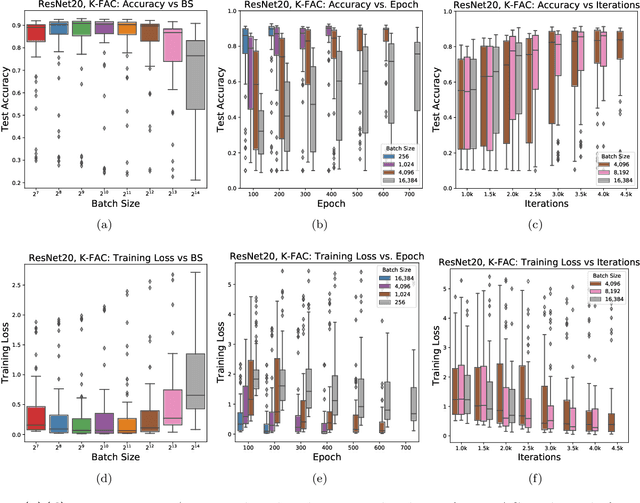
In stochastic optimization, large batch training can leverage parallel resources to produce faster wall-clock training times per epoch. However, for both training loss and testing error, recent results analyzing large batch Stochastic Gradient Descent (SGD) have found sharp diminishing returns beyond a certain critical batch size. In the hopes of addressing this, the Kronecker-Factored Approximate Curvature (\mbox{K-FAC}) method has been hypothesized to allow for greater scalability to large batch sizes for non-convex machine learning problems, as well as greater robustness to variation in hyperparameters. Here, we perform a detailed empirical analysis of these two hypotheses, evaluating performance in terms of both wall-clock time and aggregate computational cost. Our main results are twofold: first, we find that \mbox{K-FAC} does not exhibit improved large-batch scalability behavior, as compared to SGD; and second, we find that \mbox{K-FAC}, in addition to requiring more hyperparameters to tune, suffers from the same hyperparameter sensitivity patterns as SGD. We discuss extensive results using residual networks on \mbox{CIFAR-10}, as well as more general implications of our findings.