Inefficiency of K-FAC for Large Batch Size Training
Paper and Code
Mar 14, 2019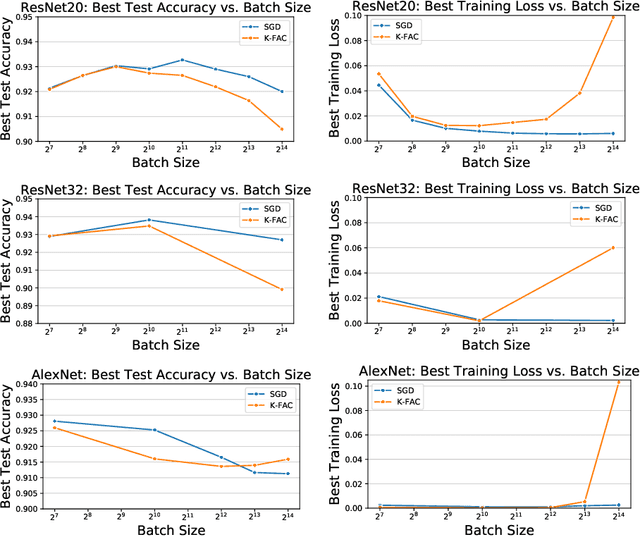
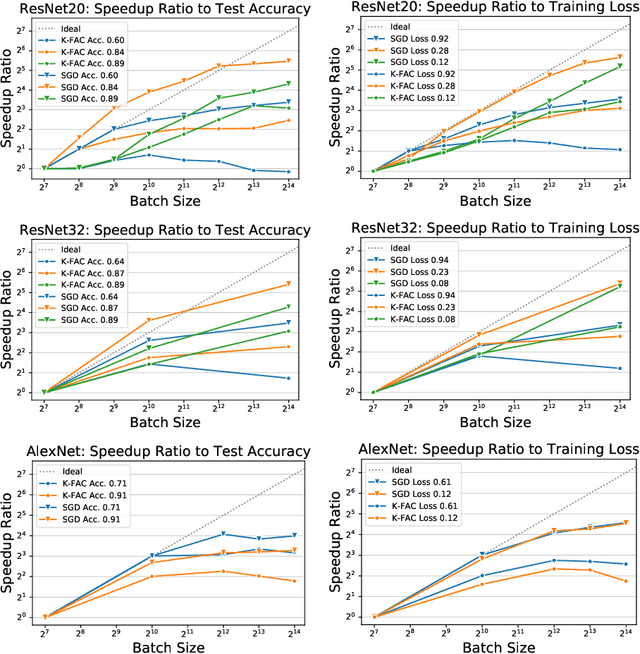
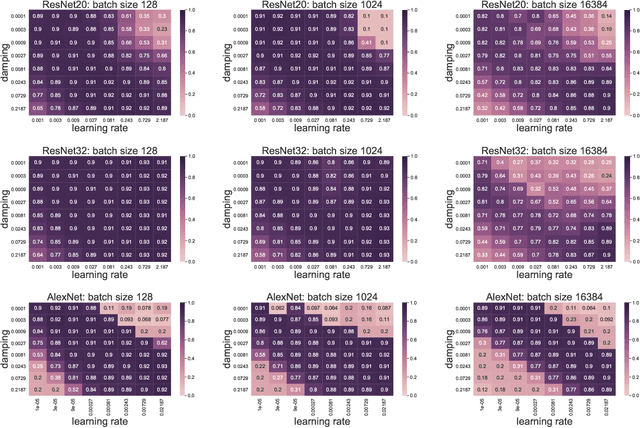
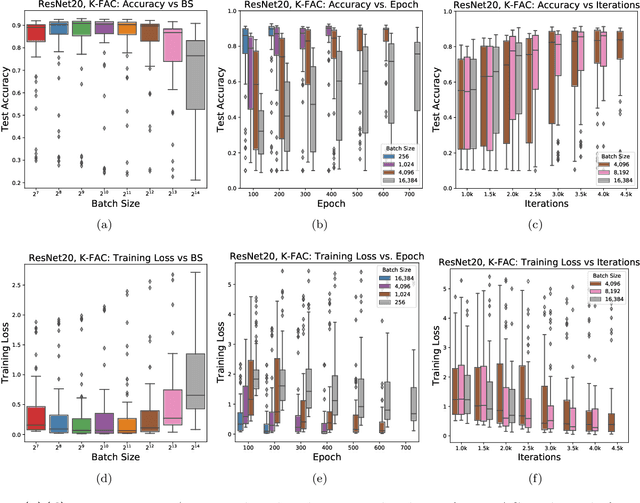
In stochastic optimization, large batch training can leverage parallel resources to produce faster wall-clock training times per epoch. However, for both training loss and testing error, recent results analyzing large batch Stochastic Gradient Descent (SGD) have found sharp diminishing returns beyond a certain critical batch size. In the hopes of addressing this, the Kronecker-Factored Approximate Curvature (\mbox{K-FAC}) method has been hypothesized to allow for greater scalability to large batch sizes for non-convex machine learning problems, as well as greater robustness to variation in hyperparameters. Here, we perform a detailed empirical analysis of these two hypotheses, evaluating performance in terms of both wall-clock time and aggregate computational cost. Our main results are twofold: first, we find that \mbox{K-FAC} does not exhibit improved large-batch scalability behavior, as compared to SGD; and second, we find that \mbox{K-FAC}, in addition to requiring more hyperparameters to tune, suffers from the same hyperparameter sensitivity patterns as SGD. We discuss extensive results using residual networks on \mbox{CIFAR-10}, as well as more general implications of our findings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge